数据结构之图(2-2)【邻接多重表】适用于无向图
邻接多重表(Adjacency Multilist)主要用于存储无向图。因为,如果用邻接表存储无向图,每条边的两个边结点分别在以该边
所依附的两个顶点为头结点的链表中,这给图的某些操作带来不便。例如,对已访问过的边做标记,或者要删除图中某一条边等,
都需要找到表示同一条边的两个结点。因此,在进行这一类操作的无向图的问题中采用邻接多重表作存储结构更为适宜。
邻接多重表的存储结构和十字链表类似,也是由顶点表和边表组成,每一条边用一个结点表示,其顶点表结点结构和边表结点
结构如图8.15 所示。


其中,顶点表由两个域组成,vertex 域存储和该顶点相关的信息firstedge 域指示第一条依附于该顶点的边;边表结点由六个域
组成,mark 为标记域,可用以标记该条边是否被搜索过;ivex 和jvex 为该边依附的两个顶点在图中的位置;ilink 指向下一条依
附于顶点ivex的边;jlink 指向下一条依附于顶点jvex 的边,info 为指向和边相关的各种信息的指针域。

例如,图8.16 所示为无向图8.1 的邻接多重表。在邻接多重表中,所有依附于同一顶点的边串联在同一链表中,由于每条边依附于两个顶
点,则每个边结点同时链接在两个链表中。可见,对无向图而言,其邻接多重表和邻接表的差别,仅仅在于同一条边在邻接表中用两个结
点表示,而在邻接多重表中只有一个结点。因此,除了在边结点中增加一个标志域外,邻接多重表所需的存储量和邻接表相同。在邻接多
重表上,各种基本操作的实现亦和邻接表相似。
代码如下:
1 #include "stdafx.h" 2 #include<iostream> 3 using namespace std; 4 5 typedef int VertexType; 6 #define MAX_VERTEX_NUM 20 7 typedef enum{unvisited,visited} VisitIf; 8 typedef struct EBox 9 { 10 VisitIf mark; //访问标记 11 int ivex, jvex; //该边依附的两个顶点的位置 12 struct EBox *ilink, *jlink;//分别指向依附的两个顶点的下一条边 13 int info; //该边信息指针,可指向权值或其他信息 14 }EBox; 15 typedef struct VexBox 16 { 17 VertexType data; 18 EBox *firstarc; //指向第一条依附改点的边 19 }VexBox; 20 typedef struct 21 { 22 VexBox adjmulist[MAX_VERTEX_NUM]; 23 int vexnum, arcnum; //无向图的当前顶点数和边数 24 }AMLGraph; 25 26 int LocateVex(AMLGraph G, VertexType v)// 初始条件:无向图G存在,v和G中顶点有相同特征 27 // 操作结果:若G中存在顶点v,则返回该顶点在无向图中位置;否则返回-1 28 { 29 for (int i = 0; i < G.vexnum; i++) 30 if (G.adjmulist[i].data == v) 31 return i; 32 return -1; 33 } 34 35 void CreateGraph(AMLGraph &G)//采用邻接多重表构建无向图G 36 { 37 VertexType v1, v2; 38 cout << "请输入总顶点数和总边数(用空格隔开):"; 39 cin >> G.vexnum >> G.arcnum; 40 cout << "输入顶点" << endl; 41 for (int i = 0; i < G.vexnum; i++)//构造顶点向量 42 { 43 cin >> G.adjmulist[i].data ; 44 G.adjmulist[i].firstarc = NULL; 45 } 46 cout << "请输入每条边的两个端点以及权值:" << endl; 47 for (int k = 0; k < G.arcnum; k++)//构造表结点链表 48 { 49 EBox *p = new EBox;; 50 cin >> v1 >> v2 >>p->info; 51 int m = LocateVex(G, v1);//一端 52 int n = LocateVex(G, v2);//另一端 53 p->mark = unvisited; 54 p->ivex = m; //插在一端表头 55 p->ilink = G.adjmulist[m].firstarc; 56 G.adjmulist[m].firstarc = p; 57 p->jvex = n; //插在另一端表头 58 p->jlink = G.adjmulist[n].firstarc; 59 G.adjmulist[n].firstarc = p; 60 } 61 } 62 63 void MarkUnvizited(AMLGraph G)//置边的访问标记为未被访问 64 { 65 int i; 66 EBox *p; 67 for (i = 0; i<G.vexnum; i++) 68 { 69 p = G.adjmulist[i].firstarc; 70 while (p) 71 { 72 p->mark = unvisited; 73 if (p->ivex == i) 74 p = p->ilink; 75 else 76 p = p->jlink; 77 } 78 } 79 } 80 81 82 void display(AMLGraph G)//输出无向图的邻接多重表 83 { 84 EBox *p; 85 MarkUnvizited(G); 86 cout << "无向图有" << G.vexnum << "个顶点,分别为:"; 87 for (int i = 0; i < G.vexnum; i++) 88 { 89 cout << G.adjmulist[i].data << " "; 90 91 } 92 cout << endl; 93 for (int i = 0; i < G.vexnum; i++) 94 { 95 cout << "和" << G.adjmulist[i].data << "有关的边:"; 96 p = G.adjmulist[i].firstarc; 97 while (p) 98 { 99 if (p->ivex == i) // 边的m端与该顶点有关 100 { 101 if (p->mark) 102 { 103 cout << G.adjmulist[i].data <<" "<< G.adjmulist[p->jvex].data<<" "; 104 p->mark = visited; 105 if (p->info) 106 cout << "权值:" << p->info << ". "; 107 } 108 p = p->ilink; 109 } 110 else // 边的n端与该顶点有关 111 { 112 if (!p->mark) 113 { 114 cout << G.adjmulist[p->ivex].data <<" "<< G.adjmulist[i].data<<" "; 115 p->mark = visited; 116 if (p->info) 117 cout << "权值:" << p->info << ". "; 118 } 119 p = p->jlink; 120 } 121 } 122 cout << endl; 123 } 124 } 125 126 int main() 127 { 128 AMLGraph MG; 129 CreateGraph(MG); 130 display(MG); 131 return 0; 132 }
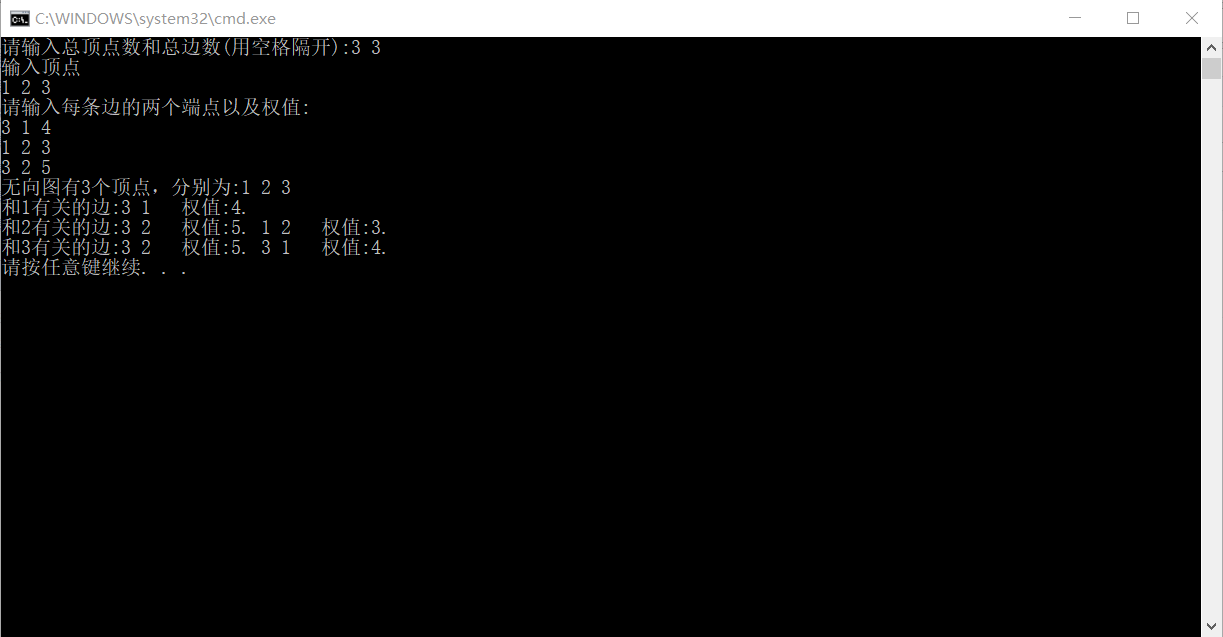
输出结果:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号