数据结构之图（1）【邻接矩阵、邻接表】

邻接矩阵创建无向网：

图的邻接矩阵（Adjacency Matrix)存储方式是用两个数组来表示图。一个一维的数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

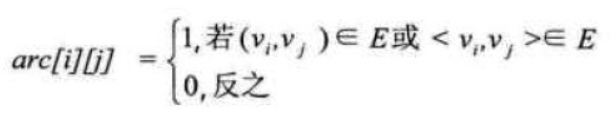
我们来看一个实例，图7-4-2的左图就是一个无向图。

我们再来看一个有向图样例，如图7-4-3所示的左图。

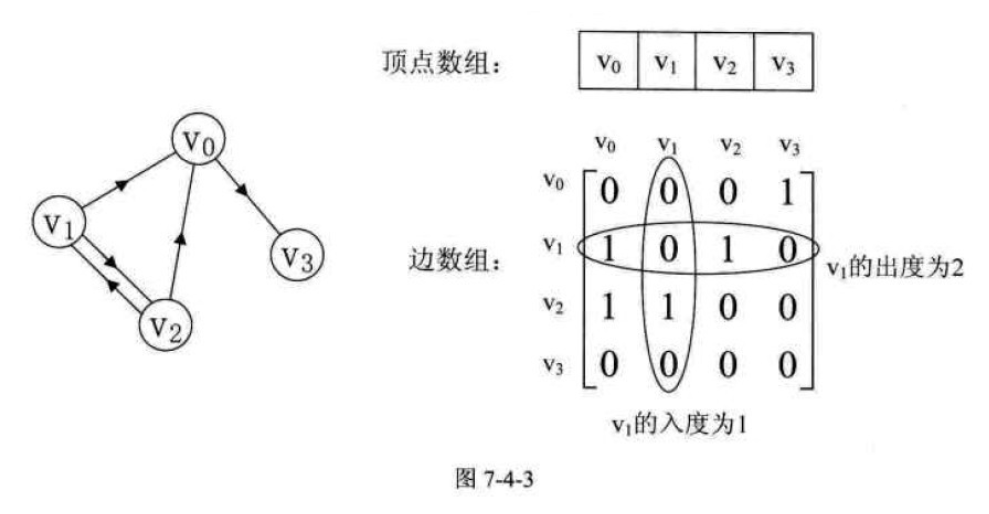
在图的术语中，我们提到了网的概念，也就是每条边上都带有权的图叫做网。那些这些权值就需要保存下来。

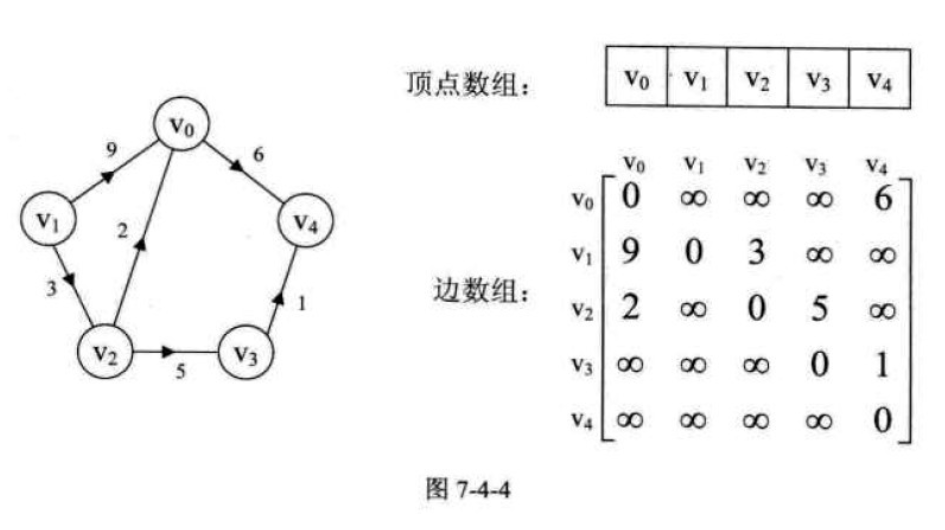
设图G是网图，有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

如图7-4-4左图就是一个有向网图。

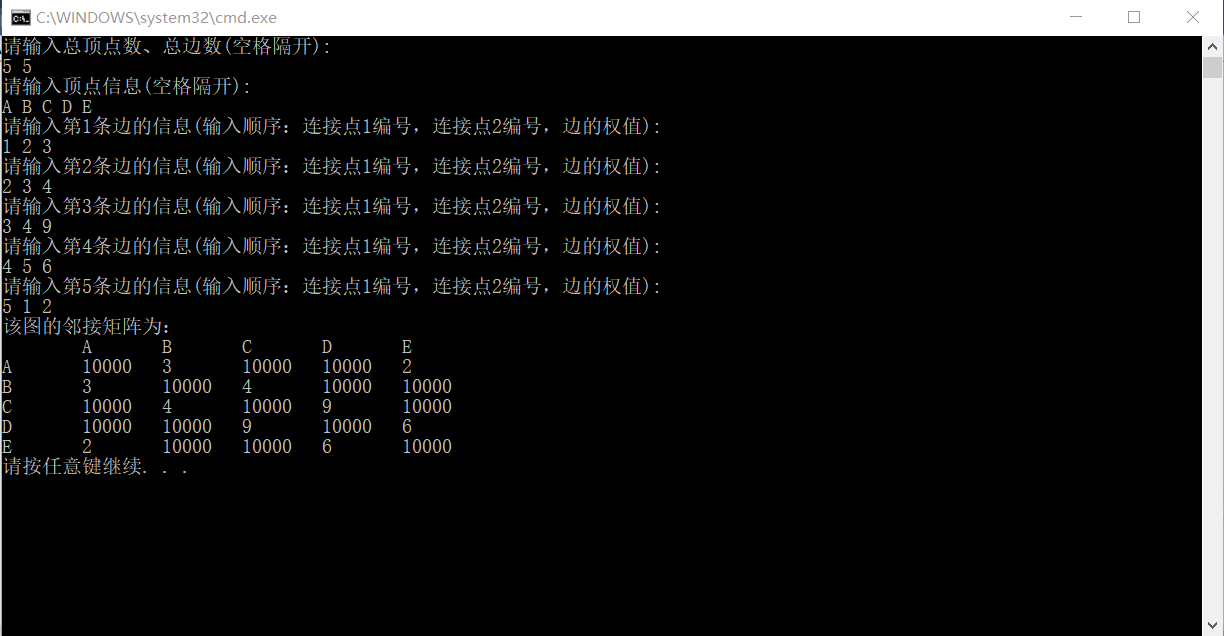
下面示例无向网图的创建代码：

#include "stdafx.h"
#include<iostream>
#define MaxInt 10000                   //表示权值的无穷
#define MVNum 100                      //最大顶点数，应由用户定义
typedef char VerTexType;               //假设顶点数据类型为字符型
typedef int ArcType;                   //假设边的权值类型为整形
using namespace std;
typedef struct
{
    VerTexType vexs[MVNum];            //顶点表
    ArcType arcs[MVNum][MVNum];        //邻接矩阵
    int vexnum, arcnum;                //图的当前点数和边数
}AMGraph;

void CreateUDN(AMGraph &G)             //采用邻接矩阵表示法，创建无向网&G
{
    int i, j, w;
    cout << "请输入总顶点数、总边数(空格隔开):" << endl;
    cin >> G.vexnum >> G.arcnum;       //输入总顶点数、总边数
    cout << "请输入顶点信息(空格隔开):" << endl;
    for (i = 0; i < G.vexnum; i++)     //依次输入点的信息
    {
        cin >> G.vexs[i];
    }
    for (i = 0; i < G.vexnum; i++)     //初始化邻接矩阵，编的权值均为极大值MaxInt
        for (j = 0; j < G.vexnum; j++)
            G.arcs[i][j] = MaxInt;

    for (int k = 0; k < G.arcnum; k++) //构造邻接矩阵
    {
        cout << "请输入第" << k + 1 << "条边的信息(输入顺序：连接点1编号，连接点2编号，边的权值):" << endl;
        cin >> i >> j >> w;            //输入一条边依附的顶点及权值
        G.arcs[i - 1][j - 1] = w;      
        G.arcs[j - 1][i - 1] = G.arcs[i - 1][j - 1];
    }
}

void coutAMGraph(AMGraph &G)           //无向网的输出
{
    int i, j;
    cout << "该图的邻接矩阵为：" << endl;
    cout << "\t";
    for (i = 0; i < G.vexnum; i++)
        cout << G.vexs[i] << "\t";
    cout << endl;
    for (i = 0; i < G.vexnum; i++)
    {
        cout << G.vexs[i] << "\t";
        for (j = 0; j < G.vexnum; j++)
        {
            cout << G.arcs[i][j] << "\t";
        }
        cout << endl;
    }
}
int main()
{
    AMGraph MG;
    CreateUDN(MG);
    coutAMGraph(MG);
    return 0;
}

输出结果:

邻接表创建无向网:

邻接表（Adjacency List） 是图的一种链式存储结构，在邻接表中，对图中每个顶点建立一个单链表，第i个单链表中的节点表示依附于顶点Vi的边（对有向图是以顶点Vi为尾的弧）。每个节点由3个域组成，其中邻接点域（adjvex）指示与顶点vi邻接的点在图中的位置，链域（nextarc）指示下一条边或弧的节点；数据域（info）存储和边或弧相关的信息，如权值等。每个链表上附设一个表头节点。在表头节点中，除了设有链域（firstarc）指向链表中的第一个节点之外，还设有存储顶点Vi的名或者其他有关信息的数据域（data）。

如图：

头节点（存储顶点信息）

表（边）节点（存储两个顶点之间边的信息）

这些表头节点（可以链相接）通常以顺序结构的形式存储，以便随机访问任一个顶点的链表。

 

上面这一段是严蔚敏版数据结构那本书中对用邻接表法构建图的介绍，说的过于理论化，我第一次看的时候也是不知所云，但是仔细阅读，并且阅读了书中的伪代码，便明白了作者的意思。现在做出简要总结：

在构建图时，需要两个结构体，一个存储图中节点的信息，便是上面介绍的头节点，一个是两个节点之间边的信息，便是上面的表（边）节点。 采用一个一维数组存储头结点信息，然后为每个头结点建立一个链表，让头结点作为这个链表的表头节点（具体实现方法便是让头结点内的指针firstarc 指向链表的首地址），链表中存储的正是和这个头结点相关联的表节点（边的信息），这些边都是尾部和头结点相连。表节点中的adjvex存储的是与这条边关联的另一个头结点在数组中的索引（边的箭头所关联的头节点），表节点中的nextarc则是存储的该链表表头相关联的另一条边的信息。

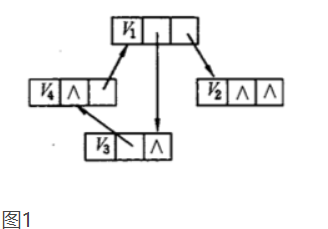
下图是上图的邻接表：

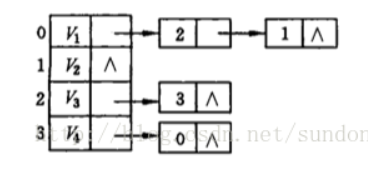
图2

以第一行为例：V1是图中的头结点，V1后面的链表是所有与V1相连的边

此处需要普及一个概念：我们平时口语所说的边，例如上面的图1中V1 指向 V2的那条边，在图论里面成为“弧”，对于弧来说V1叫“弧尾”，V2是该弧的“弧头”。（虽然不知道名字的来源故事，但是至少人家是专业术语，说出去，让人一听，感觉好高大上的样子，装逼必备利器）。

下面是代码：

#include "stdafx.h"
#include<iostream>
#include<string>
using namespace std;
#define MVNum 100                      //最大顶点值
#define ERROR 1 
typedef char VerTexType;
typedef struct ArcNode                 //边结点
{
    int adjvex;                        //改变所指向的顶点的位置
    struct ArcNode *nextarc;           //指向下一条边的指针
    string info;                       //和边相关的信息
}ArcNode;
typedef struct VNode                   //顶点信息
{                 
    VerTexType data;                   
    ArcNode *firstarc;                 //指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum];                //AdList表示邻接表类型
typedef struct                         //邻接表
{
    AdjList vertices; 
    int vexnum, arcnum;                //图的当前顶点数和边数
}ALGraph;

int LocateVex(ALGraph &G, char &v1)    //定位函数   
{
    int i;
    for (i = 0; i < G.vexnum; i++)
    {
        if (G.vertices[i].data == v1)
            return i;
    }
    if (i >= G.vexnum)
        return ERROR;
    else
        return 0;
}
void CreateUDG(ALGraph &G)             //创建无向图
{
    ArcNode *p1, *p2;
    int i, j, k;
    char v1, v2;
    cout << "请输入图的顶点数、弧数：" << endl;
    cin >> G.vexnum >> G.arcnum;       //输入总顶点数，总边数
    cout << "请输入顶点：" << endl; 
    for (i = 0; i < G.vexnum; i++)
    {
        cin >> G.vertices[i].data;     //输入顶点值
        G.vertices[i].firstarc = NULL; //初始化表头结点的指针域为NULL
    }
    for (k = 0; k < G.arcnum; k++)     
    {
        cout << "请输入弧尾和弧头：";
        cin >> v1 >> v2;               //输入各边，构造邻接表
        i = LocateVex(G, v1);
        j = LocateVex(G, v2);
        p1 = new ArcNode;              //生成一个新结点*p1
        p1->adjvex = j;                //邻接点序号为j
        p1->nextarc = G.vertices[i].firstarc;
        G.vertices[i].firstarc = p1;
        p2 = new ArcNode;
        p2->adjvex = i;
        p2->nextarc = G.vertices[j].firstarc;
        G.vertices[j].firstarc = p2;
    }
    cout << "图构建成功！" << endl;
}

void coutUDG(ALGraph G)                //输出函数
{
    int i, j;
    cout << "输出为:" << endl;
    for (i = 0; i<G.vexnum; i++)
    {
        cout << i;
        ArcNode *p;
        p = G.vertices[i].firstarc;
        while (p != NULL)
        {
            cout << "-> " << p->adjvex;
            p = p->nextarc;
        }
        cout << endl;
    }
}
int main()
{
    ALGraph MG;
    CreateUDG(MG);
    coutUDG(MG);
    return 0;
}

 

输出结果:

 

今天就先到这里啦，下一篇再写十字链表和邻接多重表哈！