字典树模版
老实说,我自认为字典树是我目前学了四种字符串处理的算法当中最好理解而且最可爱的一个算法
1463: [视频]【字典树】统计前缀
时间限制: 1 Sec 内存限制: 128 MB
提交: 215 解决: 117
[提交] [状态] [讨论版] [命题人:admin]题目描述
【题意】
给出很多个字符串(只有小写字母组成)和很多个提问串,统计出以某个提问串为前缀的字符串数量(单词本身也是自己的前缀).
【输入格式】
输入n,表示有n个字符串(n<=10000)
接下来n行,每行一个字符串,字符串度不超过10
输入m,表示有m个提问(m<=100)
第二部分是一连串的提问,每行一个提问,每个提问都是一个字符串.
【输出格式】
对于每个提问,给出以该提问为前缀的字符串的数量.
【样例输入】
5
banana
band
bee
absolute
acm
4
ba
b
band
abc
【样例输出】
2
3
1
0字典树练习:
HDU1251(本题原版)
HDU1075
HDU1800
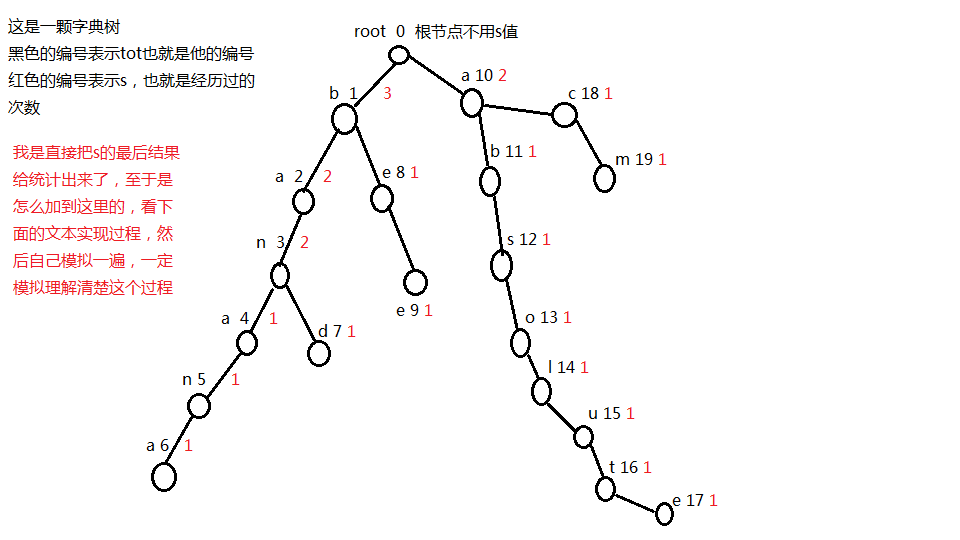
字典树是用来保存字符的一棵树
如图
有一个root,是一个虚根,设为0号点,保存每个字符串的第一个字母
样例:
5
banana
band
bee
absolute
acm
4
ba
b
band
abc然后接下来看到banana这个字符串
处理第一个字符“b”,我们先问根节点,b的孩子是否存在,b的孩子是什么意思呢?
其实在字典树上面,每一个节点都有26个孩子(相对这题而言),第一个孩子是a,第二个是b,依次类推然后问根节点b的孩子存不存在,不存在就增加一条边,也就是把孩子变成存在的,这个点就代表b,但是我们总要赋予一个编号吧
所以我们定义一个变量tot,表示整棵树有多少个点,tot一开始等于0,代表这棵树上面是没有点的,而虚根不算是一个点,只是用来统计单词第一个字符而已,这个时候,增加了一条边,b出现了,所以tot++,然后b的编号就为tot,也就是1
但是还没有结束,这个时候就到字符串的第二个字母,a
这个时候就不可以从虚根开始问了,而是要从b这里问他的孩子,不存在就增加一条边,把a孩子设为存在,tot++,编号为2然后就是这样一直往下问,先建好第一个单词
然后我们就要建第二个单词了band,第一个字母“b”,问虚根,显然是存在的,因为我们刚才增加了,存在就不用在建一个点,然后直接问b的孩子,a存在,然后问a的孩子,n存在,然后往下问n的孩子,d是否存在,这个时候d是不存在的,然后就建一个d点,编号为7(前面增加到6)
然后我们一直按照这种方式处理到bee这个字符串
然后建开头为a的话就在旁边新开一个点就可以了,毕竟一个节点最大可能是拥有26个孩子节点
然后我们就非常成功的把字符串安装在一棵树上面了
这个时候我们根据题目要求的,我们可以把每个点都给一个s值,表示每次建一个字符串的时候,所经历的点的次数,比如建banana时,
先建b,s=1,因为我们建的时候,经历了root这条边一次
然后剩下的这个anana的s都等于1,因为他们都是重新组建的,所以s=1然后第二个单词band
首先是b,然后这个时候b经历了第二次,所以这个时候b的s=2,a的s=2,n的s=2,d的s=1然后到bee
首先是b,经历了三次,b的s=3,这个过程可以在我们建字典树的时候同步完成
接下来就到提问了,提问以该串为前缀的字符串的数量
然后我们就很懵逼了,建了一棵树又有什么用呢?
别忘了我们之前是定义了一个变量s的,这个s在这一步的作用就非常大了
我们用s来记录之后,我们就看可以很轻松的得到答案,为什么呢?
其实字典树上面的每一个点,到虚根root所经历的每个点都可以独立成为一个单词,
比如说ban,这个是我们在经历的时候构建的独立的一个单词,但是你会发现至少在字典树里面是没有和他完全相同的单词的,所以可以说字典树上面的每一个点代表着一个单词然后可能有人会觉得很奇怪,为什么一定呢?你这样想啊,如果我们找到了一个前缀为ban的单词,这个时候你如果还想找一个一模一样的,一定会和ban重合,那么不就是归根到底只有一个咯
比如说我们找以ba为前缀的字符串的数量,直接找肯定太麻烦了
我们就直接在树上面找,找b,然后到a,发现a是我们提问串的最后一个单词,然后发现a的s=2,说明有两个经历过,所以可以肯定的输出,因为这两个字符串的前缀一定有ba,因为我们是从前往后建的这一棵树,所以从root下来,所经历的点就代表了他的前缀,所经历的每一个点所构成的单词都是他的前缀
这样就很简单了,我们只要在字典树上面找提问串,找到最后一个字母,把这个字母所对应的s输出就可以了
但是如果我们找着找着发现提问串当中有一个字母没有办法对应上来的话,没有出现过,说明不可以成为任何一个字符串的前缀,这个时候就直接return 0,不然就继续找,找到最后就直接输出
是不是特别的好理解,我相信你们看完上面的介绍之后,已经可以把大致的模版打出来了,build_tree和solve函数,以及一个结构体,就完成了,还是看一下代码实现吧
(注释版,这个其实看不看都没关系,因为你看了非注释版估计都懂了,但是如果真的不懂就看一下吧)

1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<cmath> 6 #include<iostream> 7 using namespace std; 8 char a[100010]; 9 int ans,tot;/*ans记录答案,tot记录编号*/ 10 struct node 11 { 12 int s,cnt[30];/*cnt表示孩子节点,(一共26个)s表示经历的次数*/ 13 node() 14 { 15 s=0;/*刚开始没有经历过*/ 16 memset(cnt,-1,sizeof(cnt));/*初始化没有孩子*/ 17 } 18 }tr[100010]; 19 void build_tree(int root)/*建树*/ 20 { 21 int x=root; int len=strlen(a+1); 22 for(int i=1;i<=len;i++) 23 { 24 int y=a[i]-'a'+1;/*这样之后就保证y是1~26*/ 25 if(tr[x].cnt[y]==-1) tr[x].cnt[y]=++tot;/*没有这个孩子节点,就增加一个编号*/ 26 x=tr[x].cnt[y]; tr[x].s++;/*跳到当前处理的,同时处理s值*/ 27 } 28 } 29 void solve(int root) 30 { 31 int x=root; int len=strlen(a+1); 32 for(int i=1;i<=len;i++) 33 { 34 int y=a[i]-'a'+1; 35 if(tr[x].cnt[y]==-1) {ans=0;return ;}/*没有这个点的话,直接返回0*/ 36 x=tr[x].cnt[y]; 37 } 38 ans=tr[x].s;/*返回答案*/ 39 } 40 int main() 41 { 42 int n,m; scanf("%d",&n); 43 for(int i=1;i<=n;i++) 44 { 45 scanf("%s",a+1); 46 build_tree(0); 47 } 48 scanf("%d",&m); 49 for(int i=1;i<=m;i++) 50 { 51 scanf("%s",a+1); 52 ans=0; solve(0); /*ans每一次都要归零*/ 53 printf("%d\n",ans); 54 } 55 return 0; 56 }

1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<cmath> 6 #include<iostream> 7 using namespace std; 8 char a[100010]; 9 int ans,tot; 10 struct node 11 { 12 int s,cnt[30]; 13 node() 14 { 15 s=0; 16 memset(cnt,-1,sizeof(cnt)); 17 } 18 }tr[100010]; 19 void build_tree(int root) 20 { 21 int x=root; int len=strlen(a+1); 22 for(int i=1;i<=len;i++) 23 { 24 int y=a[i]-'a'+1; 25 if(tr[x].cnt[y]==-1) tr[x].cnt[y]=++tot; 26 x=tr[x].cnt[y]; tr[x].s++; 27 } 28 } 29 void solve(int root) 30 { 31 int x=root; int len=strlen(a+1); 32 for(int i=1;i<=len;i++) 33 { 34 int y=a[i]-'a'+1; 35 if(tr[x].cnt[y]==-1) {ans=0;return ;} 36 x=tr[x].cnt[y]; 37 } 38 ans=tr[x].s; 39 } 40 int main() 41 { 42 int n,m; scanf("%d",&n); 43 for(int i=1;i<=n;i++) 44 { 45 scanf("%s",a+1); 46 build_tree(0); 47 } 48 scanf("%d",&m); 49 for(int i=1;i<=m;i++) 50 { 51 scanf("%s",a+1); 52 ans=0; solve(0); 53 printf("%d\n",ans); 54 } 55 return 0; 56 }