EXKMP模版
这道题目折腾了我好一会啊,出于尊重我要先放我们师兄的博客
1178: [视频]EXKMP模版:最长共同前缀长度
时间限制: 1 Sec 内存限制: 128 MB
提交: 180 解决: 123
[提交] [状态] [讨论版] [命题人:admin]题目描述
【题目描述】
给出模板串A和子串B,长度分别为lenA和lenB,要求在线性时间内,对于每个A[i](1<=i<=lenA),求出A[i..lenA]与B的最长公共前缀长度
【输入格式】
输入A,B两个串,(lenB<=lenA<=1000000)【输出格式】
输出lenA个数,表示A[i...lenA]与B的最长公共前缀长度,每个数之前有空格【样例输入】
aabbabaaab
aabb
【样例输出】4 1 0 0 1 0 2 3 1 0
我们就引入了一个叫EXKMP的东西,接下来看下面的解释
一个非常重要的提醒,你们看在博客的时候遇到图一定要拖出来放大看,因为颜色在模糊处会重合
首先看到EXKMP,是不是很容易联想到我们上一次提到的KMP呢?回忆一下KMP
KMP:p[ ]表示以结尾为首和以开头为首的最长公共字串 (p[ ]是作为KMP的一个重要数组)
EXKMP:extend[ ]表示以i为首和以开头为首的最长公共前缀长度 (extend[ ]是作为EXKMP的一个重要数组)
目的:st[1~extend[i]]=st[i~i+extend[i]-1] (st表示原来的字符串)
extend[1]=len,因为以第一个字母为首的最长公共前缀就是整个字符串我先在这里讲清楚,extend数组的意义一定要记住,因为这个东西在后面的证明当中是非常非常重要的
很好我们现在已经把EXKMP当中的最基础的比较重要的给讲清楚了,要注意一下,EXKMP和KMP一样也是对单串进行处理
显然作为一个非常害人的算法,怎么可能就这么一点东西呢?
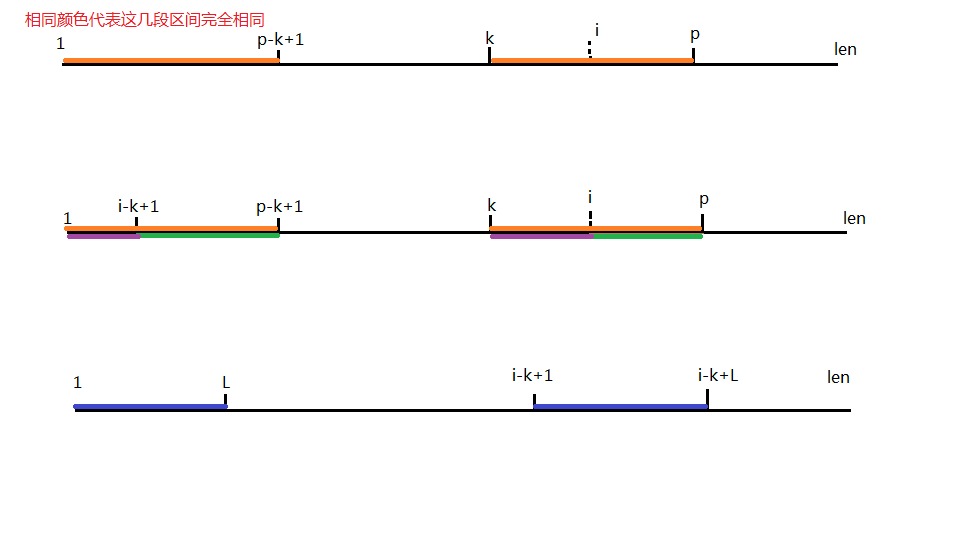
k表示当前搜索过的范围以为能到达的最远编号
p表示k+extend[k]-1,(也就是说k+extend[k]-1最大)
p记录以k为首和以开头为首的最长公共前缀长度,k+最长公共前缀长度后所到达的编号因为st[1~extend[k]]=st[k~p] (中间的波浪线表示某到某)
化简来说就是 st[1~extend[k]]= st[k~k+extend[k]]-1] 这个我相信是没有任何问题的
所以extend[k]-1+1=p-k+1
extend[k]=p-k+1
所以 st[1~p-k+1]=st[k~p]这个是真的很好看出来,不过我还是在这里说清楚,这个p的含义很重要,p-k+1在后面也有比较大的用处
定义L=extend[i-k+1]
st[i-k+1~i-k+1+L-1]=st[i-k+1~i-k+L] (向右延伸L的长度)
st[i-k+1~i-k+L]=st[1~L] 这个的话可能需要感性理解一下这个延伸的含义,就是说我们如果是相同的区间,延伸相同的长度,那么延伸之后也是相同的
然后把p,k,L,i合在一起
因为L的不定性,我们就要考虑 i-k+L 和 p-k+1 的大小 (分情况讨论)
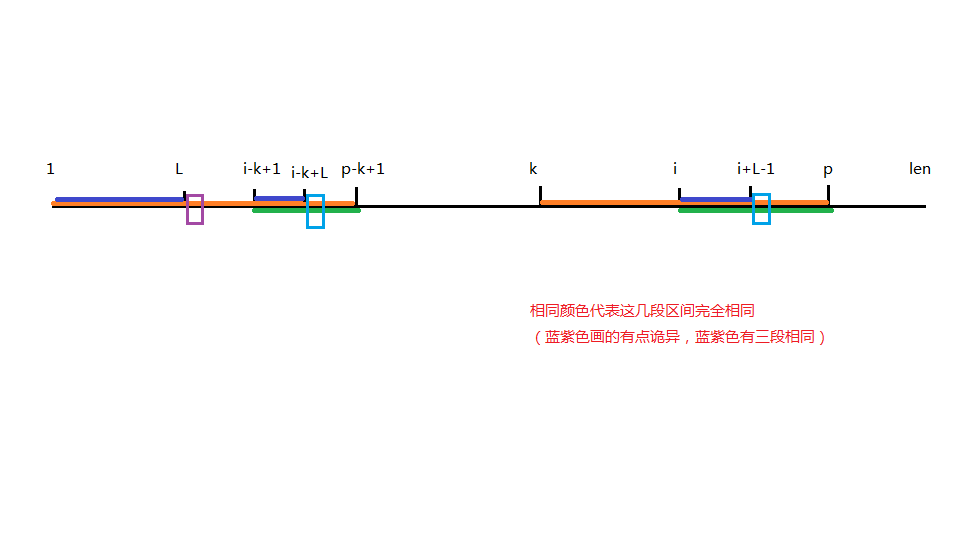
1.i-k+L<p-k+1
从图中我们可以看到
因为st[1~L]=st[i-k+1~i-k+L]
st[i-k+i~p-k+1]=st[i~p]
所以在st[i~p]当中一定含有一段从i开始和 st[1~L]是完全相同的,所以 st[i~i+L-1] 是与之完全相同的 (蓝紫色位置)
因为 st[i-k+1~p-k+1]=st[i~p]
又因为 i-k+L<p-k+1
所以我们得到 st[i-k+L+1]=st[i+L] (蓝色位置)
又因为extend[i-k+ 1]的定义
所以 st[L+1] (紫色位置)!=st[i-k+L+1]
因为 st[i-k+L]=st[i+L-1] -> st[i-k+L+1]=st[i+L]
又因为 st[L+1]!=st[i-k+L+1]
所以可以得到 : st[i+L]!=st[L+1] ,(其实就是证明了紫色和第二个黄色是不匹配的)
那么extend[i]就直接等于L了(最大字串前缀长度,不匹配就为原来匹配的最大值)所以第一种情况就是直接记录L
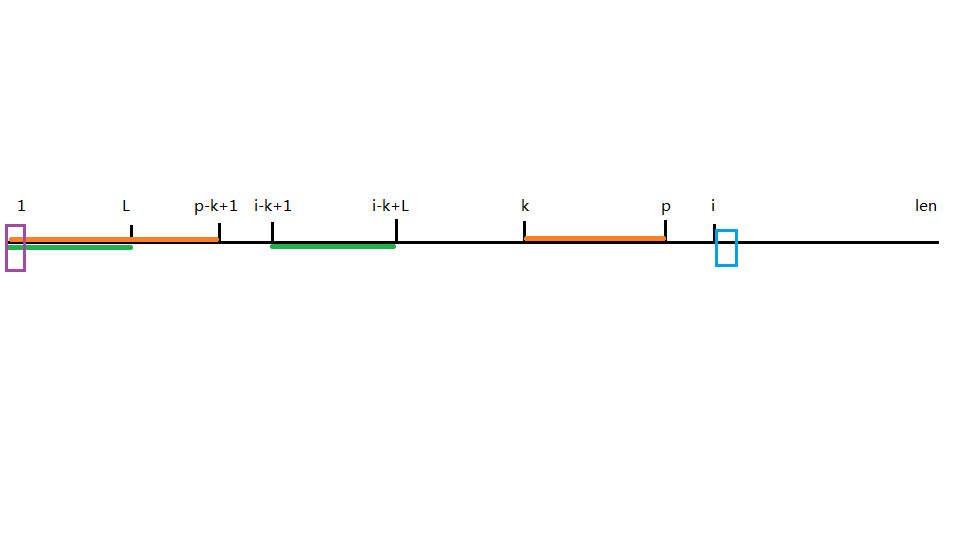
2.i-k+L>p-k+1
从图中我们可以看到因为 st[1~L]=st[i-k+1~i-k+L] (蓝紫色)
又因为 i-k+L>p-k+1所以在 st[1~L]中肯定含有一段和 st[i-k+1~p-k+1] 完全相同(绿色)
因为extend[k]的意义
所以st[p+1]!=st[p-k+2] (第二个紫色和黄色位置)
不然的话橙色的长度应该往后延伸,但是并没有,因为extend的定义确定了他的最长公共字串前缀
又因为st[1~L]=st[i-k+1~i-k+L]
所以st[p-i+2] (第一个紫色位置)=st[p-k+2]
因为我们绿色部分相同,而且蓝紫色部分也相同,那就证明我们各自往后一格也是相同的。
那么st[p-i+2]!=st[p+1],所以extend[i]就等于p-i+1
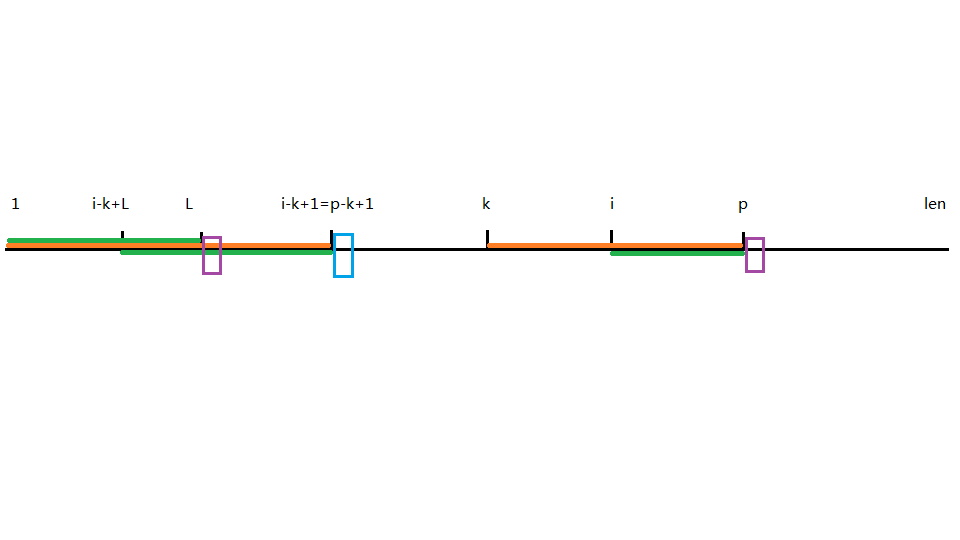
3.i-k+L=p-k+1
从图中我们可以看到
因为st[i-k+1~i-k+L]=st[1~L]
st[i-k+1~p-k+1]=st[i~p]
又因为 i-k+L=p-k+1
所以 st[1~L]=st[i-k+1~p-k+1] (可换成i-k+L) =st[i~p] (绿色)
那么由于 extend[i-k+1] 和 extend[k] 的意义表达
可以得到 st[L+1]!=st[i-k+L+1](第一个紫色不等于蓝色)
st[i-k+L+1]!=st[p+1]
但是我们不能确定 st[L+1] 和 st[p+1] 是否相同,我们只能确定从i开始和
从1开始有 p-i+1这么长的公共前缀,但并不一定是最长的那么我们就设一个变量j=p-i+1,表示当前从i开始和从1开始的公共前缀长度
由于上面这句话,可以直接从st[j+1] 和 st[i+j] 来累加j的值来得出最长的公共前缀(直接一个一个往后匹配)
xixixixi.细节上面的问题
因为p是一个不定的数(由k和extend[k]来决定)
所以说p-i+1是有可能为负数的
那么第二种情况显然不对
公共前缀肯定不可以为负数,最小也只能是0
所以我们就要想要在第二种情况下去 p-i+1和0 的最大值
但是这是不对的
因为我们如果直接粗鲁的求最大值,那么我么直接就是0了,但是我们不能判断i+1这个格子(蓝色) 和 1+1这个格子(紫色)是否相同的情况下直接输出0,自然是有问题的从图中我们可以看到,因为p-i+1是负数
所以上面所有的条件都用不了
因为i对后面的字符没有作任何的计算
但这个时候是绝对不可以肯定st[1] 和 st[i]是不同的(也就是最长公共前缀为0)
所以我们需要从st[1]和st[i]开始判断后面的字符是否相同,
然后我们知道在第二种情况的时候也出现了一个个往后面匹配,
所以我们把第二种情况和第三种情况归纳为一种情况但是....
这种做法仅仅是匹配单个字符串的,但是这个时候我们要把A串和B串一起匹配
这个时候我们可以就是一开始定一个数组ex[i],表示从i-lena与B的最长公共前缀长度
一开始1不能直接等于len
所以我们直接从1开始到while到后面发现不同的时候就退出,
然后取前面和他一样长的,也就是说:我们的ex是通过一个个匹配得出来的
一直到这里,我们对单串的EXKMP的处理也就结束了,这个东西的话,还是自己手动画图模拟一遍,不难懂但是一定要很细心很细心
接下来看代码的实现
(注释版:我建议就看注释版先,因为我们知道细节的存在,让我们的代码变得如此“可爱”)

1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<cmath> 6 #include<iostream> 7 char sa[1000010],sb[1000010]; 8 int ex[1000010],p[1000010],lena,lenb; 9 /*p[]表示b串单独匹配自己的字符串,也就是extend数组 10 ex[]表示把a串和b串互相匹配*/ 11 inline void EXKMP() 12 { 13 p[1]=lenb;/*整个字符串长度*/ 14 int i=1,k; 15 while(sb[i]==sb[i+1] && i+1<=lenb) i++;/*通过这种方式求出p[2]*/ 16 p[2]=i-1; k=2;/*k表示当前搜索过的范围以为能到达的最远编号*/ 17 int tp,l;/*tp表示k+extend[k]-1,tp记录以k为首和以开头为首的最长公共前缀长度,k+最长公共前缀长度后所到达的编号*/ 18 for(int i=3;i<=lenb;i++) 19 { 20 tp=k+p[k]-1; l=p[i-k+1];/*p表示k+extend[k]-1,L=extend[i-k+1]*/ 21 if(i-k+l<tp-k+1) p[i]=l;/*第一种情况,直接记录就可以了*/ 22 else/*第二种和第三种归为一种*/ 23 { 24 int j=tp-i+1;/*定义一个变量j=p-i+1,表示当前从i开始和从1开始的公共前缀长度*/ 25 if(j<0) j=0;/*因为有可能有负数,所以直接变成0*/ 26 /*但是这两种合并为一种情况,为什么可以这么写呢? 27 因为p-i+1为正数的时候,j还是保留原来匹配的位置,是负数的话从0开始也是可以匹配1~i和j+1~i+j 28 只不过这个时候的j等于0而已,所以可以直接这样子做,比较方便*/ 29 while(sb[j+1]==sb[i+j] && i+j<=lenb) j++;/*判断一下i+j<=lenb*/ 30 p[i]=j;/*得出长度*/ 31 k=i;/*更新一下k*/ 32 } 33 } 34 ex[1]=lenb;/*ex匹配a串,一开始等于lenb,是不清楚的,只是暂且变成这个值*/ 35 for(int i=1;i<=lenb;i++) if(sa[i]!=sb[i]){ex[1]=i-1;break;} 36 /*位置不一样,就记录上一个答案,然后退出*/ 37 /*如果没有定义的话ex[1]=lenb的话,会在这里一直一直相同就跳不出来,而且还是等于lenb*/ 38 k=1; 39 for(int i=2;i<=lena;i++)/*因为1是通过匹配得到的,所以可以直接从2开始*/ 40 { 41 tp=k+ex[k]-1; l=p[i-k+1]; 42 /*tp也就是说我现在所到达的k最长的时候加上我这个和b串匹配的时候得到的长度 43 l表示在b串原串匹配到的i-k+1,这样就可以很方便的从b串的开头 44 定义:extend[i]表示以i为首和以开头为首的最长公共前缀长度,这个条件是保持在同一字符串里面的, 45 在这里就变成了:以a串的i为首和以b串的开头为首的最长公共前缀长度, 46 所以这样就可以求出a串匹配b串的ex数组*/ 47 if(i-k+l<tp-k+1) ex[i]=l; 48 else 49 { 50 int j=tp-i+1; 51 if(j<0); j=0; 52 while(sb[j+1]==sa[i+j] && i+j<=lena && j<=lenb) j++; 53 ex[i]=j; k=i; 54 } 55 } 56 } 57 int main() 58 { 59 scanf("%s%s",sa+1,sb+1); 60 lena=strlen(sa+1); lenb=strlen(sb+1); 61 EXKMP(); 62 for(int i=1;i<lena;i++) printf("%d ",ex[i]); 63 printf("%d\n",ex[lena]); 64 return 0; 65 }
(非注释版:这个的话理解了之后用这个作为自己回忆的方式,还是可以的)

1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 #include<cmath> 6 #include<iostream> 7 char sa[1000010],sb[1000010]; 8 int ex[1000010],p[1000010],lena,lenb; 9 inline void EXKMP() 10 { 11 p[1]=lenb; 12 int i=1,k; 13 while(sb[i]==sb[i+1] && i+1<=lenb) i++; 14 p[2]=i-1; k=2; 15 int tp,l; 16 for(int i=3;i<=lenb;i++) 17 { 18 tp=k+p[k]-1; l=p[i-k+1]; 19 if(i-k+l<tp-k+1) p[i]=l; 20 else 21 { 22 int j=tp-i+1; 23 if(j<0) j=0; 24 while(sb[j+1]==sb[i+j] && i+j<=lenb) j++; 25 p[i]=j; 26 k=i; 27 } 28 } 29 ex[1]=lenb; 30 for(int i=1;i<=lenb;i++) if(sa[i]!=sb[i]){ex[1]=i-1;break;} 31 k=1; 32 for(int i=2;i<=lena;i++) 33 { 34 tp=k+ex[k]-1; l=p[i-k+1]; 35 if(i-k+l<tp-k+1) ex[i]=l; 36 else 37 { 38 int j=tp-i+1; 39 if(j<0); j=0; 40 while(sb[j+1]==sa[i+j] && i+j<=lena && j<=lenb) j++; 41 ex[i]=j; k=i; 42 } 43 } 44 } 45 int main() 46 { 47 scanf("%s%s",sa+1,sb+1); 48 lena=strlen(sa+1); lenb=strlen(sb+1); 49 EXKMP(); 50 for(int i=1;i<lena;i++) printf("%d ",ex[i]); 51 printf("%d\n",ex[lena]); 52 return 0; 53 }