E 最小生成树 （骗子！！）

E 最小生成树

---

Description:

• 给出一个 \(n\) 个点的图，点编号从 \(1\) 到 \(n\) ， \(i\) 号点的点权为 \(a_i\) 。对于 \(\forall i,j\) \((1\le i\lt j\le n)\) \(i\) 号点 和 \(j\) 号点之间存在一条无向边，边权为 \(a_i+a_j\) 。请求出这个无向图的最小生成树的边权和。

  请回忆：

• 在 \(n\) 个点的图 \(G\) 中选择 \(n-1\) 条边，这 \(n-1\) 条边和 \(n\) 个点构成图 \(H\) ，图 \(H\) 满足其中任意两个点之间都存在一条路径使得这两个点联通，那么图 \(H\) 是图 \(G\) 的一个生成树。

• 在图 \(G\) 的所有生成树中，边权和最小的生成树称为图 \(G\) 的最小生成树。

Sample Input

3
5
2 2 1 1 1
6
11 12 11 13 12 13
1
3

Sample Output

10
116
0

Hint

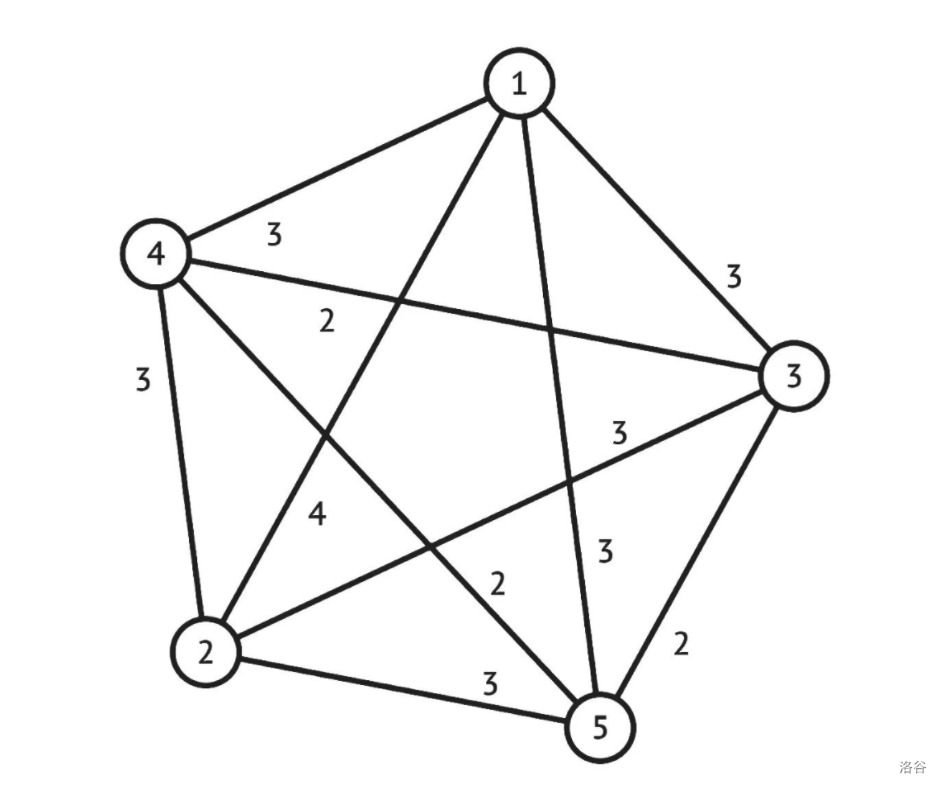
Constraints:

• \(1\le T \le 5\times 10^3\)
• \(1\le n \le 5\times 10^3\)
• \(1\le a_i\le 3\times 10^5\) 点权

---

Analysis:

• 贪心，把所有点连到点权最小的点上

---

Solution:

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;

void solve() {
	int n; cin >> n;
	vector<int> v;
	for(int i=0;i<n;i++) {
		int x; cin >> x;
		v.push_back(x);
	}
	sort(v.begin(),v.end());
	ll ans = 0; //不开long long见祖宗
	for(int i=1;i<n;i++) {
		ans += (v[0]+v[i]);
	}
	cout << ans << endl;
}

int main() {
	int T; cin >> T;
	while(T--) {
		solve();
	}
	return 0;
}