Codeforces 1857D：Strong Vertices 与图论无关的出度最大统计

1857D.Strong Vertices

---

Description:

• 给定两个长度均为 $n$ 的数组 $a$ 和 $b$ （编号$1$~$n$），如果 $a_u-a_v\ge b_u-b_v$ $(u\ne v)$，那么从 $u$ 到 $v$ 建立一条有向边。"Strong"定义为：一个点 $V$ 可以经过有向图中合法的通路到达其他所有的点。请求解出"Strong"点的数量和对应的编号（升序输出）。

---

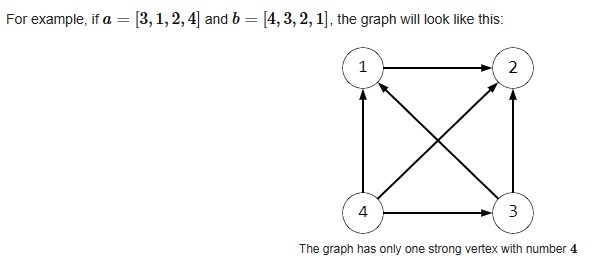
Constraints:

• $2\le n\le 2·{10}^5$
• $-{10}^9\le a_i,b_i\le {10}^9$

---

Analysis:

• 显然，数字这么大无法存图，那就从数字比较角度考虑。
• 对题目中的关系移项可得，$a_u-b_u\ge a_v-b_v$，出度最大的点是"Strong"，那肯定差值越大越可能，统计最大值出现的次数和对应下标即可
  （注意代码的写法细节以及 ${}^{\ast }max\mathrm{\_}element$函数 对于普通数组 $a[]$ 和$vector$ 的差别）

---

Solution:

void solve() {
	int n; cin >> n;
	vector<int> a(n+1),b(n+1);
	for(int i=1;i<=n;i++) cin >> a[i];
	for(int i=1;i<=n;i++) {
		cin >> b[i];
		a[i] -= b[i]; // a[i]-b[i]数组
	}
	// 如果是普通数组，maxx = *max_element(a+1,a+1+n);
	int maxx = *max_element(a.begin()+1,a.begin()+1+n);
	vector<int> ans;
	for(int i=1;i<=n;i++) {
		if(a[i] == maxx) ans.push_back(i);
	}
	cout << ans.size() << endl;
	for(auto t : ans) cout << t << " ";
	cout << "\n";
}