梯度方法求解最优投资组合问题 (二次规划问题)
**优化程序**
分析师的目标是帮助投资者“做最好的事”。他们的共同目标应该是制定一套投资策略,为投资者提供最大可能的效用。在某些情况下,这可以形式化为一个涉及目标函数最大化的问题(例如投资者的投资组合的效用),该问题受到一个或多个约束(例如投资者的财富水平所施加的约束)。在投资领域,解决这类问题的过程通常被称为最优化。有效地确定最优策略的过程通常被称为优化算法。毫不奇怪,使用这种程序的计算机通常被称为优化器。
接下来的小节,我们处理分析师经常会遇到的几类优化问题以及可用于解决这些问题的方法。
**标准的资产配置问题**
我们关注投资者的资产在几个资产类别之间的配置,以实现最大限度地提高投资者的资产组合效用,同时考虑投资者的风险容忍度和对资产持有的相关限制。许多分析师使用对资产风险、相关性以及预期收益的一期估计来解决这类问题,假设投资者的效用是所选投资组合的预期收益和收益标准差的函数。更准确地说,投资者的效用被表示为资产组合的均值和方差的线性函数:
其中
这里,\(rt\) 代表投资收益的方差替代期望的边际率。此外,衡量投资组合效用的 \(u\) 可以被解释为风险调整后的预期收益,因为它是通过从预期收益(\(ep\))中减去风险惩罚(\(vp/rt\))来计算的。
当然,一个投资组合的预期收益将取决于它的构成以及其组成部分的预期收益。投资组合由持股向量表示,以比例值表示。设 \(x\) 为这种比例(\(n*1\))的向量,\(e\) 为资产预期收益的(\(n*1\))向量。则投资组合 \(x\) 的预期收益为:
投资组合收益的方差将取决于其构成和各类资产类别之间的协方差。设 \(C\) 为这种协方差的(\(n*n\))矩阵。则投资组合 \(x\) 的收益方差为:
我们的目标是找到最佳投资组合--这里指的是具有最大可能效用的投资组合。决策变量是资产持有量--也就是向量\(x\)的元素。随着这些元素的变化,相关投资组合的效用也发生变化。我们希望改变它们,直到获得最大可能的效用。然而,在允许的组合上通常有一些限制。在标准问题中,\(x\) 值代表按比例持有的资产。在这种情况下,只有综合为 \(1\) 的 \(x\) 可以被考虑。因此,我们必须服从全投资约束:
通常会有进一步的资产持有约束。在许多情况下,卖空(short sales)是被禁止的,因此只允许 \(x\) 的非负值。上限也可能适用,标准问题中,我们有
只涉及下界的情况可以通过给上界赋正无穷值来处理,而只涉及上界的情况可以通过给下界赋负无穷值来处理。如果没有边界,两个过程都可以调用,这使得标准化问题的表述比人们最初假设的更为普遍。
我们将此称为“标准资产配置问题”,总结如下:
注意,这涉及到决策变量的二次函数的最大化,受制于一组线性约束,其中一些是不等式,具有这种特征的问题被称为一个二次规划(QP)问题。它可以用一般的二次规划算法来解决,也可以用专门设计来处理具有类似结构的问题的程序来解决。这里我们介绍一种可以简单直观地解决标准资产配置问题的算法。虽然它的应用范围有些有限,但它很容易编程,并阐明了适用于宏观投资分析中非常广泛的优化问题的关键经济学原理。
一个三资产的例子
为了说明优化过程的步骤,我们使用一个简单的例子,涉及三种资产---现金、债券和股票。它们的回报之间的标准差和相关性与1980年至1985年期间多元化指数共同基金的实际回报相似。预期收益与该时期的平均实际收益相似。所有的月值都是年变化的。值得注意的是,这段时期的平均回报率非常高。对未来预期的无偏估计很可能要低得多。
将所有与资产相关得关键信息包含在一个块中是很方便的。以下是我们示例的输入,格式化用于解决此类问题所提供的优化工作表:
| 最小值 | 初始化 | 最大值 | 期望回报率 | 标准差 | c:现金 | c:债券 | c:股票 | |
|---|---|---|---|---|---|---|---|---|
| 现金 | 0.00 | 1.00 | 1.00 | 2.80 | 1.00 | 1.00 | 0.4 | 0.15 |
| 债券 | 0.00 | 0.00 | 1.00 | 6.30 | 7.40 | 0.40 | 1.00 | 0.35 |
| 股票 | 0.00 | 0.00 | 1.00 | 10.80 | 15.40 | 0.15 | 0.35 | 1.00 |
第一列显示下界,第三列显示上界。第二列表示初始投资组合。在这种情形下,它的所有资产都以现金投资。第四列和第五列分别显示资产的预期收益和标准差,以每年的百分比回报表示(例如,股票预期回报 10.80% 一年)。最后几列提供了对资产类别之间相关性的估计。
在矩阵形式中,问题的输入是:
为了计算的目的,我们需要协方差矩阵\(C\):
这里
另一个输入是投资者的风险承受能力。这种情况下,我们假设它是\(50\)--一个代表对冒险的适度态度的值,即
**效用等值面**
尽管我们的例子中涉及三个决策变量(现金、债券和股票),但全投资约束将投资组合限制为总和为1的组合。因此,我们可以将这个问题描述为选择投资于债券和股票的比例,剩余的任何金额都用投资于现金。这样就有可能绘制出决策变量和价值衡量之间的关系图。生成的表面将具有山的一些属性。然而,这个"效用山"(等值面)中只有一部分是可行的。我们必须将搜索限制在债券和股票投资金额小于等于\(1\) 的坐标上。
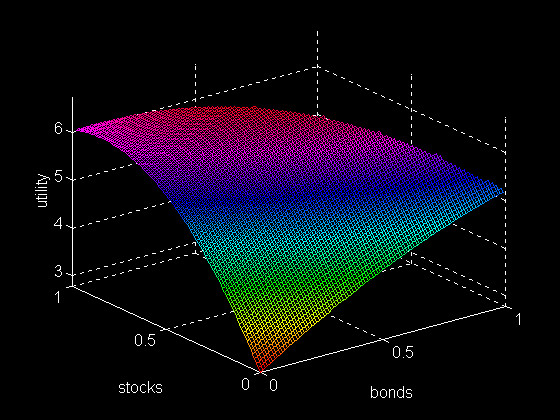
从某种意义上说,我们的工作就是爬到山上可行的最高点。我们将分阶段完成这项工作。我们从一个可行的投资组合开始。然后我们找到可行的方向,在这个可行的方向上我们可以以最大的速度向上移动。更具体地说,我们选择一步(投资组合持有量的变化)高度(效用)增加最大的方向--也就是梯度的方向。选择了一个方向,我们就会一直往上爬,直到到达一个高峰或一个我们无法跨越的边界。然后我们再次确定最陡峭爬坡的可行方向,重复这个过程。当没有可行的上升方向时,我们就停止。
**资产边际效用**
考虑持有一种资产的微小变化对投资组合效用的影响。回想一下:
设\(mu(i)\)为资产\(i\) 的边际效用--\(u\)对\(x_{i}\) 的导数
有了这,我们可以直接计算\(mu\)
其中\(x\) 是当前的投资组合。在这个例子中,我们从当前投资组合\(x_{0}=(1 \ 0 \ 0)^{T}\) 开始,得到的边际效用是:
因此,只要资产\(3\) 的变动较小,效用将以每单位投资金额变动的\(10.7076%\) 的速率变化。同理,资产2的变化率为\(6.1816%\),资产3 的变化率为\(2.7600%\).
**最优可行交换**
边际效用提供了关于投资组合的重要信息,这些信息可以用来改善投资组合,改变投资组合的构成,从而增加投资者的效用。
在这种情况下,所有的边际效用都是正的,这表明任何资产的增加都会增加效用。如果我们能够增加对这三种资产的投资比例,或者更好的是只增加对这三种资产中最好的资产的投资比例,那就太好了。但这是不可行的。唯一可以考虑的变化是那些满足比例和等于 1 的约束的变化。因为这已经是当前投资组合的情况,我们必须限制我们的选择,使我们增加一项或多项资产的金额之和等于我们减少一项或多项其他资产的金额之和。
在这个例子中,最优吸引力的增加资产是第三种(股票)。令人高兴的是,它可以增加,因为当前金额为0,低于上限1。最没有吸引力的增加资产是第一项(现金)。但是它也是最吸引减持的资产。这暗示了一种双资产互换,即资产 3 增加,资产 1 减少。这样的互换将以 \(10.7076-2.7600\) 或 \(7.9476%\) 的单位交换量的速率增加效用,只用后者的变化较小。幸运的是,这种特殊的交换是可行的,因为(1):要增加的资产目前低于其上限;(2):要减少的资产的当前值为 1.00,远高于其下限值 0.00。
我们得出的结论是:如果要进行一次小型的两种资产互换,最好的可能性是减少现金的数量,同时增加投资于股票的数量。如果实际持有当前的投资组合,则需要出售现金,所得款项用于购买股票。在更有可能的情况下,正在进行以确定持有的最佳投资组合,“买入”和“卖出”将是假设的。然而,为简单起见,我们使用术语“卖出”,“买入” 和 “交换” 来描述这两种情况。
在这种类型的问题中,只有当要减少的资产高于其下界 而要增加的资产低于其上界时,互换才是可行的。此外,如果当前的投资组合满足约束,即持有资产的综合等于 1,那么任何由这种互换产生的投资组合也将是可行的,只要互换的幅度不是太大。由于在标准问题中不存在额外的约束,因此,这些条件既是交换可行的必要条件,也是充分条件。这些观察结果引出了寻找最优可行双安全交换的规则:
显然,如果\(mu(ibuy)-mu(isell)\) 为正,则投资组合的效用可以增加。而且,其他再小的变化也不能使效用增加这么多,因为是最大的减去最小的。因此,最优的两种证券互换是标准问题中的最优互换。
**最优的可行互换金额**
最优可行交换将以最大可能的单位交换率增加效用。但增加的速度会随着交换规模的增加而变化。在某一时刻,效用将达到顶峰,然后下降。此外,互换的可行金额将受到购买资产的上界和出售资产的下界的限制。所有这些因素都需要考虑,以便为任何期望的交换找到最优可行规模。
为了通用性,我们用资产持有变化的向量 \(s\) 来表示交换,其中元素的总和为零。在我们的例子中,最优可行交换是:
现在,设 \(a\) 代表交换的金额,因此,净效果是改变投资组合的金额等于\(s*a\)。
例如,如果 \(a=0.1\),
设 \(cx\) 表示这组变化:
那么,如果对投资组合 \(x\) 进行这样的改变,结果将是一个新的投资组合 \(xx\),给出如下:
或者
现在,我们考虑投资组合 \(x\) 和 \(xx\) 的效用:
我们感兴趣的是效用的变化 \(cu=u(xx)-u(x)\)。展开第二个公式,减去第一个公式,得到
用 \(s*a\) 代替 \(cx\),化简得到
重新排列,将 \(cu\) 表示为交换量 \(a\) 的函数,我们得到
其中
在我们的例子中,
下面将 \(cu\) 绘制为 \(a\) 的函数
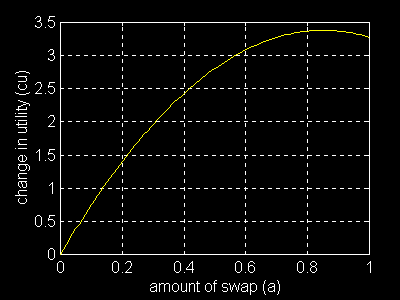
注意,效用的变化是以递减的速率增加的。这并不奇怪,因为函数是二次的,有一个负的二次项。这是投资组合构成中,所有变化的一个特征。鉴于协方差矩阵的性质,对于向量 \(s\) 表示的任何一组变化, \(s^{T}Cs\) 都为正。只要投资者的风险承受能力为正,\(k1\) 也将为正。因此,我们得出结论:
投资组合修正受制于规模收益递减。修正幅度越大,投资组合效用进一步增长的速度就越小--也就是说,效用将以递减的速度增长。
注意,这个表达式中的第一项 \(k0\) 等于交换的净边际效用。这并不奇怪,因为边际效用衡量的是持有量无限小的变化对效用的影响。
在这种情况下,效用的最大可能变化是通过交换大量的投资组合来获得的。实际的金额可以直接计算出来。我们求 \(a\)的值,此时 \(cu\) 最大。由于 \(cu\) 在原点处的斜率必须为正,切斜率必须随 \(a\) 减小,因此,我们只需要将倒数设为零,
在这种情况下,
因此,最优交换金额为0.8508。
当然,这个计算并没有考虑到持仓的上下界。为了保持可行性,交换的最优可行数量为:
在我们的例子中,
所以,交换的最优量将在原来投资组合的效用上增加3.3808个单位。
**标准问题的算法(An algorithm for the Standard Problem)**
现在我们有了解决标准问题所需的所有成分。从任何可行的投资组合开始,我们可以找到最优可行互换和该互换的最优金额。 在进行适当数量的交换后,我们得到了一个新的(改进的)可行投资组合。但这也可以改进,使用相同的技术。通过重复这个过程,直到没有进一步改进的可能,我们在不违反所描述约束的情况下,达到了效用最大化的目标。
该算法的中心部分使用了一个循环,该循环一直持续到终止条件得到满足。这可以在伪-Matlab中写为:
% Loop
while 1==1
[ do computations ]
if [ finished ]
return
end;
end;
当然,首先需要一个可行的投资组合。假设 \(x_{0}\) 满足这个要求,我们在循环之前加上
这也将 \(n\) 设置为以后使用的资产数量。
在循环内部,首先进行的计算是计算边际效用,找到最适合购买和最适合出售的资产。为了说明起见,我们以一种有些低效的方式来做这件事,如下所示:
% compute marginal utilities
mu = e - (1/rt)*2*C*x;
% find best assets to buy and sell
ibuy = 0;
mubuy = -1E200;
isell = 0;
musell = 1E200;
for i = 1:n
if x(i) < ub(i) % possible buy
if mu(i) > mubuy
mubuy = mu(i);
ibuy = i;
end;
end;
if x(i) > lb(i) % possible sell
if mu(i) < musell
musell = mu(i);
isell = i;
end;
end;
end;
这个时候就该检查一下,看看这个程序是否应该终止。如果与最优可行交换的边际效用净变化率为零或负,则不可能再有改进。考虑到计算机的误差性质,当这个量小于某个最小阈值时,最好终止。例如
% terminate if change in mu is less than threshold value
if (mubuy - musell) <= 0.0001
return
end
在优化工作表中,该常数称为边际效用截止值。如果速度比精度更重要,则应该将其设置为较大的值(比如 0.001)。如果精度比速度更重要,它应该设置为一个相对较小的值(比如 0.00001)。
请注意,终止程序也适用于没有剩余资产可购买和/或出售的情况,因为我们已将 \(mu(sell)\) 和 \(mu(buy)\) 的值非常大和非常小。有点迂回,但很有效。
如果没有终止,那么就该交换了。首先,我们建立描述最优交换的向量:
% set up swap vector
s = zeros(n,1);
s(ibuy) = 1;
s(isell) = -1;
然后我们在不考虑资产边界影响的情况下,计算出最优的交换量:
% compute optimal amount of swap without regard to asset bounds
k0 = s'*(e - (1/rt)*2*C*x);
k1 = (s'*C*s)/rt;
a = k0/(2*k1);
这可能可行,也可能不可行。必要时,减少要交换的金额,避免违反要购买的资产的上界或要出售的资产的下界:
% reduce amount if required to keep ibuy from exceeding its upper bound
if a > (ub(ibuy) - x(ibuy))
a = ub(ibuy) - x(ibuy);
end;
% reduce amount if required to keep isell from falling below its lower bound
if a > (x(isell) - lb(isell))
a = x(isell) - lb(isell);
end;
为了避免无线循环的可能性,明智的做法是检查是否为零(交换金额),并在遇到这种情况时终止:
% terminate if amount is zero
if a == 0
return;
end
最后,是时候修改投资组合了,尽可能地完善它,并且能够中心重复这个过程:
% change mix
x = x + ( s*a) ;
这是将整个算法设置为一个MATLAB函数,将 \(rt, e, C, lb, ub, x0\) 做为输入,并返回最优投资组合 \(x\) 做为输出。
% main
function x = gmqp(rt,e,C,lb,ub,x0);
% determines solution to a standard optimization problem
% usage:
% x = gmqp(rt,e,C,lb,ub,x0);
% rt = Investor risk tolerance
% e = {n*1} vector of asset expected returns
% C = {n*n} return covariance matrix
% lb = {n*1} vector of asset lower bounds
% ub = {n*1} vector of asset upper bounds
% x0 = {n*1} vector of initial feasible asset mix
% set initial mix and number of assets
x = x0;
n = length(x);
while 1==1;
% compute marginal utilities
mu = e - (1/rt)*2*C*x;
% find best assets to buy and sell
ibuy = 0;
mubuy = -1E200;
isell = 0;
musell = 1E200;
for i = 1:n
if x(i) < ub(i) % possible buy
if mu(i) > mubuy
mubuy = mu(i);
ibuy = i;
end;
end;
if x(i) > lb(i) % possible sell
if mu(i) < musell
musell = mu(i);
isell = i;
end;
end;
end;
% terminate if change in mu is less than threshold value
if (mubuy - musell) <= 0.0001
return
end
% set up swap vector
s = zeros(n,1);
s(ibuy) = 1;
s(isell) = -1;
% compute optimal amount of swap without regard to asset bounds
k0 = s'*(e - (1/rt)*2*C*x);
k1 = (s'*C*s)/rt;
a = k0 / (2*k1);
% reduce amount if required to keep ibuy from exceeding its upper bound
if a > (ub(ibuy) - x(ibuy))
a = ub(ibuy) - x(ibuy);
end;
% reduce amount if required to keep isell from falling below its lower bound
if a > (x(isell) - lb(isell))
a = x(isell) - lb(isell);
end;
% terminate if amount is zero
if a == 0
return;
end
% change mix
x = x + ( s*a) ;
end;
用此函数在MATLAB路径下的目录下命名为 gmqp.m,您可以在命令行或程序中简单地给出以下命令来获得标准问题的解:
x=gmqp(rt,e,C,lb,ub,x0)
对于我们的问题
因此,最优的投资组合不含现金,大约 40% 投资于债券, 60% 投资于股票。
**函数GQP**
虽然函数 gmqp 足以解决大多数标准问题,但他不能处理 \(rt=0\) 的情况,因为 \(rt=0\) 会导致试图将投资组合方差除以 \(0\)。然而,出现了经济上有意义的问题,其目标是最小化方差,对风险零容忍的投资者也是如此。这种情况可以通过改变衡量效用的单位来解决。而不是:
我们可以用
更常用的版本(u)将投资组合方差除以rt,即方差对预期收益的边际替代率,将 vp 转换为预期收益的等价物。然后将后者从投资组合预期收益中减去,得到 \(u\),已预期收益的形式衡量投资组合效用。
第二个度量(uv)将投资组合预期收益乘以rt,即方差对预期收益的边际替代率,将 ep 转换为方差当量。然后减去投资组合方差,以方差等效的方式获得投资组合效用的度量。当 \(rt=0\)时,最大化 \(uv\) 相当于最小化最小化投资组合方差,如期望的那样。当 \(rt\) 大于 0 时,最大化 \(uv\) 将得到与最大化 \(u\) 相同的组合 \(x\)。
将此修改合并到MATLAB函数 ggp.m 中,可以代替 gmqp使用。函数 ggp 有许多额外的功能。它使用更有效的向量方法来找到最优交换和适当的交换量,因此比 gmqp 更块。它还计算投资组合的预期收益和方差,并在需要时将其作为附加输出返回。
用 gqp 函数在MATLAB 路径下的目录下命名 gqp.m, 您可以通过在命令行或程序中简单地给出以下命令来获得标准问题的解:
[x,ep,vp]=gqp(rt,e,C,lb,ub,x0)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号