关于APIT定位算法的讨论

关于APIT定位算法的讨论

【摘要】   无线传感器网络节点定位机制的研究中，基于距离无关的定位技术得到快速发展，其中基于重叠区域的APIT定位技术在实际环境中的定位精度高，被广泛研究和应用。

【关键词】 无线传感器网络；定位算法；APIT；

 

 

【正文】

在传感网络中的许多应用中，用户一般都会关心一个重要问题，即特定时间发生的具体位置或区域。例如，目标跟踪，入侵检测，环境监控等，若不知道传感器自身的位置，感知的数据是没有意义的。因此，传感器网络及诶单必须知道自身所在的位置，才能够有效地说明被检测物体的位置，从而实现对外部目标的定位，跟踪等。

 

作为一种全新的技术，无线传感器网络具有许多挑战性的研究课题，定位技术就是其中之一，定位也是大多数应用的基础和前提。

 

目前定位技术主要有两个类型：给予测距的定位技术和基于非测距定位技术。

 

基于测距的定位技术涉及几何中的图形问题，已知节点的位置，求另几个节点的位置，比较常用的方法是三边定位和角度定位，这类算法比较简单，实现容易，但是他们受到电磁干扰，多径干扰等因素的影响。

 

基于非测距定位技术，无需利用这些基础设施来测量位置节点同信标节点之间的距离和角度这些信息，只需要根据未知节点是否连通，或者未知节点之间的跳数来度量。极大地降低了对环境的依赖性。在这篇文章中，我选取了其中具有代表性的APIT定位算法来进行讨论。

 

 

APIT定位算法

1.   初始

APIT(Approximate PIT) 定位算法的理论基础是最佳三角形内点测试法PIT(Perfect Point-In-Triangulation Test)。

 

 

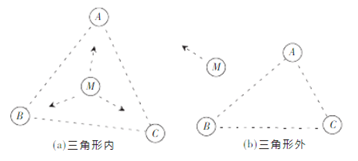
PIT理论为判断某一点M是否在三角形ABC内，假如存在一个方向，沿着这个方向M点会同时远离或者接近三角形ABC的三个顶点，那么M位于三角形ABC，否则位于三角形ABC外。

 

2.   优化

但是无线传感网络中大部分节点是静止的，不可能随意的像上述一样通过移动节点测试是否在三角形中，为了在静态网络中执行PIT测试，定义了APIT测试。

 

 

 

APIT定位算法最关键的步骤是测试未知节点是否在三个信标节点所组成的三角形内部。APIT算法是基于PIT测试原理的改进，可以领用WSN较高的节点密度和无线信息的传播特性来判断是否远离和靠近信标节点。通常在给定方向上，一个节点距离信标节点越远，接收信号的强度越弱。通过与邻居节点信息交换，来效仿PIT测试的节点移动。例如：

 

 

 

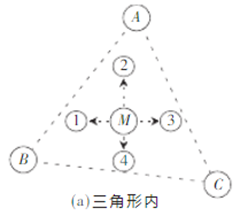
图a中，位置未知节点M通过与邻居节点1交换信息，得知自身如果运动到节点1，将远离信标B和C，但是会接近信标节点A，同样通过与邻居节点2，3，4交换信息，最终确定自身位于三角形ABC中。

 

 

 

 

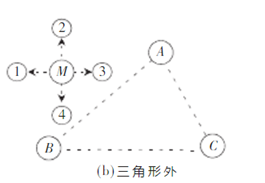
图b中，当节点通过邻居节点2得知，将会同时远离信标节点ABC，故判断自身不在三角形ABC中。

 

 

3.   确认

在APIT算法中，一个未知节点任选三个相邻信标节点，若通过测试发现自己位于他们所组成的三角形中，则认为该三角形的质心即为未知节点的位置，然后进一步选用不同信标节点的组合重复测试，直到穷尽所有组合或者达到所需定位精度为止；最后计算包含目标节点所有三角形的交集质心，并以此为未知节点的最终位置。

 

 

 

源码分析

本次实验均用matlab程序编写：

 

1.   初始化布局

C_random(area,node n,anchors_n,GPS_error)：

参数：区域，节点数，信标节点，GPS误差。

 

function C_random(area,nodes_n,anchors_n,GPS_error)

% deploy the nodes over a C-shaped region

% area: the sensing region [200 40 40 160]

%   the side is 200m-long, x=40,y=40,y=160: the edge of C-shaped region

% nodes_n: the number of nodes

% anchors_n: the number of anchors

%   if anchors_n<1, it means the ratio;

%   if anchors_n>1, it means the number

% GPS_error:the max location error of anchor raised by GPS, default is 0;

%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

% C_random([200 40 40 160],150,0.1)

C_random([1000,100,1000,0],240,0.2);

 

 

 

 

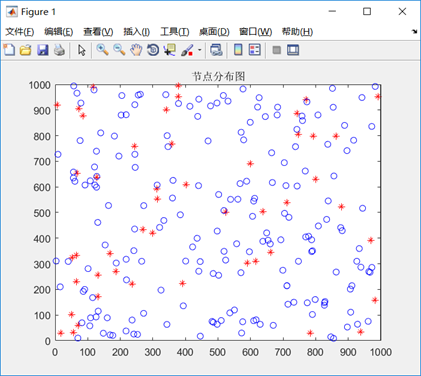
240个节点,其中48个锚节点

红色*表示锚节点，蓝色O表示未知节点

 

 

2.   计算未知节点坐标

if neighboring_anchor_n>=3

            gridmap=zeros(row_n,col_n);

            grid_covered_flag=zeros(row_n,col_n);

            for a=1:neighboring_anchor_n-2

                for b=a+1:neighboring_anchor_n-1

                    for c=b+1:neighboring_anchor_n

                        % 判断未知节点i是否在三角形abc内部

                        % Approximate P.I.T Test: "If no neighbor of M is further from/close to all three anchors A, B and C simultaneously,

                        % M assumes that it is inside triangle abc. Otherwise,M assumes it resides outside the triangle."

                        neighboring_node_index=setdiff(find(neighbor_matrix(i,:)==1),neighboring_anchor_index([a b c]));

                        neighboring_node_rss_of_abc=neighbor_rss(neighboring_node_index,neighboring_anchor_index([a b c]));

                        in_out_judge=neighboring_node_rss_of_abc>repmat(neighbor_rss(i,neighboring_anchor_index([a b c])),length(neighboring_node_index),1);

                        if any(sum(transpose(in_out_judge))==0|sum(transpose(in_out_judge))==3)%outside                       

                            Grid_in_triangle_abc=inpolygon(centroid_x,centroid_y,all_nodes.estimated(neighboring_anchor_index([a b c]),1),all_nodes.estimated(neighboring_anchor_index([a b c]),2));%被三角形abc覆盖到网络

                            gridmap=gridmap-Grid_in_triangle_abc;                             

                        else%inside

                            Grid_in_triangle_abc=inpolygon(centroid_x,centroid_y,all_nodes.estimated(neighboring_anchor_index([a b c]),1),all_nodes.estimated(neighboring_anchor_index([a b c]),2));%被三角形abc覆盖到网络

                            gridmap=gridmap+Grid_in_triangle_abc;                           

                        end

                        grid_covered_flag=grid_covered_flag|Grid_in_triangle_abc;

                    end

                end

            end          

 

 

 

3.   定位误差

 

 

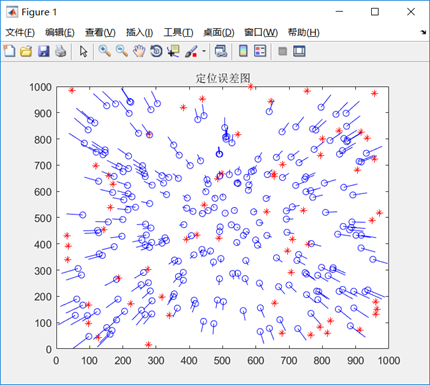
红色*表示锚节点

蓝色O表示未知节点的估计位置

黑色O表示不能被定位的未知节点

蓝色-表示未知节点的定位误差(连接未知节点的估计位置和真实位置)

一共300个节点:60个锚节点,240个未知节点,0个不能被定位的未知节点

定位误差为0.17819

 

 

算法总结

APIT定位的具体步骤如下所示：

l  收集信息：未知节点收集邻近信标节点的信息。

l  APIT测试：测试未知节点是否在不同的信标节点组合的三角形内部。

l  计算重叠区域：统计包含未知节点的三角形，计算所有三角形的重叠区域。

l  计算未知节点位置：计算重叠区域的质心位置，作为位置节点的位置。

 

 

展望与发展

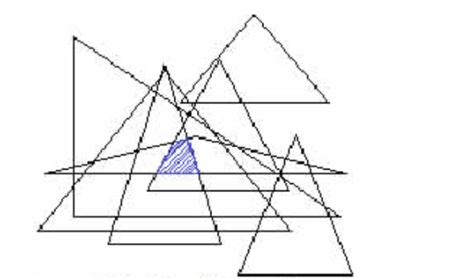
在整个无线传感器网络的边缘地区，传感器的数量相对比较少，信标节点较少，这样组成的三角形的数量也会降低。在进行APIT测试定位时，会出现由于重叠区域过大而造成实际位置与定位位置偏差过大的现象。如图所示，是运用APIT定位误差较大的一种情况。

 

为了提高无线传感器网络的定位精度，APIT算法需要继续改进，现已有很多专家学者进行过讨论，这里只举例其中两种：

l  将三角形进行中垂线分割成4个或者6个小区间，通过对各个目标节点收到目标节点信号的强度进行比较，判断目标节点位于哪一个小区间中。

l  通过任意一个信标节点对另外两个信标节点所在直线作垂线得到垂直交点，通过比较这个信标点到交点的距离和他与位置节点的距离的关系，初步判断未知节点未知，同时，通过加权质心定位算法得到未知节点的精确估计。

 

参考文献

【1】      刘伟荣，何云. 物联网与无线传感器网络

【2】      唐明虎，张长宏. 无线传感器网络APIT定位算法

【3】      张冬冬，常用定位技术的实现

【4】      海子，www.cnblogs.com/dolphin0520

【5】      戴天虹，李昊，基于改进APIT算法的无线传感器网络节点定位

【6】      杨凌云，冯友宏，垂直交点APIT定位改进算法