确定性时间序列
移动平均法
栗子:P168
某个企业1~11月的销售输入时间序列,用一次简单移动平均法预测第12个月的销售收入。
clc,clear y = [533.8 574.6 606.9 649.8 705.1 772.0 816.4 892.7 963.9 1015.1 1102.7]; m = length(y); n = [4,5]; for i = 1 : length(n) for j = 1:m-n(i)+1 yhat{i}(j) = sum(y(j:j+n(i)-1))/n(i); end y12(i) = yhat{i}(end); s(i) = sqrt(mean(y(n(i)+1:end)-yhat{i}(1:end-1)).^2); end y12,s
公式很简单:
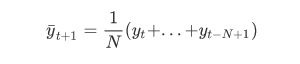
标准误差为:
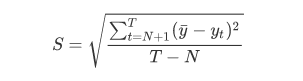
指数平滑法
- 一次
栗子P171
某市1976-1987年某种电器销售额如表所示。预测1988年改电器销售额。
采用指数平均法
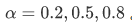
clc,clear; yt = load('dianqi.txt'); n = length(yt); alpha = [0.2 0.5 0.8]; m = length(alpha); yhat(1,[1:m]) = (yt(1)+yt(2))/2; for i = 2:n yhat(i,:) = alpha*yt(i-1)+(1-alpha).*yhat(i-1,:); end err = sqrt(mean(repmat(yt,1,m)-yhat).^2); xlswrite('dianqi.xls',yhat); yhat1988 = alpha*yt(n)+(1-alpha).*yhat(n,:);
公式也很简单:
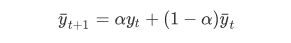
误差公式:
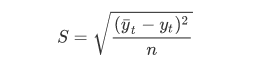
- 二次
clc,clear; yt = load('fadian.txt'); n = length(yt);alpha = 0.3;st1(1) = yt(1);st2(1) = yt(1); % 一次,二次 for i = 2:n st1(i) = alpha*yt(i)+(1-alpha)*st1(i-1); st2(i) = alpha*st1(i)+(1-alpha)*st2(i-1); end xlswrite('fadian.xls',[st1',st2']); at = 2*st1 - st2; bt = alpha/(1-alpha)*(st1-st2); % 综合一次,二次 yhat = at + bt; xlswrite('fadian.xls',yhat','Sheet1','C2'); str = ['C',int2str(n+2)]; xlswrite('fadian.xls',at(n)+2*bt(n),'Sheet1',str);
公式很简单:
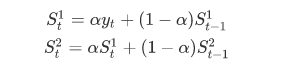
当时间序列 {yt} 在某时刻开始具有直线趋势时,可用直线趋势模型进行预测:
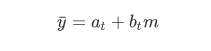
其中:
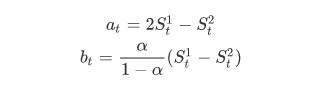
- 三次
当时间序列的变动表现为二次曲线趋势时,使用三次指数平滑法。
三次平滑模型P174,嘿嘿!!!
差分指数平滑法
差分指数平滑要解决的问题和前面的指数平滑是一样的,只是在预测时的公式不一样而已。
具有季节性特点的时间序列的预测
一,先预测年份(下一年)的年加权平均,
二,再预测年份的季度平均值
三,最后预测第 j 个季度的预测值。
clc,clear; format long g a = load('jijie.txt'); [m,n] = size(a); a_mean = mean(mean(a)); aj_mean = mean(a); % 计算季节系数 bj = aj_mean/a_mean; % 预测年份(下一年)的年加权平均 w = 1:m; yhat = w*sum(a,2)/sum(w); % 计算预测年份的季节平均 yjmean = yhat/n; % 预测年份的季节预测值 yjhat = yjmean*bj; format
公式如下:
收集m年的每年各个季度(月份) n 个季度的样本数据 aij
计算每年所有季度或者所有月份的算术平均值:
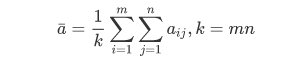
计算同季度(月份)的算术平均值:
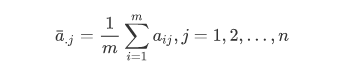
计算季度(月份)系数:
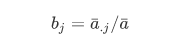
三部预测:
年份预测:
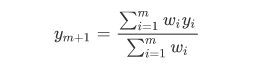
季度平均:
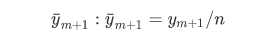
季度预测:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号