TSP 遗传算法

GA——遗传算法

同模拟退火算法一样，都是现代优化算法之一。模拟退火是在一定接受程度的情况下仍然接受一个比较差的解。

遗传算法，是真真正正的和大自然的遗传进化有着非常紧密的联系的，当然遗传进化的只是在生物学中已经讲过了，8个字，物竞天择，适者生存。

 

• 简介

《物种起源》，有兴趣可以看看达尔文的著作。

物竞天择，适者生存，这两句话，也可以说是对遗传算法过程的伪代码描述了，物竞天择，就是我们的目标函数，只有越满足我们的目标函数的个体才会留下来，适者生存，就是我们在算法的过程中要淘汰一些个体。

• 基因编码方式

生物学里面告诉我们，遗传，变异都是以种群为研究对象的，怎么表示一个解呢？用他的基因表示，嘿嘿，组成这个解的步骤表示，第一步干什么，第二步干什么，怎么在程序中编码呢？

常用两种编码方式：二进制编码，浮点数编码。

二进制编码：一定精度的二进制只能表示一定精度的浮点数。栗子，要求精确到6位小数，而区间是 [-1,2]，至少要把区间划分为3*10^6等分。编码也就需要22位。这里就涉及到一个二进制串转换到一个区间为 [-1,2] 的实数，两者相互转换。比如得到的十进制数为 x，那么对应的 [-1,2] 区间的浮点数就是

 

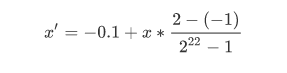
浮点数编码：为改善遗传算法的复杂度，提出来浮点数编码

• 适应评分及选择函数

适应评分函数就是用来衡量哪个个体应该被淘汰。但是也不能说，取值差点的个体一定就被淘汰了，这里会有一个概率存在，怎么建立一种概率关系呢？常用的方法是轮盘法。假设种群数为 n，某个个体 i 的适应度为 fi，那么个体 i 被选择的概率是：

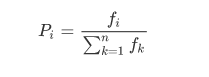
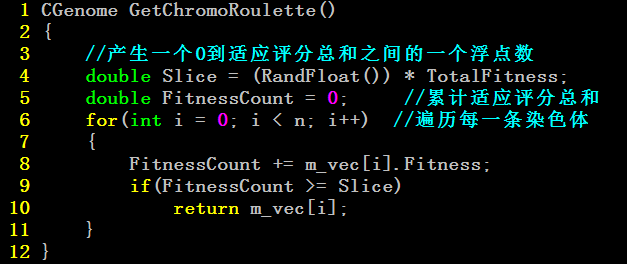
So，遗传算法中的自然选择过程：

适应评分函数——求出各个体的适应评分值

轮盘选择——个体被选择的概率

• 基因重组与基因突变

在生物学中，基因重组有两种情况。

 

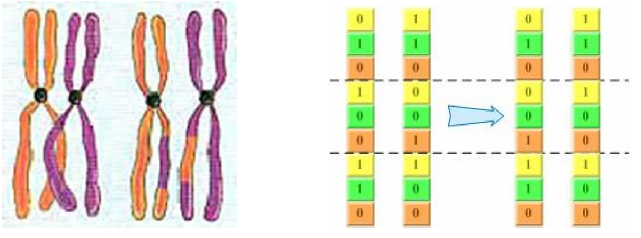
基因重组，就是两个个体基因发生交换。

基因突变是一种小概率事件。

使得一个基因变成他的等位基因，引起一定的表现型变化。

 

• TSP问题求解

TSP问题，之前已经用费用流，和模拟退火做过了，现在用遗传来讨论。

程序过程和自然界中的遗传与进化是一样的。

1. 生成50个个体，形成种群，并基因编码。

2. 基因重组，突变，和父代，一起进行天择。

3. 重复100次进化。得到较优的解。

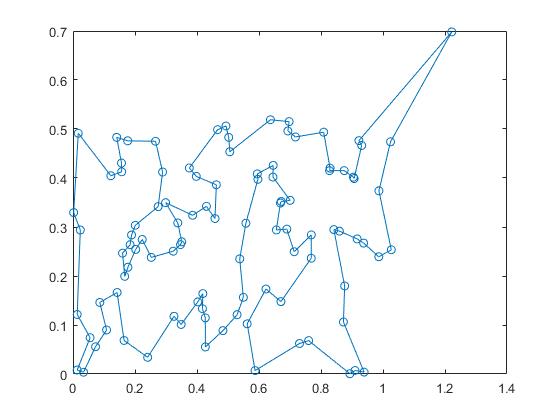
clc,clear;
sj0 = load('sj.txt');
x = sj0(:,1:2:8); x = x(:);
y = sj0(:,2:2:8); y = y(:);
sj = [x,y];d1 = [70,40];
sj = [d1;sj;d1]; sj = sj*pi/180;
​
d = zeros(102);
​
for i  = 1:101
    for j = i+1:102
        d(i,j) = 6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
    end
end
​
d = d + d';
% w 为种群数,g为进化的代数
w = 50;
g = 100;
rand('state',sum(clock));
​
% 改良圈算法选取初始种群
for k=1:w  %通过改良圈算法选取初始种群
    c=randperm(100); %产生1，...，100的一个全排列  
    c1=[1,c+1,102]; %生成初始解
    for t=1:102 %该层循环是修改圈
        flag=0; %修改圈退出标志
        for m=1:100
            for n=m+2:101
                if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))<d(c1(m),c1(m+1))+d(c1(n),c1(n+1))
                    c1(m+1:n)=c1(n:-1:m+1);  flag=1; %修改圈
                end
            end
        end
        if flag==0
            J(k,c1)=1:102; break %记录下较好的解并退出当前层循环
        end
   end
end
​
% 染色体编码
J(:,1) = 0;
J = J/102;
​
% 100次进化
for k = 1:g
    A = J;
    c = randperm(w);
    for i = 1:2:w                       % 基因重组
        F = 2 + floor(100*rand(1));     % 产生交叉操作的染色体对
        tmp = A(c(i),[F:102]);
        A(c(i),[F:102]) = A(c(i+1),[F:102]);
        A(c(i+1),F:102) = tmp;
    end
​
    % 变异
    by = [];
    while ~isempty(by)      % 变异的个体数也是随机的
        by =find(rand(1,w)<0.1);
    end
    
    B = A(by,:);        % 变异染色体
    for j = 1:length(by)
        bw = sort(2+floor(100*rand(1,3)));      % 产生变异操作的3个地址
        B(j,:) = B(j,[1:bw(1),bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]);
        
    end
    
    G=[J;A;B];       % 父代和子代
    % 基因翻译为解空间,把染色体翻译成1,...,102的序列ind1
    [SG,ind1] = sort(G,2);
    num = size(G,1);        % 父子种群的总个体数
    long = zeros(1,num);
    
    % 每一个体的优劣
    for j = 1:num
        for i = 1:101
            long(j) = long(j)+d(ind1(j,i),ind1(j,i+1));
        end
    end
    
    [slong,ind2] = sort(long);
    J = G(ind2(1:w),:);
end
​
path = ind1(ind2(1),:);
flong = slong(1);
xx = sj(path,1);
yy = sj(path,2);
plot(xx,yy,'-o');

 

参考：

ACdreamer

司守奎