因子分析——建立载荷矩阵
到这里已经学了好多的多元分析方法了,有聚类分析法,有主成分分析法,尤其是主成分分析法,为什么还要讨论因子分析法呢?很多地方都有对主成分分析法和因子分析法的区别比较,这里就不多说了,只记录一下最重要的地方。
主成分分析法:是对原始变量的线性组合,且相互垂直。
因子分析法:研究众多变量之间的内部依赖关系,潜在的假想变量+随机变量的线性组合。

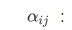
因子载荷,反映了第 i 个变量与第 j 个公共因子的相关系数,反映了第 i 个变量与第 j 个公共因子的相关重要性。绝对值越大,相关的密切程度越高。
因子载荷矩阵的估计方法:
-
主成分分析法
-
主因子法
-
极大似然估计
这里就只用其中一种方法解决吧,好像大部分都用的是主成分分析法。
举个栗子吧,P243,公司股票有5个因素影响,探讨一下这5个因素的内在联系。
clc,clear; r=[1.000 0.577 0.509 0.387 0.462 0.577 1.000 0.599 0.389 0.322 0.509 0.599 1.000 0.436 0.426 0.387 0.389 0.436 1.000 0.523 0.462 0.322 0.426 0.523 1.000]; % 利用关系矩阵进行主成分分解 [vec1,val,rate] = pcacov(r); f1 = repmat(sign(sum(vec1)),size(vec1,1),1); vec2 = vec1.*f1; % 使得每个特征向量分量和为正 % 因子分析公式 f2 = repmat(sqrt(val)',size(vec2,1),1); % 全部的因子的载荷矩阵 a = vec2.*f2; % 提取第一个因子的载荷矩阵 a1 = a(:,1); % 计算第一个因子的特殊方差 tcha1 = diag(r-a1*a1'); % 提取两个因子的载荷矩阵 a2 = a(:,[1,2]); % 计算两个因子的特殊方差 tcha2 = diag(r-a2*a2'); % 求两个因子时的残差矩阵 ccha2 = r - a2*a2' - diag(tcha2); % 求累积贡献率 con = cumsum(rate);
之前说主成分分析已经是很复杂的多元分析方式了,看来这句话说早咯!!!
首先用主成分分析对相关系数矩阵操作,求出特征向量,特征值,和主成分贡献率。
然后变形使得每个特征向量的分量和为正。
利用特征值和载荷矩阵公式求出载荷矩阵:
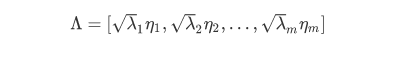
载荷矩阵求出来以后:
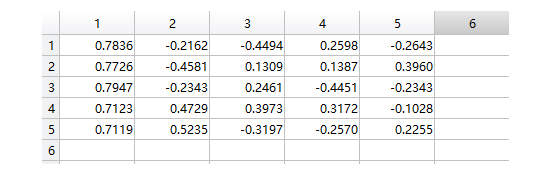
然后依然进行需要,选择因子的个数。
比如选择一个 F1 公共因子。
那么就可以表示5个变量(5种股票)的内在关系:

并对此进行分析:
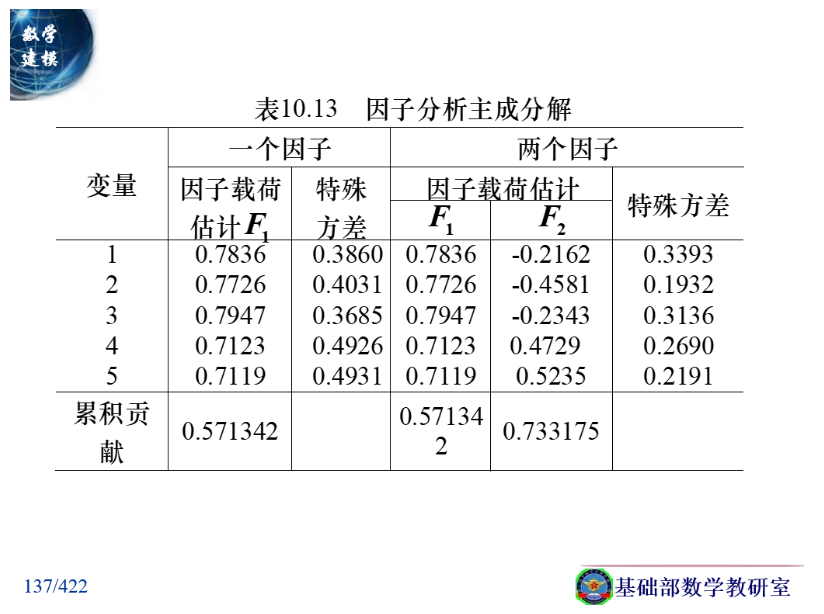
特殊方差是什么呢? 其实可以理解为从原来的变量到公共因子空间的转换效果的一个评价。
公式:
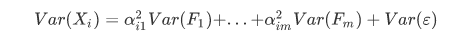
即:
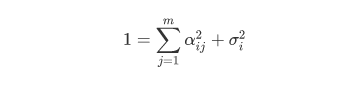


 浙公网安备 33010602011771号
浙公网安备 33010602011771号