聚类分析

聚类分析

Q型聚类

评价两两之间的距离有很多，绝对值距离，欧式距离，切比雪夫距离，马氏距离。

举个栗子P219

clc,clear;
a = [1 0
    1 1
    3 2
    4 3
    2 5];
y = pdist(a,'cityblock');       % 两两行向量之间的距离，绝对值距离'cityblock'
yc = squareform(y);             % 转为方阵
z = linkage(y);                 % 使用最短距离生成聚类图
dendrogram(z);                  % 画聚类图

 

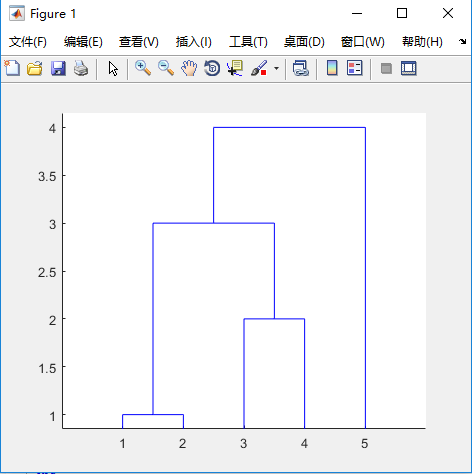
从图中其实分为几类已经明确了。

T = cluster(z,'maxclust',3);    % 对象分为3类
​
for i = 1:3
    tm = find(T==i);
    tm = reshape(tm,1,length(tm));
    fprintf('第%d类的有%s\n',i,int2str(tm));
end

 

 

R型聚类

Q型聚类可以是说，对对象物以类聚，人以群分，而R型聚类，是指对你评判的标准进行简化，也是按照Q型聚类的方法做的，只不过处理的对象不一样了而已。

栗子P225

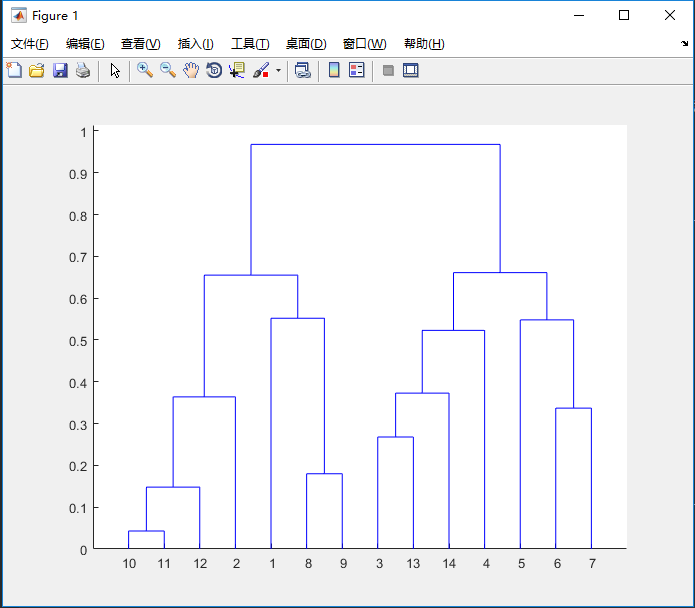
clc,clear;
a = textread('ch.txt');         % 相关系数矩阵
d = 1 - abs(a);                 % 转为距离矩阵
d = tril(d);                    % 提取下三角矩阵
​
b = nonzeros(d);                % 去0
b = b';                         % 聚类分析要行向量距离
​
z = linkage(b,'complete');      % 按最长距离聚类
h = dendrogram(z);              % 画聚类图