整数规划

整数规划

到整数规划了，可以说是线性规划的特殊情况，当然不能将整数规划的解直接取整得到。

解法有很多：

• 分支定界法

• 割平面（图解法）

• 隐枚举法

• 匈牙利法

• 蒙特卡洛法

这里主要讲计算机如何进行函数调用，哈哈！！！

 

0-1指派问题

模型：分配 n 人去做 n 项工作，每人做且仅做一项工作，若分配第 i 个人做第 j 项工作，需要花费 ​ 单位时间，

问如何分配使得工人花费的总时间最少。

变量 ​ 第 i 个人是否做第 j 项工作。

 

 

使用MATLAB解决决策问题，都需要转为一维决策向量，而lingo却不需要！扎心不。

函数调用：

​

 

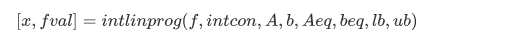
看上去A,b这两个不等式在0-1指派问题中好像并没有用到，最重要的是等式表达式Aeq,beq如何将二维决策转为一维决策问题。其实很巧妙，就是上面的约束条件中的两个等式，上下界是第3个等式。

直接上矩阵给你看看吧：

 

举个栗子P17：

clc, clear
c=[3 8 2 10 3;8 7 2 9 7;6 4 2 7 5
   8 4 2 3 5;9 10 6 9 10];
c=c(:); a=zeros(10,25); intcon=1:25;
for i=1:5
   a(i,(i-1)*5+1:5*i)=1;
   a(5+i,i:5:25)=1;
end
b=ones(10,1); lb=zeros(25,1); ub=ones(25,1);
x=intlinprog(c,intcon,[],[],a,b,lb,ub);

intcon 指的是整数变量的下标，这里5个变量(25个变量)均为整数。

混合整数规划

P18

这里的0-1部分就不是二维的啦，可以简单的套公式咯！！！

clc, clear
f=[-3;-2;-1]; intcon=3; %整数变量的地址
a=ones(1,3); b=7;
aeq=[4 2 1]; beq=12;
lb=zeros(3,1); ub=[inf;inf;1]; %x(3)为0-1变量
x=intlinprog(f,intcon,a,b,aeq,beq,lb,ub)