灰度预测

灰度预测

首先说，为啥要引出这个灰度预测，其实也就是在拟合的时候，效果不理想的一种另外的处理方案。

 

做灰度预测的步骤

 

P401，主要讨论G(1,1)模型

什么是G(1,1) 模型式一阶微分方程，且只含有1个变量的灰色模型。

 

举个栗子：

利用G(1,1) 模型预测某个城市道路交通噪声平均声级数。

 

数据的检验和处理

clc,clear;
x0 = [71.1 72.4 72.4 72.1 71.4 72.0 71.6]';
n = length(x0);
lamda = x0(1:n-1)./x0(2:n);     % 级比
range = minmax(lamda');
​
x1 = cumsum(x0);        % 累加
​
% 构造矩阵
B = [-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];
Y = x0(2:n);
​
% 公式计算,u(1) = a,u(2) = b
u = B\Y;

 

​

 

建立模型

嘿嘿，重点建模来了！！！

​

 

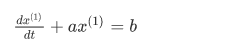
对其求解，公式好复杂！！！

​

 

注意哦，这里的x(1) 是预测值，符号打不出来了。然后疯狂代入k值就行了。

检验预测值

• 残差检验

• 相对误差

• 级比偏差

预测预报

 

 

附录

matlab程序

clc,clear;
x0 = [71.1 72.4 72.4 72.1 71.4 72.0 71.6]';
n = length(x0);
lamda = x0(1:n-1)./x0(2:n);     % 级比
range = minmax(lamda');
​
x1 = cumsum(x0);        % 累加
​
% 构造矩阵
B = [-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)];
Y = x0(2:n);
​
% 公式计算,u(1) = a,u(2) = b
u = B\Y;
​
% 微分方程预测
syms x(t)
x = dsolve( diff(x)+u(1)*x ==u(2) ,x(0) ==x0(1) );
xt = vpa(x,6);
yuce1 = subs(x,t,[0:n-1]);
yuce1 = double(yuce1);
yuce = [x0(1),diff(yuce1)];
​
%校验
epsilon = x0'-yuce;
delta = abs(epsilon./x0');
rho = 1 - (1-0.5*u(1)) / (1+0.5*u(1))*lamda';
 

 

 

好啦，G(1,1)模型ok了，但是你可以从他的表达式看出他是具有较强指数规律的序列，对于非单调的摆动序列和有饱和的S序列，采用G(2,1)模型。预测过程也是一样的。