数学基础——递推关系

问题1：兔子的繁殖

一对兔子在第二个月后才能产下一对新兔子。第n个月后有多少兔子。

分析：第n个月的兔子数f(n)，这f(n)个兔子可以分为两个部分，第一部分是上个月留下来的老兔子f(n-1)，

和新兔子，新兔子的数目是上个月有能力生育的兔子之和，也就是n-2天的兔子都有生育能力

 

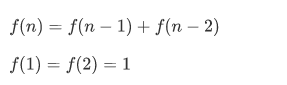
问题2：多边形的三角剖分。

给定一个凸n边形，把他分成三角形，求有多少种分法。

（和最优三角剖分类似，只不过不再是一个最值了，而是一个方案数）

 

问题3：火柴

用n个火柴可以拼成多少种不同的数字。火柴可以不必用完。

题目链接：https://uva.onlinejudge.org/external/113/11375.pdf

分析：

import java.math.BigInteger;
import java.util.Scanner;

public class Main {

    Main() {
        int c[] = { 6, 2, 5, 5, 4, 5, 6, 3, 7, 6 };
        BigInteger d[] = new BigInteger[2005];
        BigInteger sum[] = new BigInteger[2005];

        for (int i = 0; i <= 2000; i++) {
            d[i] = new BigInteger("0");
            sum[i] = new BigInteger("0");
        }

        d[0] = new BigInteger("1");

        for (int i = 0; i <= 2000; i++) {
            for (int j = 0; j < 10; j++) {
                if (!(i == 0 && j == 0) && i + c[j] <= 2000) {
                    d[i + c[j]] = d[i + c[j]].add(d[i]);
                }

            }
        }
        
        for(int i=1;i<=2000;i++) {
            sum[i] = sum[i].add(sum[i-1]);
            sum[i] = sum[i].add(d[i]);
        }

        Scanner in = new Scanner(System.in);
        while (in.hasNextInt()) {
            int n = in.nextInt();
            if (n == 0)
                System.out.println("0");
            else if (n < 6)
                System.out.println(sum[n]);
            else {
                System.out.println(sum[n].add(new BigInteger("1")));
            }
        }
    }
    

    public static void main(String[] args) {
        new Main();
    }
}

 

问题4：立方数之和

题目链接：https://uva.onlinejudge.org/external/111/11137.pdf

题意：给定一个数n ，求能够写成的立方形式有多少种。

分析：

就像DP种多阶段决策一样，d(i,j)，最大的元素为 i ，和为 j；题目已经给出 i <22;

那么：

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int n;
    unsigned long long d[22][10000+5];



    memset(d,0,sizeof(d));

    d[0][0] = 1;
    for(int i=1;i<=21;i++) {
        for(int j=0;j<=10000;j++) {
            for(int a=0;j+a*i*i*i<=10000;a++) {
                d[i][j+a*i*i*i] += d[i-1][j];
            }
        }
    }
    while(cin>>n)
        cout<<d[21][n]<<endl;

    return 0;
}

 

 

问题5：村民排队

题目链接：https://uva.onlinejudge.org/external/111/11174.pdf

题意：

村子里面有n个人来排队，里面有一些父子关系，儿子不能排到父亲的前面，有多少种排法？

分析：

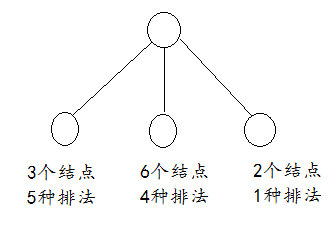
题目肯定是一个森林，设一个超级父亲节点，他下面如上图有三个子节点，

那么排法就有:

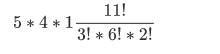
一般的：

设节点 i 为根的子树有f(i)种排法：

 

问题6：带标号的连通图的计数；

http://oeis.org/A001187

数列如上所示：

题目链接：http://poj.org/problem?id=1737

答案是f(n)，g(n) 是非联通图个数，那么就有 

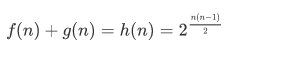
g(n)：先考虑1节点所在的连通分量包含哪些顶点：C(n-1,k-1)；

这个连通分量有f(k)，其他有h(n-k)种情况。

import java.math.BigInteger;
import java.util.Scanner;

public class Main {

    Main() {
        BigInteger two[] = new BigInteger[5055];
        two[0] = BigInteger.ONE;
        for (int i = 1; i <= 5050; i++)
            two[i] = two[i - 1].multiply(BigInteger.valueOf(2));
        BigInteger h[] = new BigInteger[55];
        for (int i = 1; i <= 50; i++) {
            h[i] = two[i*(i-1)/2];
        }
        
        BigInteger C[][] = new BigInteger[55][55];
        C[0][0] = BigInteger.ONE;
        for (int i = 0; i <= 50; i++) {
            C[i][0] = C[i][i] = BigInteger.ONE;
            for (int j = 1; j < i; j++) {
                C[i][j] = C[i - 1][j].add(C[i - 1][j - 1]);
            }
        }
        BigInteger f[] = new BigInteger[55];
        BigInteger g[] = new BigInteger[55];
        f[1] = BigInteger.ONE;
        for (int i = 2; i <= 50; i++) {
            g[i] = BigInteger.ZERO;
            for (int j = 1; j < i; j++) {
                g[i] = g[i].add(C[i - 1][j - 1].multiply(f[j]).multiply(h[i - j]));
            }
            f[i] = h[i].subtract(g[i]);
        }
        int n;
        Scanner cin = new Scanner(System.in);
        while (cin.hasNext()) {
            n = cin.nextInt();
            if (n == 0)
                break;
            System.out.println(f[n]);
        }
    }

    public static void main(String[] args) {
        new Main();
    }
}