LA 5713 秦始皇修路 MST

题目链接：http://vjudge.net/contest/144221#problem/A

题意：

秦朝有n个城市，需要修建一些道路使得任意两个城市之间都可以连通。道士徐福声称他可以用法术修路，不花钱，也不用劳动力，但只能修一条路，因此需要慎重选择用法术修哪一条路。秦始皇不仅希望其他道路的总长度B尽量短（这样可以节省劳动力），还希望法术连接的两个城市的人口之和A尽量大，因此下令寻找一个使得A/B最大的方案。你的任务是找到这个方案。

任意两个城市之间都可以修路，长度为两个城市之间的欧几里德距离。

 

分析：肯定是在最小生成树中删边，使得其他道路尽量短，又是添加哪两个点，使得人口最多。

就要枚举这两个点了，注意，架起来的桥，不一定是一定要删这两个点的边，而是，这两个点之间的路上的最大边。这样枚举就可以了。

那么就是要求每两个点之间的最大权了。(⊙o⊙)，这个dfs太精妙了，我想了好久，记录一下思想。

maxcost(i,j)点 i 和 j 之间的路里面的最大权，那么，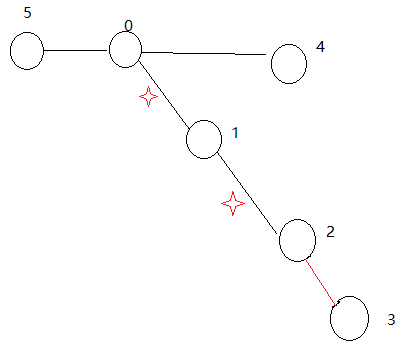

他等于是，他的新边，和之前的祖先的最优值。

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1000 + 10;

struct Edge
{
    int u,v;
    double d;
    bool operator < (const Edge& rhs) const
    {
        return d < rhs.d;
    }
};

int x[maxn];
int y[maxn];
int p[maxn];
int n;
Edge e[maxn*maxn];

vector<int> G[maxn];
vector<double> C[maxn];
int father[maxn];

int Find_Set(int x)
{
    if(x!=father[x])
        father[x] = Find_Set(father[x]);
    return father[x];
}

double MST()
{
    int m = 0;
    for(int i=0; i<n; i++)
    {
        for(int j=i+1; j<n; j++)
        {
            e[m++] = (Edge)
            {
                i,j,sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]))
            };
        }
    }
    sort(e,e+m);
    for(int i=0; i<n; i++)
    {
        father[i] = i;
        G[i].clear();
        C[i].clear();
    }
    int cnt = 0;
    double ans = 0;

    for(int i=0; i<m; i++)
    {
        int x = e[i].u;
        int y = e[i].v;
        int fx = Find_Set(x);
        int fy = Find_Set(y);

        double d = e[i].d;
        if(fx!=fy)
        {
            father[fx] = fy;
            G[x].push_back(y);
            C[x].push_back(d);
            G[y].push_back(x);
            C[y].push_back(d);
            ans += d;
            if(++cnt==n-1) break;
        }
    }
    return ans;
}

double maxcost[maxn][maxn];
vector<int> nodes;

// 0 -1 0
void dfs(int u, int fa, double facost)
{
    for(int i = 0; i < nodes.size(); i++)
    {
        int x = nodes[i];
        maxcost[u][x] = maxcost[x][u] = max(maxcost[x][fa], facost);
    }
    nodes.push_back(u);
    for(int i = 0; i < G[u].size(); i++)
    {
        int v = G[u][i];
        if(v != fa)
            dfs(v, u, C[u][i]);
    }
}


int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(int i=0; i<n; i++)
            scanf("%d%d%d",&x[i],&y[i],&p[i]);
        double tot = MST();

        memset(maxcost,0,sizeof(maxcost));
        nodes.clear();
        dfs(0, -1, 0);

        double ans = -1;

        for(int i=0; i<n; i++)
        {
            for(int j=i+1; j<n; j++)
            {
                ans = max(ans,(p[i]+p[j])/(tot-maxcost[i][j]));
            }
        }
        printf("%.2lf\n",ans);
    }

    return 0;
}