hiho一下,第115周,FF,EK,DINIC
题目1 : 网络流一·Ford-Fulkerson算法
描述
小Hi和小Ho住在P市,P市是一个很大很大的城市,所以也面临着一个大城市都会遇到的问题:交通拥挤。
小Ho:每到周末回家感觉堵车都是一种煎熬啊。
小Hi:平时交通也还好,只是一到上下班的高峰期就会比较拥挤。
小Ho:要是能够限制一下车的数量就好了,不知道有没有办法可以知道交通系统的最大承受车流量,这样就可以限制到一个可以一直很顺畅的数量了。
小Hi:理论上是有算法的啦。早在1955年,T.E.哈里斯就提出在一个给定的网络上寻求两点间最大运输量的问题。并且由此产生了一个新的图论模型:网络流。
小Ho:那具体是啥?
小Hi:用数学的语言描述就是给定一个有向图G=(V,E),其中每一条边(u,v)均有一个非负数的容量值,记为c(u,v)≥0。同时在图中有两个特殊的顶点,源点S和汇点T。
举个例子:
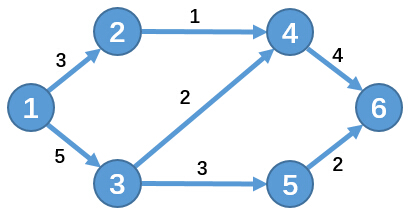
其中节点1为源点S,节点6为汇点T。
我们要求从源点S到汇点T的最大可行流量,这个问题也被称为最大流问题。
在这个例子中最大流量为5,分别为:1→2→4→6,流量为1;1→3→4→6,流量为2;1→3→5→6,流量为2。
小Ho:看上去好像挺有意思的,你让我先想想。
输入
第1行:2个正整数N,M。2≤N≤500,1≤M≤20,000。
第2..M+1行:每行3个整数u,v,c(u,v),表示一条边(u,v)及其容量c(u,v)。1≤u,v≤N,0≤c(u,v)≤100。
给定的图中默认源点为1,汇点为N。可能有重复的边。
输出
第1行:1个整数,表示给定图G的最大流。
提示:Ford-Fulkerson算法
小Hi:在你思考完成之前,我再给你讲一些网络流的性质好了。
对于任意一个时刻,设f(u,v)实际流量,则整个图G的流网络满足3个性质:
1. 容量限制:对任意u,v∈V,f(u,v)≤c(u,v)。
2. 反对称性:对任意u,v∈V,f(u,v) = -f(v,u)。从u到v的流量一定是从v到u的流量的相反值。
3. 流守恒性:对任意u,若u不为S或T,一定有∑f(u,v)=0,(u,v)∈E。即u到相邻节点的流量之和为0,因为流入u的流量和u点流出的流量相等,u点本身不会"制造"和"消耗"流量。
对于上面例子中的图,其对应的f网络图为(其中虚线表示实际不存在的边(v,u)):
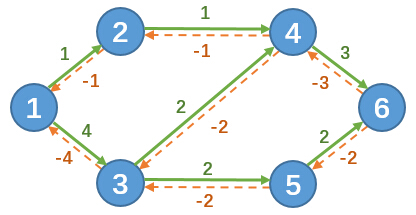
在此基础上,假设我们用cf(u,v)来表示c(u,v)-f(u,v),则可以表示每一条边还剩下多少的流量可以使用,我们称为残留容量。
假设一条边(u,v),其容量为3,使用了流量f(u,v)=2,则可以表示为:cf(u,v)=1, cf(v,u)=2。
由cf(u,v)构成的图我们称为残留网络。
比如例子中的残留网络图为:
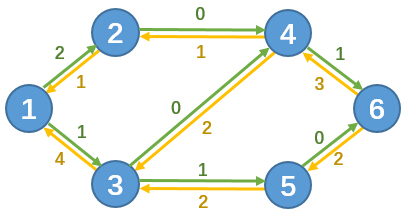
小Ho,你可以从残留网络作为着手点,会比较简单。
小Ho:残留网络,残留网络也就是可以使用的流量......我知道了!
既然残留网络表示还可以使用的流量,那么我就可以从图中找出一条从S到T的路径p,使得路径p上所有边的cf(u,v)都大于0。
假设路径p上最小的cf(u,v)等于k,那我就可以使得S到T增加k的流量。
小Hi:没错,通过该条路径p使得图G的最大流得到了增加,所以这样的路径p被称为增广路径。
小Ho:我大概有一个简单的算法了!
首先我根据读入的信息,就可以得到最初的图G,然后将其转化为残留网络。
接下来我在残留网络上寻找是否有增广路径,如果不存在增广路径,则说明这个图不能再增加流量了。
若存在增广路径,则我将最大流量增加,同时对增广路径上的边cf(u,v)进行修改,再重复寻找增广路径。
整个过程大概就是:
While ( findAugmentPath() ) // 判断是否有增广路 maxFlow = maxFlow + delta // 最大流增加 modifyGraph() // 对增广路进行修改 End While
小Hi:那么你打算怎么实现寻找增广路和修改路径呢?
小Ho:寻找增广路的话,直接使用BFS从源点S开始搜索,记录每个点的路径以及路径上的最小残余容量:
findAugmentPath(): queue = [] // 重置搜索队列 path = [] // 初始化路径数组为0 capacity = [] // 初始化流量数组为0 visited = [] // 初始化访问数组为false tail = 0 queue[ tail ] = S // 将源点加入队列 capacity[S] = ∞ // 到源点的流量为无穷大 visited[S] = true i = 0 While (i ≤ tail) u = queue[i] If (u == T) Then // 已经找到一条增广路 Return capacity[T] End If For (u, v)∈残留网络 and cf(u,v)>0 and not visited[v] // u到v有残留容量,且v未被访问过 path[v] = u // 记录路径 capacity[v] = min(cf(u,v), capacity[u]) // 记录路径上的最小残余容量 visited[v] = true tail = tail + 1 queue[ tail ] = v End For i = i + 1 End While
而对于路径的修改,在已经有path数组的情况下,利用迭代或者回溯都可以完成:
modifyGraph(): flow = capacity[T] now = T While ( now is not S ) fa = path[ now ] cf(fa, now) = cf(fa, now) - flow cf(now, fa) = cf(now, fa) + flow // 反向的残余容量是增加 now = fa End While
小Ho:时间复杂度方面,每一次寻找增广路的时间为O(n+m),每一次修改路径的时间复杂度为O(n)。假设图的最大流为maxflow,那么我的算法时间复杂度为O((n+m)*maxflow)。
小Hi:嗯,你所采用的算法就是最简单的最大流解决办法,最早是由L.R.Ford和D.R.Fulkerson在1956年时发表,因此也被称为Ford-Fulkerson算法。对于第一次接触网络流而言,可以先试着实现这个算法,对于你理解网络流会有很大的帮助。
小Ho:不过小Hi,我有一个小疑问,虽然我直观上感觉找不到新的增广路时就已经是最大流了,但这真的没有问题么?
小Hi:找不到增广路确实是等价于找到最大流,不过具体的证明嘛,请听下回分解。
看了一下这个Ford-Fulkerson算法,感觉和EK很相似,都是BFS不断增广。
然后,我当时有个数组没有开足够,竟然是TLE,后来学了一下Dinic算法。
这里总结一下这3个算法:
Ford-Fulkerson: 也是最初的最大流算法,简单讲就是,不断DFS增广,直到找不到增广路。
Edmonds-Karp:是FF的变形,不断BFS增广,直到找不到增广路。
Dinic:BFS分层,DFS增广。

#include <bits/stdc++.h> using namespace std; #define maxn 505 #define INF 0x3f3f3f3f struct Edge { int from,to,cap,flow; }; struct Dinic { int n,m,s,t; vector<Edge> edge; vector<int> G[maxn]; bool vis[maxn]; int d[maxn]; int cur[maxn]; void addEdge (int from,int to,int cap) { edge.push_back((Edge){from,to,cap,0}); edge.push_back((Edge){to,from,0,0}); m = edge.size(); G[from].push_back(m-2); G[to].push_back(m-1); } bool BFS() { memset(vis,0,sizeof(vis)); queue<int> Q; Q.push(s); d[s] = 0; vis[s] = 1; while(!Q.empty()) { int x = Q.front(); Q.pop(); for(int i=0; i<G[x].size(); i++) { Edge & e = edge[G[x][i]]; if(!vis[e.to]&&e.cap>e.flow) { vis[e.to] = 1; d[e.to] = d[x] + 1; Q.push(e.to); } } } return vis[t]; } int DFS(int x,int a) { if(x==t||a==0) return a; int flow = 0,f; for(int & i = cur[x]; i<G[x].size(); i++) { Edge & e = edge[G[x][i]]; if(d[x] + 1==d[e.to]&&(f=DFS(e.to,min(a,e.cap-e.flow)))>0) { e.flow +=f; edge[G[x][i]^1].flow -=f; flow +=f; a-=f; if(a==0) break; } } return flow; } int Maxflow (int s,int t) { this->s = s;this->t = t; int flow = 0; while(BFS()) { memset(cur,0,sizeof(cur)); flow+=DFS(s,INF); } return flow; } }sol; int main() { int n,m; scanf("%d%d",&n,&m); for(int i=0;i<m;i++) { int u,v,cap; scanf("%d%d%d",&u,&v,&cap); sol.addEdge(u,v,cap); } printf("%d\n",sol.Maxflow(1,n)); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号