欧拉函数学习笔记
读前警告:本文 MD 以及 \(\LaTeX\) 差到爆炸,因为是直接复制的。
首先,\(\varphi(n)\) 的值是小于 \(n\) 且与 \(n\) 互质的数的个数。


//求n的欧拉函数值: phi[n]
int getPhi(int n){
int ans = n;
for(int i = 2; i*i <= n; i++){
if(n % i == 0){
ans = ans * (i-1)/i;
while(n % i == 0) n /= i;
}
}
if(n > 1) ans = ans * (n-1)/n ;
return ans;
}
时间复杂度:sqrt(n)
其实,它还可以用一个叫做“积性函数”的东西拿线性筛求 \(1\) 到 \(n\) 的 \(\varphi\) 值!

下面这张里面的 \(\phi\) 和 \(\varphi\) 是一个东西(在公式里面是 \phi 和 \varphi)
然后那堆歪歪斜斜甚至弯的都是 \(1\)(指都是 \(\frac{1}{p_i}\))

若 \(q\) 是质数,且 \(n\bmod q=0\),则 \(\varphi(nq)=q\varphi(n)\);若 \(q\) 是质数,且 \(n \bmod q \neq 0\),则 \(\varphi(nq)=(q-1)\varphi(n)\)。
啊上面那个结论你直接看 \(\varphi(n)\) 的计算式不就一眼顶针了(
对了特别提一嘴 \(\varphi(1)=1\)。
线性筛求 $\varphi$
//n是数据范围
memset(ip,1,sizeof(ip));
ip[1]=0;
phi[1]=1;
rep(i,2,n,1)
{
if(ip[i])
{
p[++tot]=i;
phi[i]=i-1;
}
for(LL j=1;j<=tot&&i*p[j]<=n;j++)
{
LL x=i*p[j];
ip[x]=0;
if(i%p[j]!=0)phi[x]=(p[j]-1)*phi[i];
else
{
phi[x]=p[j]*phi[i];
break;
}
}
}
你可能会问:你这玩意除了装X还有个【数据删除】用?
欸嘿还真不是,来了题你就知道了
T1
给定整数N和M,有多少整数X满足1<=X<=N且gcd(X,N)>=M?
第一行输入是一个整数T(T<=100),表示测试用例的数量。以下T行各包含两个数字N和M(2<=N<=100000000,1<=M<=N),表示一个测试用例。(注意这是个伏笔)
首先 \(N\) 最多有 \(\sqrt n\) 个因数(说实话大多数时间达不到这个上限)
设 \(d\) 是 \(N\) 的约数,且 \(d>=M\)。
其实它起的不是约数的作用,而是这个最大公因数!因为不管咋样 \(\gcd(N,X)\mid N\)。
枚举它,问题就成了 \(1\) 到 \(\frac{n}{d}\) 有多少数和 \(\frac{n}{d}\) 互质(\(\frac{n}{d}\) 即 \(X\))。
欸这好像是 \(\varphi(\frac{n}{d})\) 欸!
然后就水了,直接求和。
对了记得伏笔吗?这个 \(\varphi\) 不能线性筛求,得用它自己的计算公式。
代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define lowbit(x) ((x)&(-(x)))
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
LL phi(LL n)
{
LL sum=n;
for(LL i=2;i*i<=n;i++)
{
if(n%i==0)
{
sum=sum*(i-1)/i;
while(n%i==0)n/=i;
}
}
if(n>1)sum=sum*(n-1)/n;
return sum;
}
LL t,n,m,p[100010],o;
int main()
{
cin>>t;
while(t--)
{
cin>>n>>m;
LL sum=0;
o=0;
for(LL i=1;i*i<n;i++)
{
if(n%i==0)
{
p[++o]=i;
p[++o]=n/i;
}
}
LL s=sqrt(n);
if(s*s==n)p[++o]=s;
rep(i,1,o,1)
{
if(p[i]>=m)sum+=phi(n/p[i]);
}
cout<<sum<<endl;
}
return 0;
}
T2
给定一个正整数N,你的任务是计算小于N且和N不互质的正整数的和。如果A,B除了1之外没有公共的正约数,则称A与B互质。
考虑补集,求出所有互质的数的总和。
利用欧拉函数和欧几里德定理,可知若 \(\gcd(n,i)=1\) 则 \(\gcd(n,n-i)=1\)。
于是乎所有与 \(n\) 互质的数的和为 \(\frac{n\times \varphi(n)}{2}\)(和为 \(n\),有 \(\frac{\varphi(n)}{2}\) 对)
那不互质的就是 \(\frac{n\times (n-1)-n\times \varphi(n)}{2}\)。
代码
#include<stdio.h>
#include<bits/stdc++.h>
#define MOD 1000000007
#define LL long long
using namespace std;
LL phi(LL n)
{
LL sum=n;
for(LL i=2;i*i<=n;i++)
{
if(n%i==0)
{
sum=sum*(i-1)/i;
sum%=MOD;
while(n%i==0)n/=i;
}
}
if(n>1)sum=sum*(n-1)/n;
sum%=MOD;
return sum;
}
LL n;
int main()
{
cin>>n;
while(n!=0)
{
cout<<(n*(n-1)/2%MOD-phi(n)*n/2%MOD+MOD)%MOD<<endl;
cin>>n;
}
return 0;
}
T3
洛谷P2303
暴力硬拆!!!!
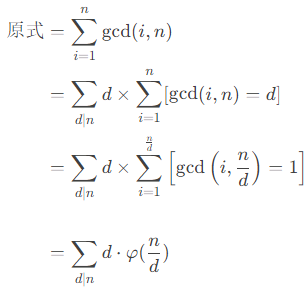
爆枚 \(n\) 因数!!!
爆算 \(\varphi(\frac{n}{d})\)!!!!
代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define lowbit(x) ((x)&(-(x)))
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
LL phi(LL n)
{
LL sum=n;
for(LL i=2;i*i<=n;i++)
{
if(n%i==0)
{
sum=sum*(i-1)/i;
while(n%i==0)n/=i;
}
}
if(n>1)sum=sum*(n-1)/n;
return sum;
}
LL t,n;
int main()
{
cin>>n;
LL sum=0;
for(LL i=1;i*i<=n;i++)
{
if(n%i==0)
{
sum+=i*phi(n/i);
if(i*i!=n)sum+=(n/i)*phi(i);
}
}
cout<<sum<<endl;
return 0;
}
T4
洛谷P2158
这题名字挺魔怔的对我来说(
因为我们班有个同学之前每次跑操都跑到前面转手,伸直胳膊,说这是殡仪馆仪仗队(
好了不闹了。
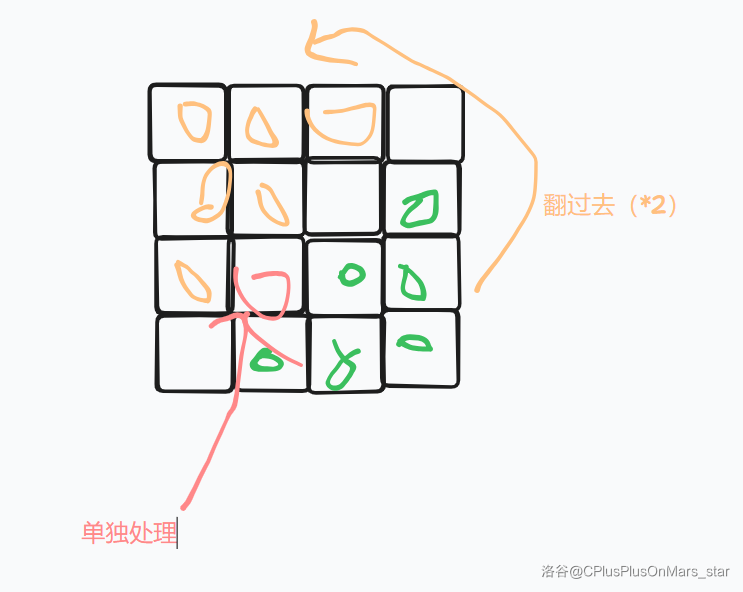
能被看到,需要啥?
欸你想啊,如果 \(x\) 和 \(y\)(行号和列号)不互质,那他不就被 \((\frac{x}{\gcd(x,y)},\frac{y}{\gcd(x,y)})\) 那里的人挡住了吗?
想不到的,以斜率代之
他俩是同一个方向的!
那只需要算 \(x\) 和 \(y\) 互质的个数了!
如果你还问怎么求给我从头再看一次!
拿欧拉函数啊!
突然冥冥之中有人大声对你喊:
你回去看一眼欧拉函数,\(\varphi(n)\) 是小于 \(n\) 且与 \(n\) 互质的数的个数!!!!!
其实你算一半,然后 \(\times 2+1\) 不就解决了!
这个 \(+1\) 是因为 \((2,2)\) 也能看到,只算左右半会漏掉。
如图所示:
但是要有一个特判!
\(N=1\) 时答案是 \(0\)!
就自己一个,你还看不到自己,所以是 \(0\)。
代码
#include<stdio.h>
#include<bits/stdc++.h>
#define LL long long
using namespace std;
LL n,pi[40010],p[40010],sum,o;
bool ip[40010];
int main()
{
cin>>n;
pi[1]=1;
for(int i=2;i<=n;i++)
{
if(!ip[i])
{
p[++o]=i;
pi[i]=i-1;
}
for(int j=1;j<=o&&i*p[j]<=n;j++)
{
ip[i*p[j]]=1;
if(i%p[j]==0)
{
pi[i*p[j]]=pi[i]*p[j];
break;
}
else pi[i*p[j]]=pi[i]*pi[p[j]];
}
}
for(int i=1;i<n;i++)sum+=pi[i];
cout<<(n==1?0:sum*2+1)<<endl;
return 0;
}
T5
洛谷P2568
枚举一个质数 \(p\),以及 \(x=a\times p,y=b\times p\),然后就变成了求 \(1\le a,b\le \frac{N}{p}\) 内有多少对 \((a,b)\) 互质了啊!
然后这玩意是个人都想得到用 \(\varphi\)。
假设 \(a<b\),sum+=phi[1]+phi[2]+...+phi[N/p]
但是有个点!你注意到我们的假设了吗!记得 \(\times 2\)!
对了 phi[1] 不用翻倍因为他能干的只有 \((1,1)\) 一个(笑
然后要前缀和。
代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define lowbit(x) ((x)&(-(x)))
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
LL n,tot,p[10000010],phi[10000010],c[10000010],sum;
bool ip[10000010];
int main()
{
memset(ip,1,sizeof(ip));
ip[1]=0;
phi[1]=1;
cin>>n;
rep(i,2,n,1)
{
if(ip[i])
{
p[++tot]=i;
phi[i]=i-1;
}
for(LL j=1;j<=tot&&i*p[j]<=n;j++)
{
LL x=i*p[j];
ip[x]=0;
if(i%p[j]!=0)phi[x]=(p[j]-1)*phi[i];
else
{
phi[x]=p[j]*phi[i];
break;
}
}
}
rep(i,2,n,1)
{
c[i]=c[i-1]+phi[i];
}
rep(i,1,tot,1)
{
sum+=phi[1]+2*c[n/p[i]];
}
cout<<sum<<endl;
return 0;
}
T6
洛谷P2398
首先考虑洛谷P1390。
我们拿线性筛,求出 \(\varphi(1)\) 到 \(\varphi(n)\)。
搞个前缀和:sum[i]=phi[1]+...+phi[i]。
wait!
只有一个数不合法!
所以是:sum[i]=phi[1]+...+phi[i]。
然后我们枚举个 \(d\),它是最大公约数,然后你求 \(d\times \sum\limits_{i=2}^{n/d}\) 也就是 d*sum[d] 就是最大公约数为 \(d\) 时的答案。
最终答案就是 \(\sum\limits_{d=1}^{n}d\times sum(\frac{n}{d})\)。
然后因为洛谷P2398的答案相当于洛谷P1390的答案 \(\times 2\)(因为可以两个数调过来)再 \(+\sum\limits_{k=1}^{n}k\)(\(i=j\) 时)。
代码
#include<stdio.h>
#include<bits/stdc++.h>
#define N 1000010
#define MOD 998244353
#define esp 1e-8
#define INF 999999999999999999
#define LL long long
#define rep(i,a,b,g) for(LL i=a;i<=b;i+=g)
#define rem(i,a,b,g) for(LL i=a;i>=b;i-=g)
#define repn(i,a,b,g) for(LL i=a;i<b;i+=g)
#define remn(i,a,b,g) for(LL i=a;i>b;i-=g)
#define pll pair<LL,LL>
#define mkp(x,y) make_pair(x,y)
#define lowbit(x) ((x)&(-(x)))
#define i128 LL
#define lc (u<<1)
#define rc (u<<1|1)
using namespace std;
void read(i128 &x)
{
i128 f=1;
x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
x*=f;
}
void write(i128 x)
{
if(x>=10)write(x/10);
putchar(x%10+'0');
}
LL n,tot,p[4000010],phi[4000010],sum[4000010],c[4000010],ffff[4000010];
bool ip[4000010];
int main()
{
memset(ip,1,sizeof(ip));
ip[1]=0;
phi[1]=1;
rep(i,2,200000,1)
{
if(ip[i])
{
p[++tot]=i;
phi[i]=i-1;
}
for(LL j=1;j<=tot&&i*p[j]<=200000;j++)
{
LL x=i*p[j];
ip[x]=0;
if(i%p[j]!=0)phi[x]=(p[j]-1)*phi[i];
else
{
phi[x]=p[j]*phi[i];
break;
}
}
}
rep(i,2,200000,1)
{
c[i]=c[i-1]+phi[i];
}
LL summ=0;
read(n);
rep(i,1,n,1)
{
summ+=i*c[n/i];
}
write(summ*2+n*(n+1)/2);
return 0;
}
小结
\(\varphi\) 真的很好用。
以后还可以逆元。
以后我肯定是要写逆元学习笔记的,大家等着就行!



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· AI技术革命,工作效率10个最佳AI工具