UVA10089 Repackaging

设第 \(i\) 种包装中 \(j\) 尺寸的杯子数量为 \(S_{ij}\)，第 \(i\) 种包装选取的数量为 \(a_i\)，若能够按照要求进行重新打包，有

\[\begin{cases} a_1S_{11} + a_2S_{21} + \cdots + a_nS_{n1} = k \\ a_1S_{12} + a_2S_{22} + \cdots + a_nS_{n2} = k \\ a_1S_{13} + a_2S_{23} + \cdots + a_nS_{n3} = k \\ \end{cases} \]

其中 \(k \in \mathbb{N}^+\)。
相邻两式相减，得

\[\begin{cases} a_1(S_{11} - S_{12}) + a_2(S_{21} - S_{22}) + \cdots + a_n(S_{n1} - S_{n2}) = 0 \\ a_1(S_{12} - S_{13}) + a_2(S_{22} - S_{23}) + \cdots + a_n(S_{n2} - S_{n3}) = 0 \\ \end{cases} \]

记 \(\vec{S_i} = (S_{i1} - S_{i2}, S_{i2} - S_{i3})\)， 则

\[\sum_{i = 1}^{n}a_i\vec{S_i} = \vec{0} \]

下证：若干向量之和为 \(\vec{0} \iff\) 任意两相邻向量间的夹角不大于 \(\pi\)。
注：此处定义的夹角与常见的向量夹角的定义不同。此处定义向量 \(\vec{a}, \vec{b}\) 之间的夹角 \((\vec{a}, \vec{b})\) 为从 \(\vec{a}\) 逆时针旋转到 \(\vec{b}\) 的角。\((\vec{a}, \vec{b}) + (\vec{b}, \vec{a}) = 2\pi\)。

必要性：若存在两相邻向量夹角大于 \(\pi\)，必存在一条直线，可以使得所有的向量都在其一侧。如此，所有的向量之和必然会有沿垂直于该直线方向的分量，不可能为 \(\vec{0}\)。

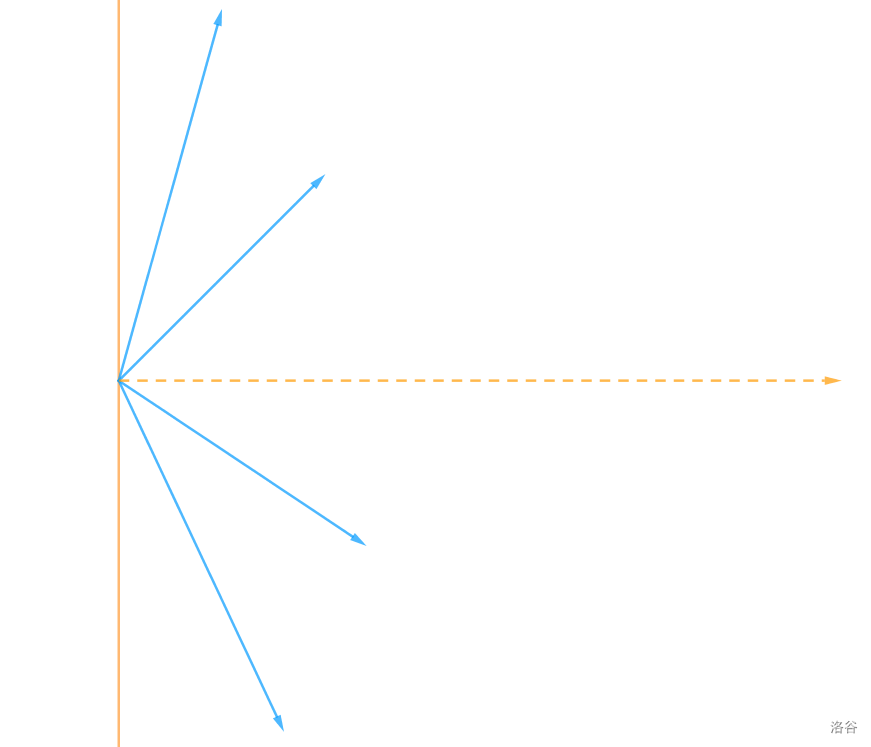
充分性：不妨考虑 \(3\) 个向量的情况。选取适当的 \(a_i\)，可以使得这 \(3\) 个向量首尾相接形成三角形，即和为 \(\vec{0}\)。

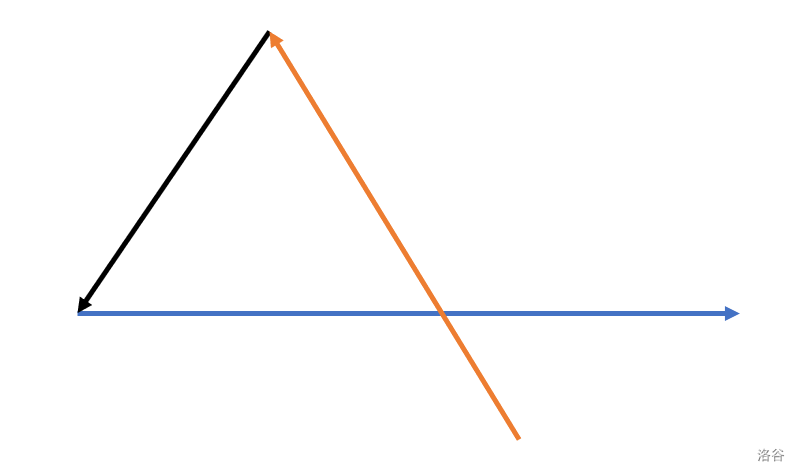
下证：从 \(3\) 个以上任意两相邻向量间的夹角不大于 \(\pi\) 的向量中，总可以选取出 \(3\) 个任意两相邻向量间的夹角夹角小于 \(\pi\) 的向量。
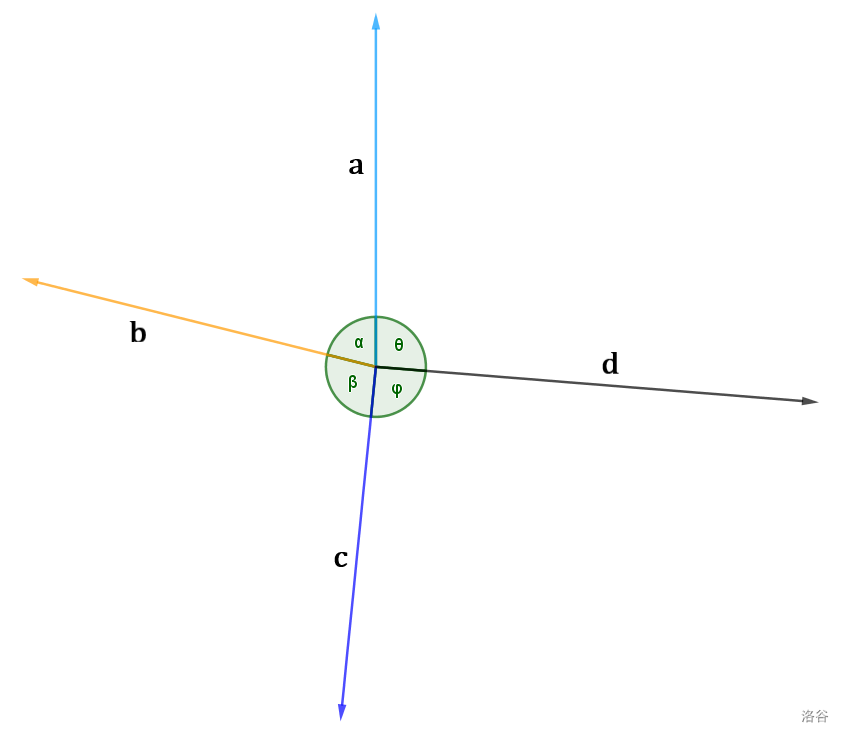
证明：假设无法取得。不妨设 \(\vec{a}, \vec{b}, \vec{c}\) 是任取的三个向量，其中 \((\vec{c}, \vec{a}) > \pi\)。由于任意两相邻向量间的夹角不大于 \(\pi\)，\(\vec{c}, \vec{a}\) 之间必存在一向量 \(\vec{d}\)，\((\vec{c}, \vec{d})\) 和 \((\vec{d}, \vec{a})\) 都小于 \(\pi\)。如图，将四个角分别记作 \(\alpha, \beta, \varphi, \theta\)。因为无法选取出 3 个任意两相邻向量间的夹角夹角小于 \(\pi\) 的向量，所以用 \(\vec{d}\) 取代 \(\vec{a}, \vec{b}, \vec{c}\) 中任何一个后，仍然会存在两相邻向量夹角大于 \(\pi\)。故有

\[\begin{cases} \alpha + \theta > \pi \\ \beta + \varphi > \pi \\ \alpha +\beta > \pi \\ \theta + \varphi > \pi \\ \end{cases} \]

相加后化简得 \(\alpha + \beta + \theta + \varphi > 2\pi\)，与 \(\alpha + \beta + \theta + \varphi = 2\pi\) 矛盾。

如此，当向量个数大于 \(3\) 个时，可以从中选取 \(3\) 个两两夹角小于 \(\pi\)的向量，令其余向量对应的 \(a_i = 0\)，便转化到了 \(3\) 个向量的情况。

综上所述，只需将这些向量排序后依次判断相邻两向量夹角是否都不大于 \(\pi\)，即可判断是否有解。需要注意的是，排序后的第 \(n\) 个向量与第一个向量也是相邻的。
代码如下

#include <stdio.h>
#include <algorithm>
typedef long long ll;

struct point{
    ll x, y;
    int quad;
    ll operator * (const point &t) const {
        return x * t.y - t.x * y;
    }
    bool operator < (const point &t) const {
        return quad == t.quad ? *this * t > 0 : quad < t.quad;
    }
};
point a[1010];

int quad(point p) {
    if (p. x == 0) {
        if (p.y > 0) return 3;
        else return 7;
    } else if (p.x > 0) {
        if (p.y > 0) return 2;
        else if (p.y == 0) return 1;
        else return 8;
    } else {
        if (p.y > 0) return 4;
        else if (p.y == 0) return 5;
        else return 6;        
    }
}

int n;

int main() {
    while (~scanf("%d", &n) && n) {
        for (int i = 1; i <= n; ++i) {
            ll x, y, z;
            scanf("%lld%lld%lld", &x, &y, &z);
            a[i].x = x - y, a[i].y = (y - z);
            a[i].quad = quad(a[i]);
        }
        std::sort(a + 1, a + n + 1);
        bool flag = false;
        for (int i = 1; i < n; ++i) {
            if (a[i] * a[i + 1] < 0) {
                printf("No\n");
                flag = true;
                break;
            }
        }
        if (flag) continue;
        if (a[n] * a[1] < 0) printf("No\n");
        else printf("Yes\n");
    }
    return 0;
}