测地极坐标参数化纹理贴图

　　1.和离散参数化一样，还是对网格模型选取一基准顶点 Vi，以最短路径dijkstra算法广度遍历，记录其他顶点到基准顶点的路径

　　2.对于除了基准顶点之外的顶点，其测地极坐标下的纹理坐标计算分为两类：一环邻域，非一环邻域。

　　A.一环邻域：

　　对于网格曲面的任意一点S，根据S位于网格三角面片的位置，可以分为 内点、边点、顶点。

　　a.若是内点，直接映射便可

　　b.若是边点，则固定其中一个三角面片为基准平面，以S所在边为轴承，旋转另一三角面片到基准平面，如图

　　

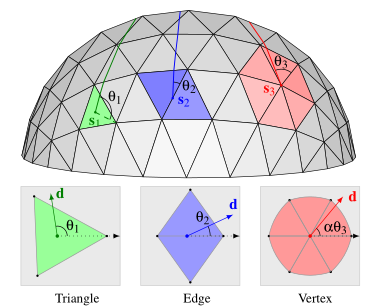
　　c.若是顶点，则做展平参数化，如图

　　

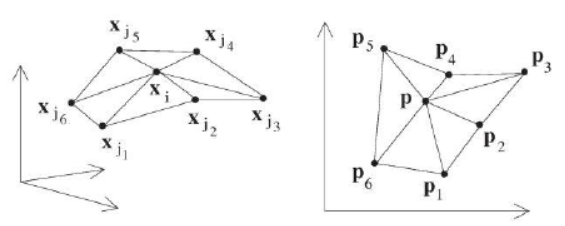
　　三维空间中的顶点 Xi, 周围一环邻域的顶点(Xj1, Xj2……)，将其映射到平面上，满足条件：

　　

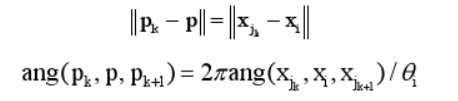
　　B.非一环邻域

　　已知 S 为基准点，顶点 Vj, Vk的测地坐标为（Rj, θj）、（Rk, θk）。要求取顶点 Vi 的测地坐标。

　　按照步骤 A 中的步骤 c ，将Vi 以及其一环邻域顶点做展平化处理，如图

　　　

　　此时，顶点 Vi , Vj , Vk 在同一平面，顶点 Vj，Vk 分别以自身测地坐标极径Rj , Rk，为半径画圆，两圆相交于点 S ‘，以S ‘ 为伪基准点求取 Vi 的测地极坐标。

　　

　　

　　Vi 的测地坐标极径为：

　　

　　Vi 的测地坐标极角为：

　　

　　α=ϕij/ϕkj .

 

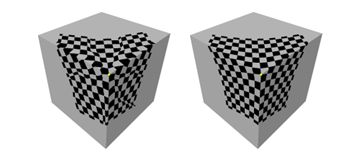
　　离散指数映射和测地极坐标参数化对比

 

　　

 

　　参考文献：

　　Geodesic Polar Coordinates on Polygonal Meshes

　　三角网格平面参数化的研究

　　http://blog.csdn.net/hjimce/article/details/46489899