NOIP培训Day9 [3]苦恼的小明

苦恼的小明

(worry.c  worry.pas  worry.cpp)

时限1秒

描述：

黄小明和他的合伙人想要创办一所英语培训机构，注册的时候要填一张个人情况的表格，在身高一栏小明犯了愁。

身高要求精确到厘米，但小明实在太高了，无法在纸上填下这么长的数字。小明花钱买通了办事人员，于是只要写上他的身高模10007的结果就行了。

可小明不会取模，想起前几天请你帮他解决了水库的问题，于是又来找你帮忙。

输入：（worry.in)

小明的身高用A1^A2^...^An表示，第一行输入n，第二行输入n个正整数表示A1至An。

输出：（worry.out)

一个数字表示小明身高mod 10007的值。

样例输入：                                      样例输出：

2                                                      173

17 747

数据范围：

所有的0<=Ai<10000

第1~6数据点满足n=2

第7~10数据点满足n=3

第11个数据点满足n=1234567

（前六个数据会逐渐变大，照顾一下取模没弄清楚的同学。另外没有必要尝试对a1进行0或1的判断来骗分，估计是骗不到的。当然了，如果自认为运气好的人可以试试看，我也阻止不了你。）

题解：

      这题其实不难，关键是你要弄明白欧拉函数。

==========================================wikipedia==========================================

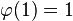\varphi(1)=1（小于等于1的正整数中唯一和1互质的数就是1本身）。

若n是质数p的k次幂，\varphi(n)=\varphi(p^k)=p^k-p^{k-1}=(p-1)p^{k-1}，因为除了p的倍数外，其他数都跟n互质。

欧拉函数是积性函数，即是说若m,n互质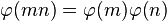，\varphi(mn)=\varphi(m)\varphi(n)。证明：设A, B, C是跟m, n, mn互质的数的集，据中国剩余定理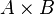，A \times B和C可建立双射(一一对应)的关系。因此\varphi(n)的值使用算术基本定理便知，

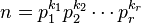
若n = p_1^{k_1} p_2^{k_2} \cdots p_r^{k_r}
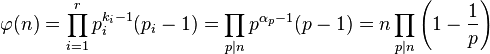则\varphi(n) = \prod_{i=1}^r p_i^{k_i-1}(p_i-1) = \prod_{p\mid n} p^{\alpha_p-1}(p-1) = n\prod_{p|n}\left(1-\frac{1}{p}\right)。

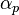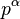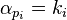其中\alpha_p是使得p^{\alpha}整除n的最大整数\alpha（这里\alpha_{p_i} = k_i）。

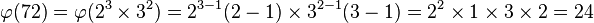
例如\varphi(72)=\varphi(2^3\times3^2)=2^{3-1}(2-1)\times3^{2-1}(3-1)=2^2\times1\times3\times2=24

=========================================================================================

所以，我们可以用欧拉函数加上快速幂，来解决这一道题目。

具体代码实现：(By Tony)

/*
 * Number theory Problem  -  Eulers Function
 * Code By TonyFang
 * Mail To tony-fang@foxmail.com
 * Copyright TonyFang (in CodeForces) 2013
 * All rights reserved.
 * Copyright TonyFang 2000-2013 (now)
 * All rights reserved.
 * worry.cpp   /    input:worry.in     /     output:worry.out
 */
# include <iostream>
# include <stdio.h>
# include <stdlib.h>
# include <string.h>
# include <math.h>
# include <algorithm>
using namespace std;
const int MODN = 10007;
const int MAXN = 1234568;
/*快速幂*/ 
int POWER(int a,int n,int MO) {
	int ret = 1, base = a;
	while(n != 0) {
		if(n & 1) {
			ret *= base;
			ret %= MO;
		}
		base *= base;
		base %= MO;
		n >>= 1;
	}
	return ret % MO;
}
int main() {
	freopen("worry.in","r",stdin);
	freopen("worry.out","w",stdout);
	/*动态内存分配，节省空间*/ 
	int n,ans,*a,*p,*l;
	a = new int [MAXN];
	p = new int [MODN];
	l = new int [MAXN];
	memset (p,0,sizeof(p));
	memset (l,0,sizeof(l));
	/*读取*/ 
	scanf("%d",&n);
	for (int i = 1;i <= n;i ++)
		scanf("%d",&a[i]);
	p[1] = 1;
	/* 欧拉函数 */ 
	for (int i = 2;i <= MODN;i ++)
		if (! p[i])
			for (int j = i;j <= MODN;j += i) {
				if (!p[j]) p[j]=j;
				p[j]=p[j]/i*(i-1);
			}
	l[1] = MODN;
	for (int i = 2;i <= n - 1;i ++) 
		l[i] = p[l[i - 1]];
	/* 计算幂(使用快速幂) */ 
	for (int i = n - 1;i >= 1;i --)
		a[i] = POWER(a[i],a[i + 1],l[i]) + l[i];
	printf("%d\n",a[1] % MODN);
	/*删除已分配的动态内存*/ 
	delete []a;
	delete []p;
	delete []l;
	return 0;
}

 

posted @ 2013-07-19 18:51  TonyFang  阅读(451)  评论(0)  编辑  收藏  举报