UVA11021 Tribles

UVA11021 Tribles

Solution

说是全概率公式推导出来个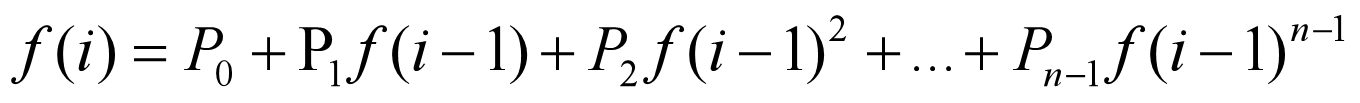

大体理解下， 首先假设 f[i - 1] 已知嘛
那他可以从多少种情况转移过来咧

一共不是死一只、两只。。。n - 1只嘛
所以它其实是用第一个状态推过来的， 第一个生一只， 死完的概率是 f[i - 1]
两只是 f[i - 1] ^ 2
就这么推出来了

Code

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#include<climits>
#include<cmath>
#define LL long long
#define REP(i, x, y) for(int i = (x);i <= (y);i++)
using namespace std;
int RD(){
    int out = 0,flag = 1;char c = getchar();
    while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}
    while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}
    return flag * out;
    }
const int maxn = 1010;
int T, num, k, m, Tony;
double p[maxn];
double dp[maxn];
void init(){
	num = RD(), k = RD(), m = RD();
	REP(i, 0, num - 1)cin>>p[i];
	dp[1] = p[0];
	}
void work(){
	REP(i, 2, m){
		double res = 1;
		dp[i] = 0;
		REP(j, 0, num - 1){
			dp[i] += res * p[j];
			res *= dp[i - 1];
			}
		}
	printf("Case #%d: %.7f\n", ++Tony, pow(dp[m], k));
	}
int main(){
	T = RD();
	while(T--){
		init();
		work();
		}
	return 0;
	}