LG P9108 [PA2020] Malowanie płotu

状态数是 \(O(nm^2)\) 的DP很好想，就是 \(dp_{i,l,r}\) 表示第 \(i\) 次的区间为 \([l,r]\) 的方案数。

但是这个状态数就已经死了，而题目又提示 \(n\times m \leq 1e7\) ，说明状态只能形如 \(dp_{i,j}\)。

这时就会想到一个简陋的打补丁方式：设 \(f_{i,l},g_{i,r}\) 分别表示第 \(i\) 次以 \(l\) 为左端点的所有区间的方案数，以 \(r\) 为右端点的所有区间的方案数。

因为 \(f,g\) 本质相同，所以下面都只关注 \(f\)。

设第 \(i\) 个区间为 \([l,r]\)，第 \(i-1\) 个为 \([l',r']\)。那么两者相交的话，有以下四种情况。

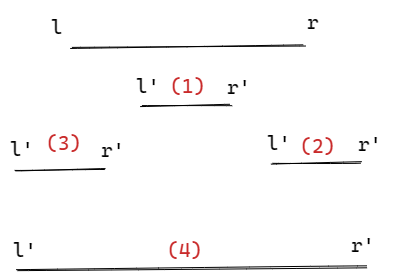
方便表述，起个简称：包含，左交，右交，被包含（主语是第 \(i\) 个区间）。

我们希望求出 \(f_{i,l}\)，那么先暴力地转移。那么枚举右端点 \(r\)，对于1，2种，直接 \(f_{i-1,l\textcolor{red}<l'\leq r} \to f_{i,l}\)。

那么3，4种呢？如果仿照刚刚直接把右端点 \(\geq r\) 的 \(g_{i-1}\) 全部加入，那么会有些区间算重复。

观察3，4有没有1，2没有的性质用来转移？是的，他们都与 \([l,r]\) 区间的左端点有交。

故我们再开一个数组 \(h_{i,j}\)，表示第 \(i\) 个区间经过 \(j\) 的方案数。\(h_{i-1,l}\to f_{i,l}\) 就行啦（这也是为什么刚刚使用小于号的原因）。

注意我们现在只列出了暴力转移的方程，推推式子前缀和优化就行了。

\[\begin{aligned} f_{i,l} & = \sum_{r=l}^{n} h_{i-1,l}+f_{i-1,l<l'\leq r} \\ & = (n-l+1)h_{i-1,l}+\sum_{r=l}^{n}Sf_{i-1,r}-Sf{i-1,l} \\ & = (n-l+1)h_{i-1,l}+\sum_{r=l}^{n}Sf_{i-1,r}-(n-l+1)Sf_{i-1,l} \end{aligned} \]

\[\begin{aligned} g_{i,r}&=\sum_{l=1}^{r}h_{i-1,r}+g_{i-1,l\leq r' < r} \\ & = r\times h_{i-1,r} + \sum_{l=1}^{r} Sg_{i-1,r-1}-Sg_{i-1,l-1} \\ & = r\times h_{i-1,r} + r \times Sg_{i-1,r-1} - \sum_{l=1}^{r} Sg_{i-1,l-1} \end{aligned} \]

\[tot=\sum_{l=1}^n f_{i,l} \\ \begin{aligned} h_{i,j}=tot-\sum_{r<j}g_{i,r}-\sum_{l>j}f_{i,l} \end{aligned} \]

\(S_f,S_g\) 表示一次前缀和，还要用二次前缀和优化。

#include <bits/stdc++.h>

using namespace std;

int P;
inline int Add(int x , int y){return x + y < P ? x + y : x + y - P;}
inline int Sub(int x , int y){return x < y ? x + P - y : x - y;}
inline int Mul(int x , int y){return 1LL * x * y % P;}

using IO_t=int;inline char gc(){static char buf[100000],*p1=buf,*p2=buf;return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;}inline IO_t read(){IO_t x=0;bool f=0;char ch=gc();while(!isdigit(ch)){f|=(ch=='-');ch=gc();}while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=gc();}return(f?-x:x);}

int n , m;

signed main(){
//	freopen("a.in" , "r" , stdin);
//	freopen("a.out" , "w" , stdout);
	
	n = read() , m = read() , P = read();
	
	int f[n + 1][m + 1] , g[n + 1][m + 1] , h[n + 1][m + 1];
	int F[n + 1][m + 1] , G[n + 1][m + 1];
	memset(f , 0 , sizeof f);
	memset(g , 0 , sizeof g);
	memset(h , 0 , sizeof h);
	memset(F , 0 , sizeof F);
	memset(G , 0 , sizeof G);
	
	for(int l = 1; l <= m; ++ l){
		f[1][l] = m - l + 1;
	}
	for(int r = 1; r <= m; ++ r){
		g[1][r] = r;
	}
	for(int j = 1; j <= m; ++ j){
		h[1][j] = Mul(j , m - j + 1);
	}
	for(int j = 1; j <= m; ++ j){
		f[1][j] = Add(f[1][j] , f[1][j - 1]);
		g[1][j] = Add(g[1][j] , g[1][j - 1]);
	}
	int tot = f[1][m];
	for(int j = 1; j <= m; ++ j){
		int tmp1 = g[1][j - 1];
		int tmp2 = Sub(f[1][m] , f[1][j]);
		h[1][j] = Sub(Sub(tot , tmp1) , tmp2);
	}
	for(int j = 1; j <= m; ++ j){
		F[1][j] = Add(f[1][j] , F[1][j - 1]);
		G[1][j] = Add(g[1][j] , G[1][j - 1]);
	}
	
	for(int i = 2; i <= n; ++ i){//f，g用完后变为前缀和
		//F,G为前缀和的前缀和
		for(int l = 1; l <= m; ++ l){
			int tmp1 = Mul(m - l + 1 , h[i - 1][l]);
			int tmp2 = Sub(F[i - 1][m] , F[i - 1][l - 1]);
			int tmp3 = Mul(m - l + 1 , f[i - 1][l]);
			f[i][l] = Add(tmp1 , Sub(tmp2 , tmp3));
		}
		for(int r = 1; r <= m; ++ r){
			int tmp1 = Mul(r , h[i - 1][r]);
			int tmp2 = Mul(r , g[i - 1][r - 1]);
			int tmp3 = Sub(G[i - 1][r - 1] , G[i - 1][0]);
			g[i][r] = Add(tmp1 , Sub(tmp2 , tmp3));
		}
		for(int j = 1; j <= m; ++ j){
			f[i][j] = Add(f[i][j] , f[i][j - 1]);
			g[i][j] = Add(g[i][j] , g[i][j - 1]);
		}
		int tot = f[i][m];
		for(int j = 1; j <= m; ++ j){
			int tmp1 = g[i][j - 1];
			int tmp2 = Sub(f[i][m] , f[i][j]);
			h[i][j] = Sub(Sub(tot , tmp1) , tmp2);
		}
		for(int j = 1; j <= m; ++ j){
			F[i][j] = Add(f[i][j] , F[i][j - 1]);
			G[i][j] = Add(g[i][j] , G[i][j - 1]);
		}
	}
	
//	assert(f[n][m] == g[n][m]);
	printf("%d" , g[n][m]);
	
	return 0;
}