CF1946D Birthday Gift 题解

看到位运算，我们可以按位考虑，毕竟 ^ | & 都不进位（以下的“位”均为二进制下的）

对 \(x\) ，我们从高位向低位考虑。由于 \(2\) 的幂的性质，高位若“胜负已分”，则低位不会对相对大小关系产生影响，这么做是可行的。

现在我们的复杂度添上了一层 \(log\)。

接着考虑，由于或 | 运算的性质，对于所有数的某一位来说，一旦出现了一个 \(1\) ，那么或之和中这一位必定为 \(1\) 。

由此，我们进行分类讨论。

1.若 \(x\) 的这一位是 \(1\) ，那么不等式左侧部分值的这一位可 \(0\) 可 \(1\)。

2.若 \(x\) 的这一位是 \(0\) ，那么不等式左侧部分值的这一位只能是 \(0\)，若有 \(1\) ，则我们不得不用异或的性质将 \(1\) 消去

那么如何将 \(1\) 消去呢？

从第一个该位为 \(1\) 的数开始考虑，由于我们不能打乱序列的顺序，所以第一个这样的数只能和第二个这样的的数抵消，第三个数不得不和第四个进行抵消

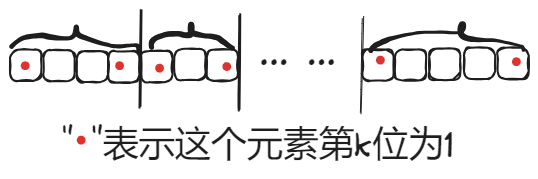
上图大括号内进行异或，竖直分割线表示相邻两个异或和之间或

注意，上述操作都是不得不这样做的，所以如果进行不下去，那么就说明无解TAT

需要注意的是：分类讨论的第一种情况的"可 \(0\) "情况之后就没必要进行下去了，因为后面要进行更多的合并，答案一定不优于现有的

具体到代码实现上来说，一个大括号内的异或和可以存到大括号开头的位置上，其余位置打上 \(-1\) 的标记，下次遍历到直接不管。

点击查看代码

#include <bits/stdc++.h>

using namespace std;

#define mkp make_pair
typedef unsigned long long ull;
typedef long long ll;

const int N = 1e5 + 5;
constexpr int INF = 0x3F3F3F3F;
constexpr ll INFl = 0x3F3F3F3F3F3F3F3F;
constexpr int P = 1e9 + 7;

#define typ int
#define writesp(x) write(x) , putchar(32)
#define writeln(x) write(x) , putchar(10)
inline char gc() {
	static char buf[100000] , *p1 = buf , *p2 = buf;
	return p1 == p2 && (p2 = (p1 = buf) + fread(buf , 1 , 100000 , stdin) , p1 == p2) ? EOF : *p1 ++ ;
}
#define getc gc // ------>>>REMEMBER<<<------
inline typ read(){
	typ x = 0; bool f = 0;
	char ch = getc();
	while(!isdigit(ch)){
		f |= (ch == '-');
		ch = getc();
	}
	while(isdigit(ch)){
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getc();
	}
	return (f ? -x : x);
}
inline void write(typ x){
	if(x < 0) putchar('-') , x = -x;
	if(x / 10) write(x / 10);
	putchar(x % 10 ^ 48);
}

int n , x , a[N] , b[N];
void solve(){
	int ans = -1 , Flg = 1;
	n = read() , x = read();
	for(int i = 1; i <= n; ++ i){
		a[i] = read();
	}
	for(int i = 30; i >= 0 && Flg; -- i){
		if((x & (1 << i))){
			int flg = 1;
			for(int j = 1; j <= n && flg; ++ j){
				if((a[j] & (1 << i)) != 0){
					flg = 0;
				}
			}
			if(flg == 1){
				int cnt = 0;
				for(int j = 1; j <= n; ++ j){
					cnt += (a[j] != -1);
				}
				ans = max(ans , cnt);
				break;
			}
			for(int i = 1; i <= n; ++ i) b[i] = a[i];
			int fflg = 1;
			for(int j = 1; j <= n; ++ j){
				if((b[j] & (1 << i)) == 0 || b[j] == -1){
					
				}
				else {
					int pos = j ++ ;
					while(j <= n && ((b[j] & (1 << i)) == 0 || b[j] == -1)){
						if(b[j] != -1) b[pos] ^= b[j] , b[j] = -1;
						++ j;
					}
					if(j > n){
						fflg = 0;
						break;
					}
					b[pos] ^= b[j];
					b[j] = -1;
				}
			}
			if(fflg == 1){
				int cnt = 0;
				for(int j = 1; j <= n; ++ j){
					cnt += (b[j] != -1);
				}
				ans = max(ans , cnt);
			}
		}
		else {
			
			for(int j = 1; j <= n; ++ j){
				if((a[j] & (1 << i)) == 0 || a[j] == -1){
					
				}
				else {
					int pos = j ++ ;
					while(j <= n && ((a[j] & (1 << i)) == 0 || a[j] == -1)){
						if(a[j] != -1) a[pos] ^= a[j] , a[j] = -1;
						++ j;
					}
					if(j > n){
						Flg = 0;
						break;
					}
					a[pos] ^= a[j];
					a[j] = -1;
				}
			}
		}
	}
	int orsum = 0 , cnt = 0;
	for(int i = 1; i <= n; ++ i){
		if(a[i] != -1){
			orsum |= a[i];
			++ cnt;
		}
	}
	if(orsum <= x) ans = max(ans , cnt);
	writeln(ans);
}

signed main(){
	int T = read();
	while(T -- ) solve();
	
	return 0;
}