LeetCode39. 组合总和

LeetCode39. 组合总和

题目叙述：

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合。

示例 1：

• 输入：candidates = [2,3,6,7], target = 7,
• 所求解集为： [ [7], [2,2,3] ]

示例 2：

• 输入：candidates = [2,3,5], target = 8,
• 所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

思路：

• 题目中提到同一个数字可以无限制的被选取，那么我们就想，如果这个数组中有0怎么办？那不是无穷选了？但是我们看到题目中说，所有数字都是正整数，所以我们放心了，我们可以先画出递归搜索树来形象的观察我们这题的操作过程

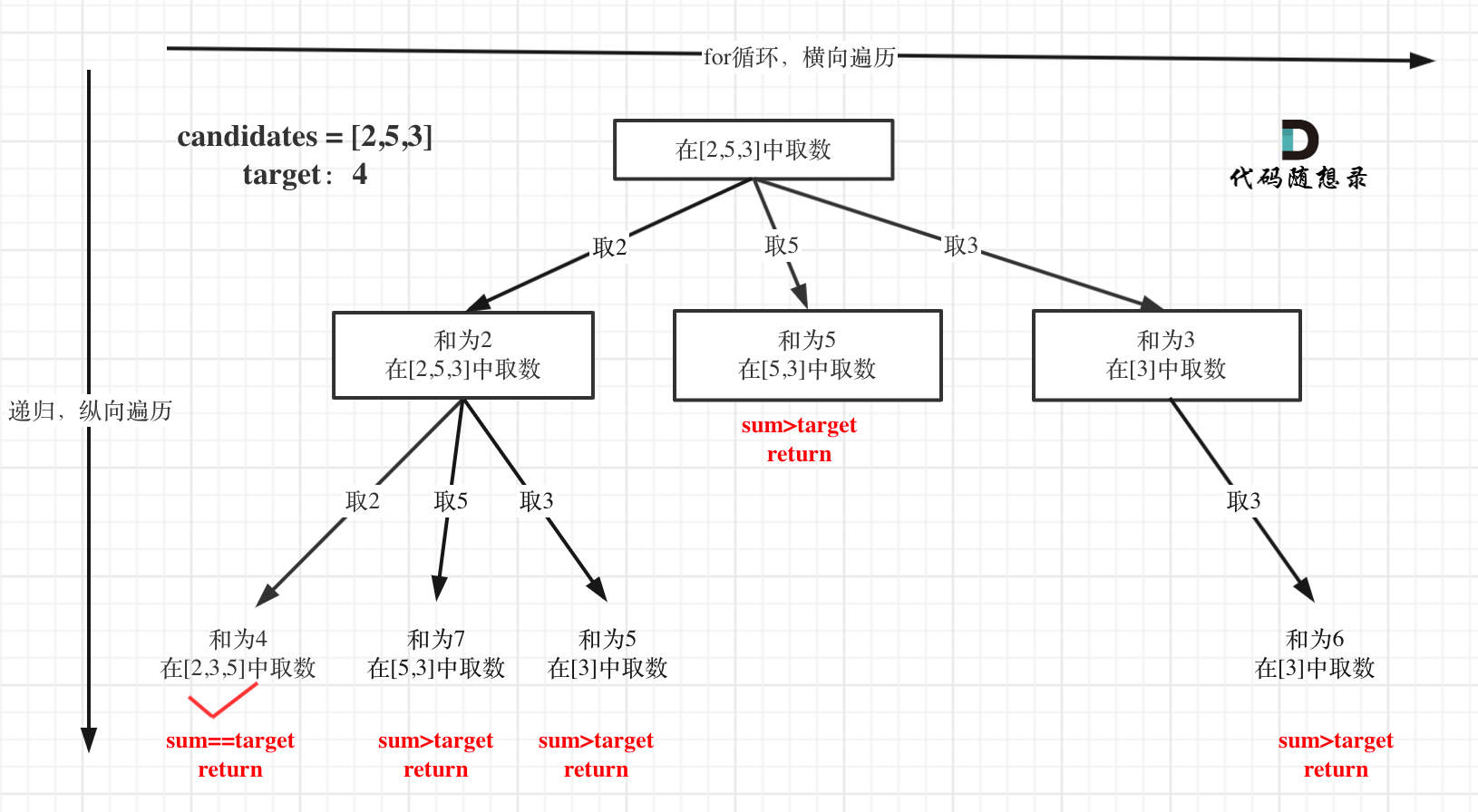
• 注：本图应用了代码随想录的原图，想要了解更加深刻的读者可以去看看原作者的文章：
• [代码随想录 (programmercarl.com)]()

1.回溯函数的参数以及返回值

• 我们需要一个一维数组path存放当前路径上的所有元素，并且需要一个二维数组result存放所有的结果。
• 需要传入一个目标值targetSum，这就是我们的目标和
• 并且我们需要一个sum来记录当前路径所有元素的总和，其实这个也不是必须的，我们可以通过加减targetSum来实现。不过这里我们介绍使用sum的方法，这样更加直观！

2.递归的中止条件

• 注意图中叶子节点的返回条件，因为本题没有组合数量要求，仅仅是总和的限制，所以递归没有层数的限制，只要选取的元素总和超过target，就返回！

//当sum≥targetSum就可以返回了
if(sum>=targetSum){
    if(sum==targetSum) result.push_back(path);
    return;
}

3. 单层递归的逻辑

• 我们通过for循环来控制横向遍历，通过控制递归函数来实现纵向遍历，不过这里的纵向遍历可就不是i+1了，而是i，这里一定要想清楚，因为这道题说一个元素是可以重复选取的！！！所以说纵向遍历的时候，是可以包括当前遍历的元素的，在代码体现上也就是递归函数的参数startindex==i，而不是i+1。

• 明白了这个之后，我们不难写出代码：

        for(int i=startindex;i<candidates.size();i++){
            sum+=candidates[i];
            path.push_back(candidates[i]);
            //这里是i，并不是i+1，因为同一个元素可以重复取
            backtracking(candidates,targetSum,sum,i);
            sum-=candidates[i];
            path.pop_back();
        }

• 在这里我们也可以隐藏回溯的过程，代码更简洁，但是初学者不推荐这种写法

        for(int i=startindex;i<candidates.size();i++){
            path.push_back(candidates[i]);
            //将回溯过程隐藏在递归函数当中
            backtracking(candidates,targetSum,sum+candidates[i],i);
            path.pop_back();
        }

代码：

• 通过上面的分析，我们不难得出代码：

class Solution {
public:
    vector<int> path;
    vector<vector<int> > result;
    void backtracking(vector<int> candidates,int targetSum,int sum,int startindex){
        if(sum>=targetSum){
            if(sum==targetSum) result.push_back(path);
            return;
        }
        for(int i=startindex;i<candidates.size();i++){
            //使用sum加减更直观，也可以隐藏到回溯函数当中。
            sum+=candidates[i];
            path.push_back(candidates[i]);
            //这里是i，并不是i+1，因为同一个元素可以重复取
            backtracking(candidates,targetSum,sum,i);
            sum-=candidates[i];
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        path.clear();result.clear();
        if(candidates.size()==0) return result;
        backtracking(candidates,target,0,0);
        return result;
    }
};