4.26 前缀和/差分数组（处理区间问题）

1 前缀和（第一行/第一行+第一列变成0）
1.1元素和
一维：利用数列的技巧：Sn-Sm=A_{m_1}+……+A_{n}
1.2 二维矩阵
任意一个矩阵之和可以转化成几个大矩阵（左上角都是0，0）的线性运算

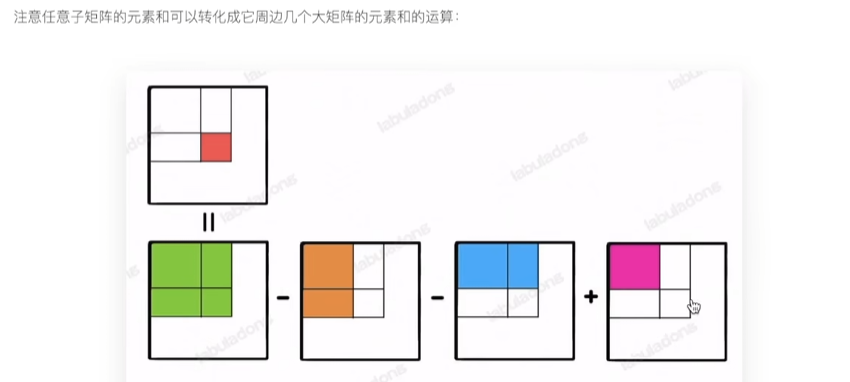
前缀和（积）的使用条件：
1.原数组不变，如果原数组某一个值发生变化，那么presum的值也会变化
2.存在逆运算，比如x+8=10,x*6=12都可以求出来x的值，但是max(x,8)就求不出来x的值

核心算法：
class PrefixSum {
// 前缀和数组
private int[] preSum;

// 输入一个数组，构造前缀和
public PrefixSum(int[] nums) {
    // preSum[0] = 0，便于计算累加和
    preSum = new int[nums.length + 1];
    // 计算 nums 的累加和
    for (int i = 1; i < preSum.length; i++) {
        preSum[i] = preSum[i - 1] + nums[i - 1];
    }
}

// 查询闭区间 [left, right] 的累加和
public int sumRange(int left, int right) {
    return preSum[right + 1] - preSum[left];
}

}

2 差分数组（频繁修改原始数组的某个区间里的元素）
差分数组的的哥元素是nums的第一个元素，（每一个元素是[i+1]-[i]）
diff数组可以让某一个区间同时增加/减少，只需要改两个数字就可以更改一个区间的值

总结：前缀和可以进行区间的快速查询，差分数组可以进行区间的快速增减
差分数组的问题：必须创建一个和区间同样大的数组

处理区间的进阶技巧--线段树