3.14 二重积分

1
1.1
概念引入


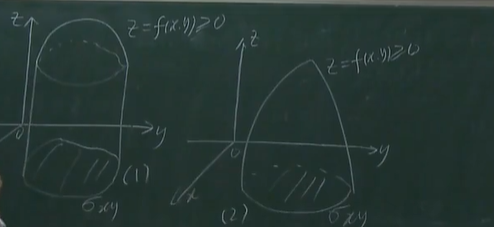
1.2 分、匀、和、均
分割：把XOY平面分割成若干个小区域，相应的，把柱体分割成n个小的曲顶柱体
取近似：取某一小块的一个点，通过函数关系确定此点的高，体积就等于此处的·面积*高
作和：把每一小块的体积加起来，作为曲顶柱体的体积
取极限：设λ，λ趋近于0，使每一个体积趋近于最小，即可求出曲顶柱体的体积


1.3 二重积分的定义

后续推导，二重积分可以化成两次一元积分

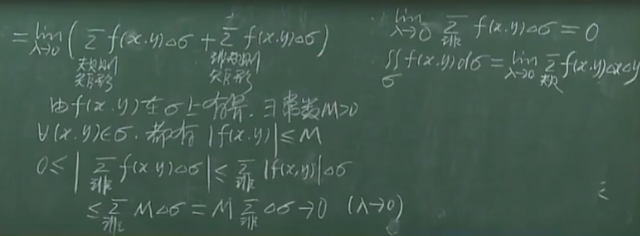
最终可以化成dxdy
1.4 二重积分的性质（大部分性质和普通积分差不多）

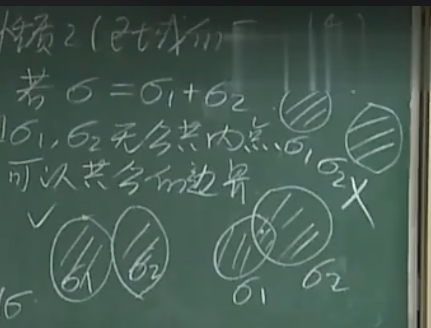
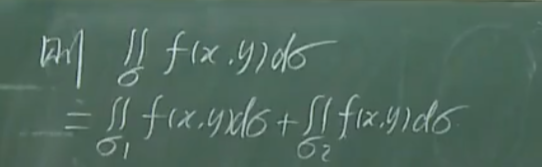
2.二重积分的计算
2.1 X型区域（D的边界垂直于X轴，或者和垂直于X轴的直线只有一个交点）

然后把图形分成 上曲线和下曲线
先积分y，再积分x
同样的，还有y型区域
2.2 二重积分化成累次积分的运算
以x型积分为例子（一元积分辅助理解）
取二重积分的一个切面➡可近似看成是一元积分

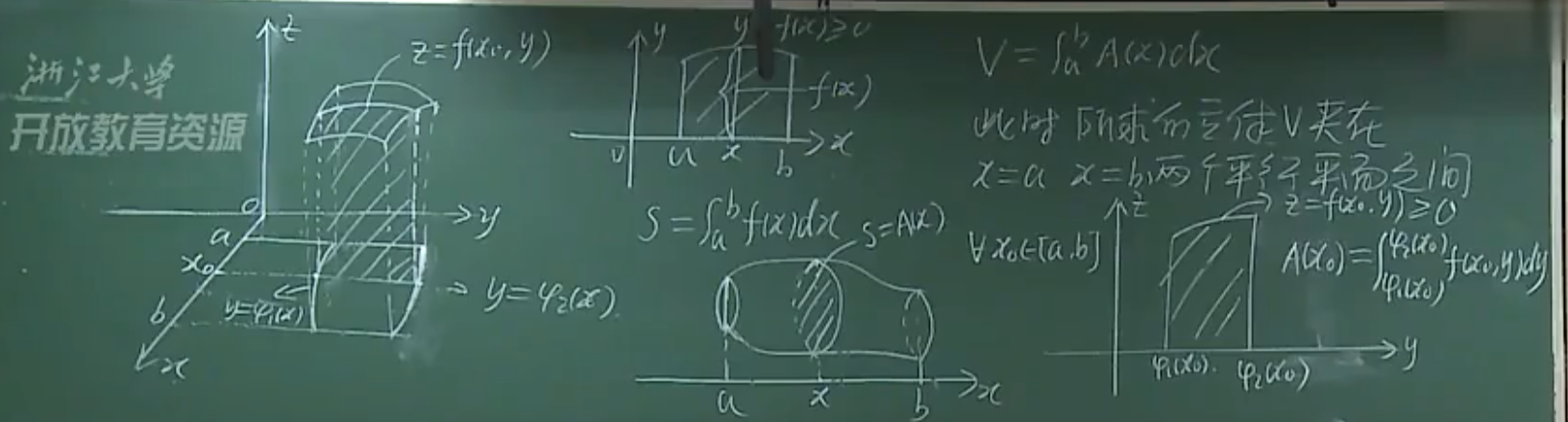
先积分y()x=x0，再积分x

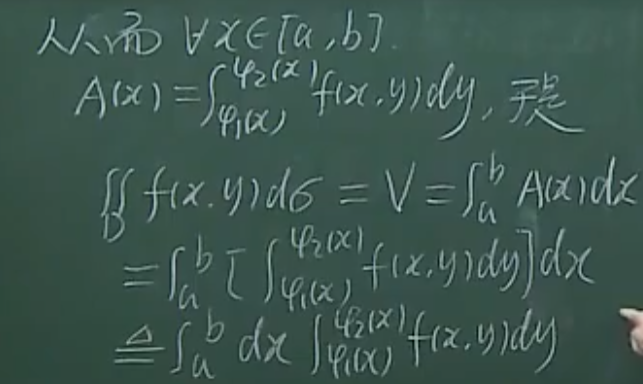
如果不是x/y型区域，可以增加辅助线，分成几个小区域，化成x/y型区域
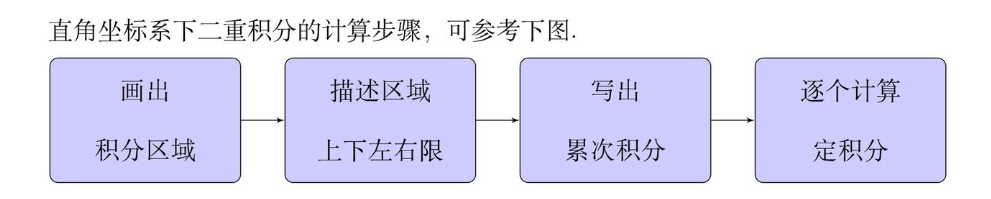
总结：计算二重积分的步骤
1.画出积分区域D
（i）如果D的区域为两条曲线，先求出交点，画经过交点的边界曲线
（ii）如果D的边界超过两条曲线，在画边界曲线的过程中，求出交点，画出区域
2.若D为X型区域，则二重积分先积分y，再积分x
等等

例题(欸，我例题呢？)

知乎上的讲解（如何解释二重积分）

极坐标系下的二重积分

最终解题路径

轮换对称：关于y=x对称
总结：