「Day 2—贪心问题&分治&前缀和」

贪心问题

定义

顾名思义，越贪越好。。。

习题

P1094 [NOIP2007 普及组] 纪念品分组

思路

简单来说：最少的+最多的，利用双指针。

代码

#include<algorithm>
#include<iostream>
using namespace std;

int w,n;
int p[30005];

int main(){
    cin>>w;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>p[i];
    }
    sort(p+1,p+n+1);
    int l=1,r=n,ans=0;
    while(l<=r){
        if(p[l]+p[r]<=w){
            l++;
            r--;
            ans++;
        }
        else{
            r--;
            ans++;
        }
    }
    cout<<ans<<"\n";
    return 0;
}

P1803 凌乱的yyy / 线段覆盖

思路

按照右端点进行排序，每次选择右端点，判断当前的右端点是否比下一个的左端点小，如果小，证明其需要更新。

代码

#include<iostream>
#include<algorithm>
using namespace std;

struct node{
    int x,y;
}p[1000005];
int n;
bool cmp(node x,node y){
    return x.y<y.y;
}

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>p[i].x>>p[i].y;
    }
    sort(p+1,p+n+1,cmp);
    int id=0,ans=0;
    for(int i=1;i<=n;i++){
        if(id<=p[i].x){
            id=p[i].y;
            ans++;
        }
    }
    cout<<ans<<"\n";
    return 0;
}

P1181 数列分段 Section I

思路

每次从前向后加，如果大于 \(m\)，则更新为当前值，否则就加上。

代码

#include<iostream>
using namespace std;

int n,a[100005];
int ans=0,m,cnt=0;

int main(){

    cin>>n>>m;

    for(int i=1;i<=n;i++){
        cin>>a[i];
        if(cnt+a[i]>m){
            ans++;
            cnt=a[i];
        }
        else cnt+=a[i];
    }
    cout<<++ans<<"\n";
    return 0;
}

UVA1615高速公路 Highway & P1325 雷达安装

思路

这两题几乎一样，除了一些小差别，那么，怎么做呢。我们相当于以 \(x\) 正半轴上一点，做半径为 \(D\) 的圆，使其覆盖到的点尽可能多，但是，这样明显不太行。我们换种思路，以所有村庄为圆心，做半径为 \(D\) 的圆，交 \(x\) 的正半轴为 \(l，r\)，则我们选的点在这个区间内即可覆盖到此点，于是乎，这个题就变成了我们熟悉的线段覆盖。，那么问题又来了， \(l，r\) 如何计算呢，我采用了勾股定理进行计算，十分简单。

代码

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;

double oj(int x,int y){
    return sqrt((x - y) * (x - y));
}

struct node{
    int x,y;
    double lx,ly;
}v[100005];
int L,n,D;

bool cmp(node x,node y){
	if(x.ly == y.ly){
		return x.lx < y.lx;
	}
	return x.ly < y.ly;
}


int main(){
    while(scanf("%d %d %d",&L,&D,&n)!=EOF){
    	for(int i = 1;i <= n;i++){
	        cin >> v[i].x >> v[i].y;
	        v[i].lx = v[i].x - sqrt(D * D - v[i].y * v[i].y);
	        v[i].ly = v[i].x + sqrt(D * D - v[i].y * v[i].y);
	    }
		sort(v + 1,v + n + 1,cmp);
		int ans = 0;
		int id = -114514;
		for(int i = 1;i <= n;i++){
			if(v[i].lx > id){
				ans++;
				id = v[i].ly;
			}
		}
		cout << ans <<"\n";
	}
    return 0;
}

分治

定义

分治的思路就是将一个大问题平分为两个小问题，再继续平分，直到问题的规模小到可以直接解决，解决后，再通过递归，将其每两个小问题合并，最后完成。

习题

P1908 逆序对

思路

这个题，首先暴力是肯定不对的，因为 \(n\) 的范围在 \(5*10^5\) 左右，所以我们要考虑一些简单的写法，于是，我们可以利用归并排序的基本原理，即 \(a[i]>a[j]\)，交换。所以我们在交换时将答案记录加上 \(mid-i+1\)（\(ans\) 直接++是不对的），原因是一旦左半边 \(a[i]>a[j]\)，而又因为其两边都是有序的，故从 \(i~mid\) 全大于右面的，则 \(ans+=mid-i+1\)。
而归并排序的流程如下：

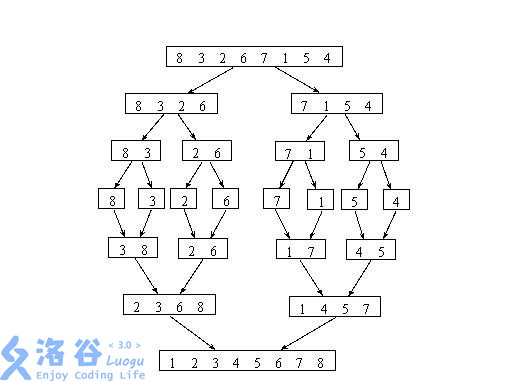
注：归并排序的时间复杂度是 \(O(n log n)\)

代码

#include<iostream>
using namespace std;

#define ll long long
const int MAXN=5*1e5+5;

ll n;
ll a[MAXN];
ll tmp[MAXN];
ll ans = 0;

void qsort(ll l,ll r){
	if(l == r){
		return;
	}
	ll mid = (l + r) / 2;
	ll i = l,j = mid + 1;
	ll k = l; 
	qsort(l,mid);
	qsort(mid + 1,r);
	while(i <= mid && j <= r){
		if(a[i] <= a[j]){
			tmp[k++] = a[i++];
		}
		else{
			tmp[k++] = a[j++];
			ans += mid - i + 1;
		}
	}
	while(i <= mid){
		tmp[k++] = a[i++];
	}
	while(j <= r){
		tmp[k++] = a[j++];
	} 
	for(int v = l;v <= r;v++){
		a[v] = tmp[v];
	}
}

int main(){
	cin>>n;
	for(int i = 1;i <= n;i++){
		cin >> a[i];
	}
	qsort(1,n);
	cout << ans <<"\n";
	return 0;
}

P1824 进击的奶牛

思路

这个题吧，就很明显，让最小值最大或者最大值最小的题，一般来说都是二分，而这道题明显的是一个二分答案，每次枚举这个隔间距离，看是否满足。

代码

#include<iostream>
#include<algorithm>
using namespace std;

int n,m,ans=0;
int x[100005];

bool check(int dis){
	int sum = 1;
	int id = x[1];
	for(int i = 2;i <= n;i++){
		if(x[i] - id >= dis){
			sum++;
			id = x[i];
		}
	}
	return (sum >= m);
} 

int main(){
	cin >> n >> m;
	
	for(int i = 1;i <= n ;i++){
		cin >> x[i];
	}
	sort(x + 1,x + n + 1);
	int l = 1,r = 1e9;
	while(l <= r){
		int mid = (l & r) + ((l ^ r) >> 1);
		if(check(mid)){
			ans = mid;
			l = mid + 1;
		}
		else{
			r = mid - 1;
		}
	}
	cout << ans <<"\n";
	return 0;
}

前缀和

定义

利用前缀数组快速计算区间和的方法。

习题

P2878 [USACO07JAN] Protecting the Flowers S

思路

贪心+排序+前缀和优化，按每分钟吃花的多少排序，吃的多的先牵回来。

代码

#include<iostream>
#include<algorithm>
using namespace std;

#define int long long

struct node{
	int t,d;
	double cnt;
}c[2000005];
int n,ans=0;
int sum[2000005];

bool cmp(node x,node y){
	return x.cnt > y.cnt;
}

signed main(){
	cin >> n;
	for(int i = 1;i <= n;i ++){
		cin >> c[i].t >> c[i].d;
		c[i].cnt = double(c[i].d * 1.00 / c[i].t * 1.00);
	}
	sort(c + 1,c + n + 1,cmp);
	for(int i = 1;i <= n;i ++){
		sum[i] = sum[i - 1] + c[i].d;
	}
	for(int i = 1;i <= n;i ++){
//		ans = ans + c[i].d * c[i].t;这一行千万不要加，题目没说，坑死了
		ans = ans + (sum[n] - sum[i]) * (2 * c[i].t);
	}
	cout << ans << "\n";
	return 0;
}