「Day 1—递归问题」

合集 - C++信息竞赛(17)

1.CSP考前2023-10-04

2.「Day 1—递归问题」2024-08-04

3.「Day 2—贪心问题&分治&前缀和」2024-08-054.「Day 3—深度优先搜索 & 广度优先搜索」2024-08-065.「Day 4—图的存储 & 图上搜索」2024-08-116.「Day 5—最短路径」2024-08-117.「Day 6—单调栈 & 单调队列 & 并查集」2024-08-118.「Day 7—离散化 & 树状数组 & 线段树」2024-08-129.「Day 8—最小生成树之Kruskal & Prim」2024-08-1210.「Day 9 & 10—DP问题」2024-08-1411.「Day 11 & 12 & 13 & 14—杂项」2024-08-1712.「2024 - 暑假 - Day-1 提高笔记-割点(割边)」2024-10-0913.「2024 - 暑假 - Day-2 提高笔记-字典树」2024-10-1614.【基础知识】2024-10-1815.「2024 - 暑假 - Day-3 提高笔记-ST表 & RMQ」2024-10-2216.「2024 - 暑假 - Day-4 提高笔记-LCA最近公共祖先」2024-10-2217.「2025 - 寒假 - Day-2 提高笔记-反悔贪心」01-22

收起

递归问题

定义

简洁来说就是一个函数不断调用自身的一个过程。

习题

汉诺塔问题

思路

对于这个经典的问题，我们考虑了使用递归的做法，由于盘子是在三个底座上来回辗转的，所以我们要确定起始座，辅助座，和目标座。我们专注于最下面的最大的那个盘子，先将盘子都放到辅助座上，等到只剩最大的，将其放到目标座上，再继续由辅助座向目标座转移。

代码

void hanoi(int n,char a,char b,char c){
	if(n > 0){
		hanoi(n - 1,a,c,b);
		cout<<a<<"->"<<n<<"->"<<b;
		hanoi(n - 1,b,a,c);
	}
	return;
}

P5657 [CSP-S2019] 格雷码

思路

首先我们在读题的过程中就可以观察到，对于 $n$ 位的格雷码，必须由 $n-1$ 推出来，我们不免想到通过递归来实现，但在仔细观察之后会发现：

以 $3$ 位格雷码为例，分别是 000，001，011，010，110，111，101，100；那么他们是怎么得出来的呢，观察下图：

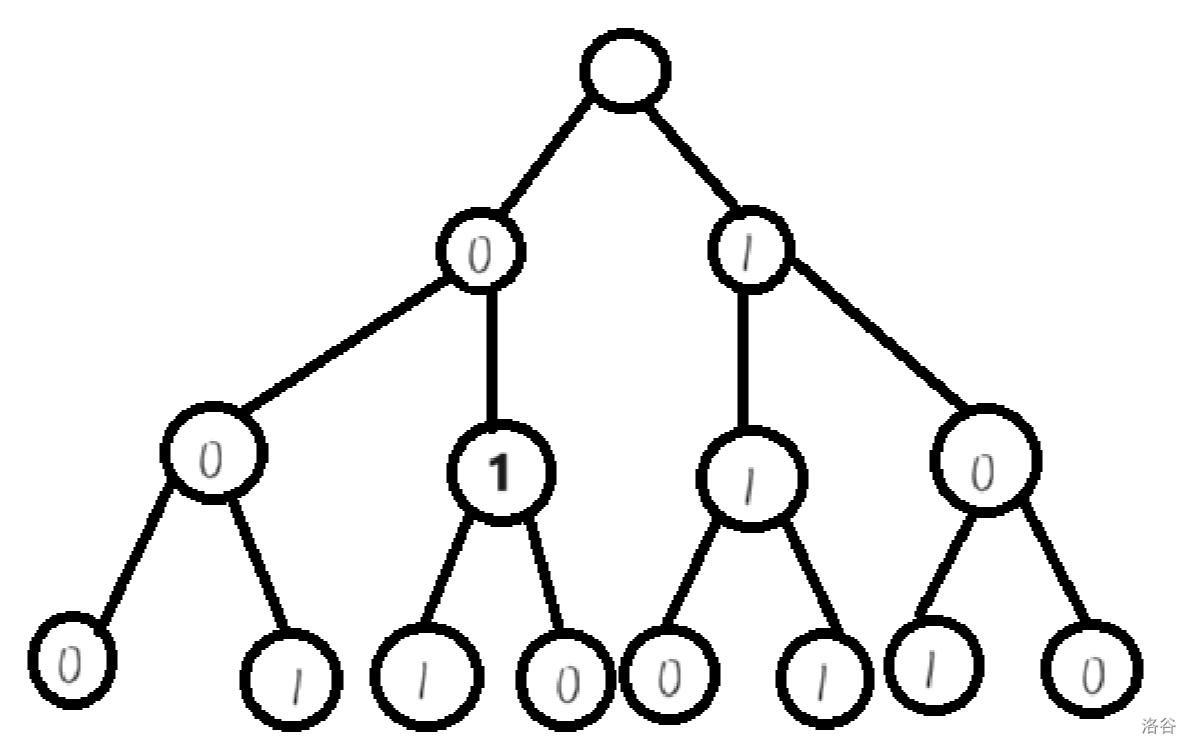
我们发现格雷码是有规律的，分为前一半和后一半，前为 $0$，后为 $1$，比较像一个二叉树，因为后面一半是逆序，所以左右对称。在左半边，所以如果根为 $0$，那么左子树为 $0$，右子树为 $1$；如果根为 $1$，那么左子树为 $1$，右子树为 $0$。右半边则相反.

代码

#include<iostream>
#include<cmath>
using namespace std;

unsigned long long n,k;
bool flag = 0;

int main(){
	cin >> n >> k;
	unsigned long long mid = pow(2,n-1);
	while(mid){
		if(!flag){
			if(k < mid){
				cout << "0";
				flag = 0;
			}
			else if(k >= mid){
				cout << "1";
				flag = 1;
				k = k - mid;
			}
		}
		else if(flag){
			if(k < mid){
				cout << "1";
				flag = 0;
			}
			else if(k >= mid){
				cout << "0";
				flag = 1;
				k = k - mid;
			}
		}
		mid /= 2;
	}
	return 0;
}

UVA679 Dropping Balls

思路

对于此题，我们依旧按朴素的思路，将 $I$ 之前全模拟一遍，但是，我们发现，会 $TLE$。故我们进行一些优化，根为n，则左子树为 $2\ast n$，右子树为 $2\ast n+1$，接下来我们需要看第 $I$ 个小球会走哪里，通过观察发现，当 $I$ 为偶数时，先走左边，反之。

代码

#include<iostream>
using namespace std;

int T;

int main(){
	
	cin >> T;
	
	while(T--){
		int deep,id,ans = 1;
		cin >> deep >> id;
		for(int i = 1;i < deep;i++){
			if(id % 2 == 1){
				ans = ans * 2;
				id = id / 2 + 1;
			}
			else{
				ans = ans * 2 + 1;
				id = id / 2;
			}
		}
		cout << ans <<"\n";
	}
	
	
	return 0;
}