zkw 线段树-原理及其扩展
前言
许多算法的本质是统计。线段树用于统计,是沟通原数组与前缀和的桥梁。
《统计的力量》清华大学-张昆玮
关于线段树
前置知识:线段树 OIWiki。
线段树是一种专门维护区间问题的数据结构。
线段树对信息进行二进制化处理并在树形结构上维护,以此让处理速度达到 \(O(\log{n})\) 级别。
线段树的实现方式
由于线段树的树形结构特点,每次修改查询可以从根节点向下二分查找需要用到的节点,因此较为普遍且快捷的线段树会使用递归实现。
但递归实现的线段树由于每次要从根节点递归向下传递子树信息,导致常数较大,容易被卡常,所以出现了常数更小的递推实现的线段树(膜拜 zkw 大佬)。
zkw 线段树
先来讲一些小原理。
一、原理
由于递归实现的线段树不是一棵满二叉树,其叶子节点位置不确定,导致每次操作都需要从根节点开始自上而下递归依次寻找叶子节点,回溯时进行维护,递归过程常数就比较大了。
所以 zkw 线段树就直接建出一棵满二叉树,原序列信息都维护在最底层。严格规定父子节点关系,同层节点的子树大小相等。
这样每个叶子节点都可以直接找到并修改,由于二叉树父子节点的二进制关系,就可以递推直接找到对应节点的父亲节点自下而上地维护节点关系。
二、初始化
1、建树
对长度为 \(n\) 的序列建一棵 zkw 线段树,其至少有 \(n+2\) 个叶子节点。其中有 2 个用来帮助维护区间信息的虚点,有 \(n\) 个用来存原序列信息的节点。
如图(【模板】线段树 1 的样例为例,下同):
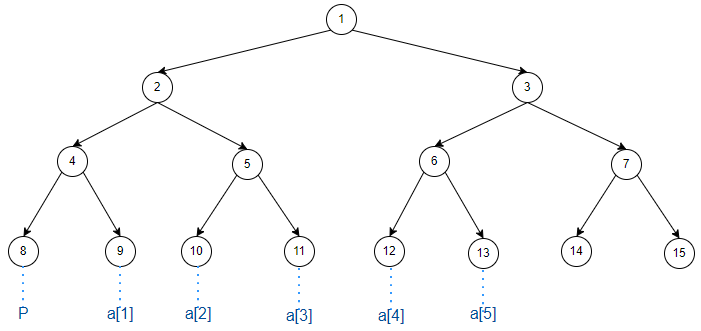
建树时先求出虚点 \(P\) 位置,然后直接向其他叶子节点读入信息即可:
//先求虚点 P
P = 1;
while(P<=n+1) P<<=1;//节点深度每增加一层,当前层节点数量扩大一倍
for(int i=1;i<=n;++i) read(tr[P+i]);
2、维护
根据上文所说,由于严格确定了父子关系,所以直接自下而上遍历所有节点维护父子关系做初始化:
//push_up
for(int i=P-1;i;--i){//i=(P+n)>>1
tr[i] = tr[i<<1|1]+tr[i<<1];
tr[i] = min(tr[i<<1|1],tr[i<<1]);
tr[i] = max(tr[i<<1|1],tr[i<<1]);
//...
}
三、概念介绍
1、永久化懒标记
与递归线段树的 \(lazy\) \(tag\) 不同,其每次向下递归时都需要先下放标记并清空以维护信息。
但在维护存在结合律的运算时,zkw 线段树的 \(lazy\) \(tag\) 只会累加,而不会在修改和查询前下放清空。
2、“哨兵”节点
在区间操作时,引入两个哨兵节点,分别在区间的左右两侧,把闭区间变成开区间进行处理。
两个哨兵节点到根有两条链,与两条链相邻且在中间部分的节点,就是这次操作需要用到其信息的所有节点。
如图(沿用了第一个图,节点中的数的为节点编号):
例如:【模板】线段树 1 第一个操作 \(query(2,4)\):
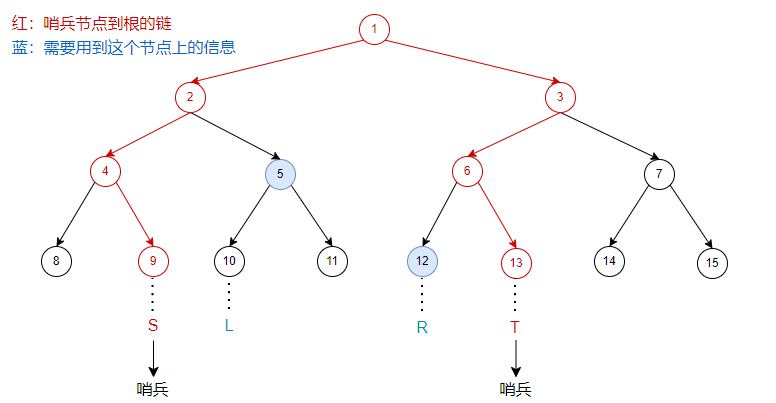
同时,这也解释了为什么建树时叶子节点上会有 \(2\) 个虚点。
(1)为什么可以确定需要用到哪些节点
操作时,只需要操作区间中单元素区间的公共祖先即可。
我们选取的两条链,中间部分正好包含了与操作区间有关的所有节点,与两条链相邻的节点显然的所有区间的公共祖先。
操作时只需要操作这些节点上的信息就可以了。
(2)在递推过程中怎么判断要用到哪些节点
观察我们刚才手推出来的图片,注意到:
对于左哨兵 \(S\),当它是左儿子时,其兄弟节点是需要用到的;
对于右哨兵 \(T\),当它是右儿子时,其兄弟节点是需要用到的。
每次操作完后 \(S\) 和 \(T\) 向上走到自己的父亲节点,然后维护父子关系,再进行新一轮操作。
当 \(S\) 和 \(T\) 互为兄弟节点时(走到了两条链的交点),就停止操作,然后向上维护信息到根节点。
四、基于结合律的查询与修改
1、区间修改
以区间加为例。
类似递归线段树操作,更新时需要知道当前节点的子树大小。
每次更新时,当前节点的值增加的是其标记乘子树大小;其标记的值正常累加即可。
永久化懒标记减少了标记下放带来的常数。
//
inline void update_add(int l,int r,ll k){
l=P+l-1; r=P+r+1;//哨兵位置
int siz = 1;//记录当前子树大小
while(l^1^r){//当l与r互为兄弟时,只有最后一位不同
if(~l&1) tr[l^1]+=siz*k,sum[l^1]+=k;
if(r&1) tr[r^1]+=siz*k,sum[r^1]+=k;
//类似递归线段树 tr[p] += tag[p]*(r-l+1)
l>>=1; r>>=1; siz<<=1;
//每次向上走时子树大小都会增加一倍
tr[l] = tr[l<<1]+tr[l<<1|1]+sum[l]*siz;//维护父子关系
tr[r] = tr[r<<1]+tr[r<<1|1]+sum[r]*siz;
}
for(l>>=1,siz<<=1;l;l>>=1,siz<<=1) tr[l] = tr[l<<1]+tr[l<<1|1]+sum[l]*siz;//更新上传至根节点
}
2、区间查询
由于我们需要查询的区间被左右哨兵分为了两个部分,但两部分子树大小不一定相等。
所以要分别维护左右哨兵到达的节点所包含查询区间的子树的大小。
//
inline ll query_sum(int l,int r){
l=l+P-1; r=r+P+1;
ll res = 0;
int sizl = 0,sizr = 0,siz = 1;//分别维护左右两侧子树大小
while(l^1^r){
if(~l&1) res+=tr[l^1],sizl+=siz;//更新答案及子树大小
if(r&1) res+=tr[r^1],sizr+=siz;
l>>=1; r>>=1; siz<<=1;
res += sum[l]*sizl+sum[r]*sizr;
//即使当前节点所存的区间和不需要用,但因为其是两个哨兵的父亲节点,且 tag 不会下传,
//所以其 tag 会对答案有贡献,所以需要加上 tag 的贡献
}
for(l>>=1,sizl+=sizr;l;l>>=1) res+=sum[l]*sizl;//累加至根节点
return res;
}
如果维护区间最大值也同理:
//
inline void update_add(int l,int r,ll k){
l=P+l-1; r=P+r+1;
while(l^1^r){
if(~l&1) sum[l^1]+=k,maxn[l^1]+=d;
if(r&1) sum[r^1]+=k,maxn[r^1]+=d;
l>>=1; r>>=1;
maxn[l] = max(maxn[l<<1],maxn[l<<1|1])+sum[l];
maxn[r] = max(maxn[r<<1],maxn[r<<1|1])+sum[r];
}
for(l>>=1;l;l>>=1) maxn[l]=max(maxn[l<<1],maxn[l<<1|1])+sum[l];//更新上传至根节点
}
inline ll query_max(int l,int r){
l=l+P-1; r=r+P+1;
ll resl = 0,resr = 0;//分别记录左右两侧最大值
while(l^1^r){
if(~l&1) resl=max(resl,maxn[l^1]);
if(r&1) resr=max(resr,maxn[r^1]);
l>>=1; r>>=1;
resl += sum[l];//标记永久化,所以要累加标记值
resr += sum[r];
}
for(resl=max(resl,resr),l>>=1;l;l>>=1) res1+=sum[l];//累加至根节点
return resl;
}
某些时候,只会用到单点修改区间查询和区间修改单点查询,此时 zkw 线段树码量优势很大。
3、单点修改下的区间查询
修改:直接改叶子结点的值然后向上维护。
查询:哨兵向上走时直接累加节点值。
//
inline update(int x,ll k){
x += P; tr[x] = k;
for(x>>=1; x ;x>>=1) tr[x] = tr[x<<1]+tr[x<<1|1];
}
inline ll query(int l,int r){
l += P-1; r += P+1;
ll res = 0;
while(l^1^r){
if(~l&1) res+=tr[l^1];
if(r&1) res+=tr[r^1];
l>>=1; r>>=1;
}
return res;
}
4、区间修改下的单点查询
将赋初值的过程看作是在叶子节点上打标记,区间修改也是在节点上打标记。
由于 zkw 线段树的标记是永久化的,所以此时将标记的值看作节点的真实值。
但这种做法显然只对于单点查询有效,在查询时需要加上节点到根沿途的所有标记。
//
inline void update_add(int l,int r,ll k){
l += P-1; r += P+1;
while(l^1^r){
if(~l&1) tr[l^1]+=k;
if(r&1) tr[r^1]+=k;
l>>=1; r>>=1;
}
}
inline ll query(int x){
ll res = 0;
for(x+=P; x ;x>>=1) res+=tr[x];
return res;
}
5、标记永久化的局限性
以上修改与查询方式,全部基于运算具有结合律,所以标记可以永久化,以此减少标记下放增加的常数。
但如果运算存在优先级,标记就不能再永久化了。考虑在更新时将先标记下放(类似递归线段树)然后再从叶子节点向上更新。
但是如果像递归线段树一样从根开始逐次寻找子节点下放一遍的话,那优化等于没有。
所以要考虑基于 zkw 线段树的特点进行下放操作,而且要尽可能的简洁方便。
So easy,搜一紫衣。
五、有运算优先级的修改与查询
1、标记去永久化
在进行区间修改时,我们会用到的节点只存在于哨兵节点到根的链上。
所以只考虑将这两条链上的节点标记进行下放即可。
(1)如何得到有哪些需要下放标记的节点
考虑最暴力的方法:
每次从哨兵节点向上递归直至根节点,回溯时下放标记。
显然这样的方式常数优化约等于零。
考虑优化肯定是基于 zkw 线段树的特点。
还是由于 zkw 线段树是满二叉树结构,所以可以通过节点编号移位的方式找到其所有父子节点的编号。
显然哨兵到根节点的链,是哨兵的所有父亲组成的,所以只要让哨兵编号移位就可以了。
(2)如何自上而下的传递标记
再记录一下叶子节点的深度。
思考满二叉树的性质:当节点编号右移位节点深度时就指向根节点编号。
所以节点右移的位数,从节点深度依次递减,就可以自上而下得到其所有父亲节点的编号。
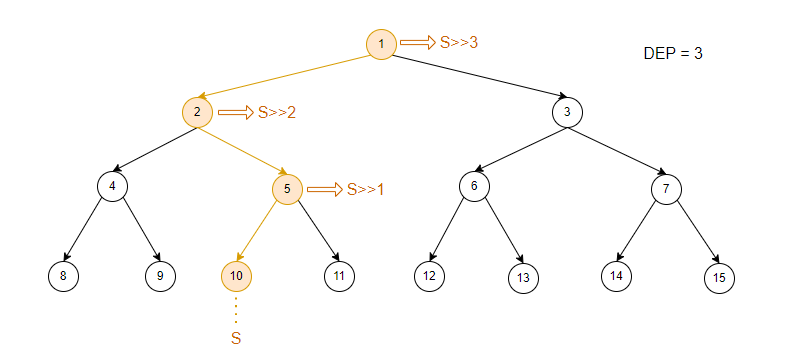
2、区间修改
先下放标记,然后正常做标记更新。
传递标记时可能要考虑子树大小,直接通过深度计算就可以了。
以区间加及乘为例:
//建树时记录叶子节点深度
P = 1;DEP = 0;
while(P<=n+1) P<<=1,++DEP;
//...
//...
//...
inline void update_add(int l,int r,ll k){
l=P+l-1; r=P+r+1;
//先下放标记
for(int i=DEP;i;--i) push_down(l>>i,1<<i),push_down(r>>i,1<<i);
//push_dwon( 链上节点 , 当前子树大小 );
int siz = 1;
while(l^1^r){
if(~l&1) tr[l^1]+=siz*k,sum[l^1]+=k;//正常更新
if(r&1) tr[r^1]+=siz*k,sum[r^1]+=k;
l>>=1; r>>=1; siz<<=1;
//维护父子关系
tr[l] = tr[l<<1]+tr[l<<1|1];//由于标记已下放,所以维护时不再考虑累加标记
tr[r] = tr[r<<1]+tr[r<<1|1];
}
for(l>>=1; l ;l>>=1) tr[l] = tr[l<<1]+tr[l<<1|1];//上传至根节点
}
//
inline void update_mul(int l,int r,ll k){
l += P-1; r += P+1;
for(int i=DEP;i;--i) push_down(l>>i,1<<i),push_down(r>>i,1<<i);
while(l^1^r){
if(~l&1) tr[l^1]*=k,mul[l^1]*=k,sum[l^1]*=k;//标记覆盖
if(r&1) tr[r^1]*=k,mul[r^1]*=k,sum[r^1]*=k;
l>>=1; r>>=1;
tr[l] = tr[l<<1]+tr[l<<1|1];
tr[r] = tr[r<<1]+tr[r<<1|1];
}
for(l>>=1; l ;l>>=1) tr[l] = tr[l<<1]+tr[l<<1|1];
}
3、区间查询
先下放标记。
由于标记已经去永久化,所以直接累加节点值即可。
//
inline ll query(int l,int r){
l = l+P-1;r = r+P+1;
//先下放标记
for(int i=DEP;i;--i) push_down(l>>i,1<<i),push_down(r>>i,1<<i);
ll res = 0;
while(l^1^r){
if(~l&1) res+=tr[l^1];
if(r&1) res+=tr[r^1];
//由于标记已下放,所以无需再累加标记的贡献
l>>=1; r>>=1;
}
return res;
}
六、优化效果
1、时间复杂度
开始的时候也提到了:递归线段树常数大的瓶颈在于其需要对树进行递归遍历以找到目标节点,然后回溯进行信息维护。
zkw 线段树仅仅只是优化了递归寻找目标节点这样的遍历过程的常数。
如果是追求常数或者注重优化遍历,那 zkw 线段树的优化就比较明显了;如果要维护较为复杂的信息,那么显然这点常数并不是很够看,此时就需要在其他地方上做改进了。
2、空间复杂度
zkw 线段树需要开三倍空间,普通线段树如果不使用动态开点需要开四倍空间。
相较于普通线段树,zkw 线段树代码好理解也比较简洁,不会出现忘建树和忘终止递归的问题,而且满二叉树结构的确定性让手造数据也比较方便。
对于一些维护信息复杂的题目,zkw 线段树的优势在于手推时思路更加清晰。
如果性格比较内向,不敢用递归线段树进行递归维护信息。
想用 zkw 递推实现更多更强的操作怎么办!
zkw 线段树实现其他线段树结构
一、引入
1、关于 zkw 线段树
本人认为:狭义的 zkw 线段树是指建立出满二叉树结构、节点间的父子关系严格规定、一切信息从叶子节点开始向上维护、通过循环递推实现维护过程。
另外:张昆玮大佬的 PPT 中提到,为了减小递归带来的常数,出现了汇编版的非递归线段树。
所以本人的理解是:广义的 zkw 线段树指通过循环递推而非递归实现的线段树。
2、关于优化效果
基于多数线段树结构的特点,导致大部分时候必须上下循环两次维护信息,所以此时 zkw 线段树更多优化的是代码的简洁程度和理解难度(当然了,对常数也有一些优化)。
二、可持久化线段树
1、介绍
可持久化线段树与普通线段树的区别在于,其支持修改和访问任意版本。
举个例子:给定一个序列 \(a_N\),对它进行一百万次操作,然后突然问你第十次操作后的序列信息。
朴素的想法是对于每次操作都建一棵线段树,空间复杂度是 \(O(3mn)\) 的。
可以发现:
修改后,大部分节点并没有受到影响,所以考虑只对受影响的节点新建对应节点。其余没受影响的节点直接与原树共用节点,就等同于新建了一棵修改后的线段树。
2、单点修改单点查询
每次单点修改后,只有叶子节点到根节点的那一条链上的点会受到影响。
所以我们只需要对受影响的这条链新建一条对应的链,其余没受影响的节点直接和待修改版本共用即可。
对于本次要修改的位置,在以原始序列 \(a_N\) 建立的初始线段树中,其对应的叶子节点到根的链上的节点分别为 \(tl\),当前新节点为 \(now\),下一个新节点为 \(new\):
如果 \(tl\) 为左儿子,那么 \(now\) 的左儿子为 \(new\),右儿子为 \(tl\) 对应在待修改树上节点的兄弟节点;
如果 \(tl\) 为右儿子,那么 \(now\) 的右儿子为 \(new\),左儿子为 \(tl\) 对应在待修改树上节点的兄弟节点。
其实就是新建节点的位置与初始树上的节点位置分别对应。
看图(节点内数字为节点编号):在原序列上修改一个位置:
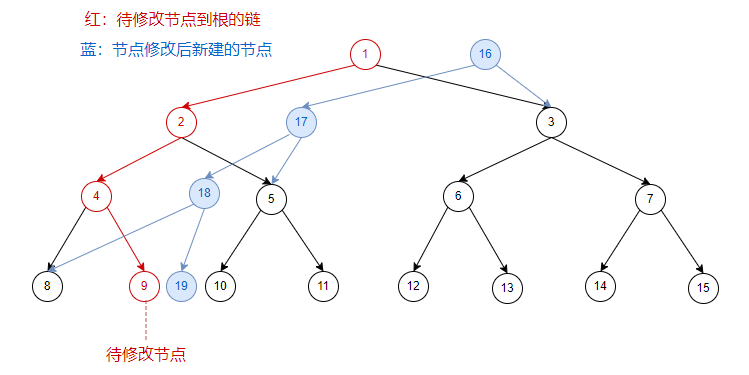
在第一次修改后的序列上,再修改一次:
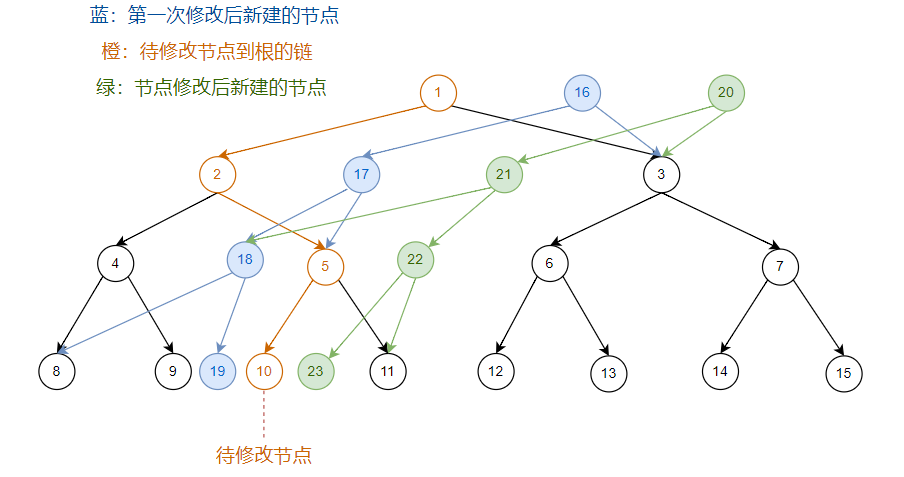
继续在第一次修改后的序列上做修改:
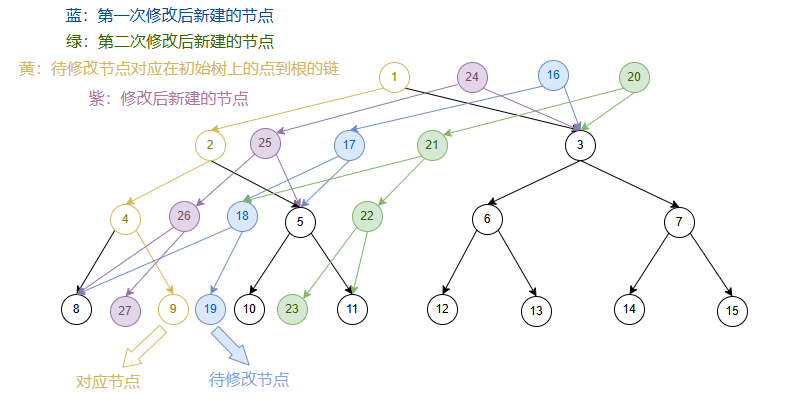
我们发现新建的链在新树上的位置,与初始树上的链在初始树上的位置,是相同的。
所以我们新建节点时,新节点的位置跟随对应的初始树上的节点的位置进行移动。
由于版本间需要以根节点做区分(因为使用叶子节点会非常麻烦),所以修改和查询操作只能从根节点开始自上而下进行,防止不同版本的存储出现问题。
所以我们需要多一个记录:当前节点的左右儿子。
对于 \(tl\) 到根的链如何快速求得,我们前面讲“哨兵”的时候已经讲过实现,接下来就是模拟整个新建节点过程即可。
同时,新建节点的节点编号依次递增,操作后进行自下而上维护信息也很方便:
//建初始线段树
while(P<=n+1) P<<=1,++DEP; NOW = (1<<(DEP+1))-1;//最后一个节点的编号
for(int i=1;i<=n;++i) read(tr[P+i]); rt[0] = 1;//初始树根为1
for(int i=P-1;i;--i) son[i][0]=i<<1,son[i][1]=i<<1|1;//记录子节点 0为左儿子;1为右儿子
//...
//...
inline void update(int i,int vi,int val,int l){
int tl = l+P;//在初始树上对应的叶子节点编号
int v = rt[vi];//待修改线段树的根
rt[i] = l = ++NOW;//新线段树的根
for(int dep=DEP-1; dep>=0 ;--dep,l = NOW){
//模拟节点更新过程
if((tl>>dep)&1) son[l][0] = son[v][0],son[l][1] = ++NOW,v = son[v][1];
else son[l][0] = ++NOW,son[l][1] = son[v][1],v = son[v][0];
}
tr[l] = val;//更新最后的叶子节点
//自下而上维护信息(如果有需要的话)
//for(int dep=1;dep<=DEP;++dep) tr[l-dep]=tr[son[l-dep][0]]+tr[son[l-dep][1]];
}
版本查询与修改相同,从根开始模拟子树选取:
//
inline int query(int vi,int l){
int tl = l+P;//在初始树上对应的叶子节点编号
l = rt[vi];//当前版本的根
for(int dep=DEP-1; dep>=0 ;--dep) l=son[l][(tl>>dep)&1];
return tr[l];//返回叶子节点值
}
3、区间修改区间查询
目前我了解到的信息是:只能做区间加。
可持久化线段树中有大量的公用节点,所以标记不能下放且修改要能够用永久化标记维护,否则会对其他版本产生影响。
那么考虑如何做区间加。
- 标记永久化:省去标记下放以减小常数同时防止对其他版本产生影响;
- 预处理时记录子树大小,查讯时累加标记值。
不同的是:
- 需要对区间新建节点;
- 修改时对照初始树上节点的轨迹进行移动;
- 修改需要自上而下进行,然后再自下而上做一遍维护(类似递归回溯)。
三、权值线段树
1、介绍
普通线段树维护的是信息,权值线段树维护的是信息的个数。
权值线段树相当于在普通线段树上开了一个桶,用于处理信息个数,以单点修改和区间查询实现动态全局第 \(k\) 大。
2、查询全局排名
在权值线段树中,节点存信息出现的次数:
//
inline void update(int l,int k){
l += P; tr[l] += k;//k为信息出现次数
for(l>>=1; l ;l>>=1) tr[l] = tr[l<<1]+tr[l<<1|1];
}
当前数字的相对大小位置向前的前缀和,即为当前数字在全局中的排名:
//
inline int get_rank(int r){//查询第r个数的全局排名
int l = 1+P-1;//做区间[1,r]的前缀和
r += P+1;
int res = 0;
while(l^1^r){
if(~l&1) res+=tr[l^1];
if(r&1) res+=tr[r^1];
l>>=1; r>>=1;
}
return res;
}
3、动态全局第 \(k\) 大
基于线段树的结构,第 \(k\) 大的二分实现其实就在线段树上查找左右子树的过程。
查询第 \(k\) 大时,借助线段树的结构,以左右子树选取来模拟二分过程即可:
//
inline int K_th(int k){
int l = 1,dep = 0;
while(dep<DEP){
if(tr[l<<1]>=k) l=l<<1;//模拟二分
else k-=tr[l<<1],l=l<<1|1;
++dep;
}
return l-P;//减去虚点编号,得到原数组中的编号
}
4、前驱与后继
有时还需要查询 \(k\) 的前驱和后继。
\(k\) 的前驱为:最大的小于 \(k\) 的数;
\(k\) 的后继为:最小的大于 \(k\) 的数。
查 \(k\) 的前驱可以看作:查与 \(k-1\) 的排名相同数;
查 \(k\) 的后继可以看作:查比 \(k\) 的排名靠后一位的数。
结合一下 \(get\_rank\) 和 \(K\_th\) 即可:
//
inline int pre(int k){
int rk = get_rank(k-1);
return K_th(rk);
}
inline int nex(int k){
int rk = get_rank(k)+1;
return K-th(rk);
}
四、可持久化权值线段树(主席树)
有人说 zkw 做不了主席树,我急了。
1、介绍
顾名思义,就是可持久化线段树和权值线段树结合。
大部分情况下只需要支持区间查询,常用于解决静态区间第 \(k\) 大,因为单独的主席树不太好进行修改操作。
当然,动态区间第 \(k\) 大的实现——树套树,可以直接跳到目录五去看。
2、静态区间第 \(k\) 大
主席树对序列的每个位置都维护一棵线段树,其节点值为对应序列上值的范围。
在第 \(m\) 棵线段树上,区间 \([L,R]\) 维护的是:序列上 \(a_i\sim a_m\) 中,有多少数字在 \([L,R]\) 范围内。
我们对序列中每一个数的权值都开一棵线段树,一共开 \(N\) 棵树,存不下,所以使用可持久化线段树。
由于权值线段树存下了数的权值,每个节点上存的是前缀和,信息具有可加性。所以查 \([L,R]\) 等于查 \([1,R]-[1,L-1]\)。
可持久化线段树的新建书和权值线段树的查询结合一下就好了:
//可持久化线段树的建新树
inline void update(int i,int vi,int l,int k){
int tl = l+P;
int v = rt[vi];
rt[i] = l = ++NOW;
for(int dep=DEP-1; dep>=0 ;--dep,l=NOW){
if((tl>>dep)&1) son[l][0] = son[v][0],son[l][1] = ++NOW,v = son[v][1];
else son[l][1] = son[v][1],son[l][0] = ++NOW,v = son[v][0];
}
tr[l] = tr[v]+k;//需要维护前缀和
//向上维护信息
for(int dep=1;dep<=DEP;++dep) tr[l-dep]=tr[son[l-dep][0]]+tr[son[l-dep][1]];
}
//权值线段树的查询
inline int query(int l,int r,int k){
//查 [l,r] 相当于查 [1,r]-[1,l-1]
l = rt[l-1];r = rt[r];
int tl = 1;//答案
for(int dep=0;dep<DEP;++dep){
int num = tr[son[r][0]]-tr[son[l][0]];//左子树大小
if(num>=k){//不比左子树大,说明在左子树中
l = son[l][0];
r = son[r][0];
tl = tl<<1;
}
else{//比左子树大,说明在右子树中
k -= num;
l = son[l][1];
r = son[r][1];
tl = tl<<1|1;
}
}
return tl-P;//当前权值为:对应在初始树上位置减虚点编号
}
五、树状数组套权值线段树
1、介绍
上文说,单独的主席树不方便维护动态区间第 \(k\) 大,主要是因为主席树修改时,对应的其他版本关系被破坏了。
实现动态第 \(k\) 大的朴素想法当然还是对序列的每个位置都开一棵权值线段树,那么难点就在于我们到底要对哪些树做修改。
由于权值线段树具有可加性的性质,所以我们可以拿一个树状数组维护线段树的前缀和,用于求出要修改哪些树。这个过程我们可以用 \(lowbit\) 来实现。
把要修改的树编号存下来,然后做线段树相加的操作,此时操作就从多棵线段树变成了在一棵线段树上操作。
2、初始化
对序列的每个点建一棵 zkw 线段树的话,空间会变成 \(Q(3n^2)\) 的,所以我们需要动态开点,空间复杂度变成 \(O(n\log^2{n})\)。
(存个节点而已,我们 zkw 也要动态开点,父子关系对应初始树就可以了)。
为了保证修改和查询时新树节点与序列的对应关系,以及严格确定的树形结构,所以我们先建一棵初始树(不用真的建出来,因为我们只会用到编号),操作时新树上的节点跟随对应在初始树上的节点进行移动。
//
for(int i=1;i<=n;++i){
read(a[i]);
b[++idx] = a[i];
}
sort(b+1,b+1+idx);
idx = unique(b+1,b+1+idx)-(b+1);//离散化
while(P<=idx+1) P<<=1,++DEP;//求初始树上节点编号备用
for(int i=1;i<=n;++i){
a[i] = lower_bound(b+1,b+1+idx,a[i])-b;
add(i,1);//对每个位置建线段树
}
//...
inline void update(int i,int l,int k){
int tl = l+P,stop = 0;
rt[i] ? 0 : rt[i]=++NOW;//动态开点
l = rt[i]; st[++stop] = l;tr[l] += k;
for(int dep=DEP-1;dep>=0;--dep,st[++stop]=l,tr[l]+=k){
if((tl>>dep)&1) son[l][1]?0:son[l][1]=++NOW,l=son[l][1];
else son[l][0]?0:son[l][0]=++NOW,l=son[l][0];
}
//为了方便也可以把链上的节点全存下来再做维护
//while(--stop) tr[st[stop]] = tr[son[st[stop]][0]]+tr[son[st[stop]][1]];
}
inline void add(int x,int k){//lowbit求需要用到的线段树
for(int i=x;i<=n;i+=(i&-i)) update(i,a[x],k);
}
3、单点修改
先把原来数的权值减一,再让新的数权值加一。
//
inline void change(int pos,int k){
add(pos,-1);
a[pos] = k;
add(pos,1);
}
4、查询区间排名
由于权值线段树维护的是前缀和,所以把区间 \([L,R]\) 的查询看作查询 \([1,R]-[1,L-1]\)。
先用树状数组求出需要用到的线段树,然后做线段树相加,求前缀和即可。
//
inline int query_rank(int l){
l += P;
int res = 0;
for(int dep=DEP-1;dep>=0;--dep){
if((l>>dep)&1){//做线段树相加求前缀和
for(int i=1;i<=tmp0;++i) res-=tr[son[tmp[i][0]][0]],tmp[i][0]=son[tmp[i][0]][1];
for(int i=1;i<=tmp1;++i) res+=tr[son[tmp[i][1]][0]],tmp[i][1]=son[tmp[i][1]][1];
}
else{
for(int i=1;i<=tmp0;++i) tmp[i][0]=son[tmp[i][0]][0];
for(int i=1;i<=tmp1;++i) tmp[i][1]=son[tmp[i][1]][0];
}
}
return res;
}
inline int get_rank(int l,int r,int k){
tmp0 = tmp1 = 0;
for(int i=l-1; i ;i-=(i&-i)) tmp[++tmp0][0] = rt[i];
for(int i=r; i ;i-=(i&-i)) tmp[++tmp1][1] = rt[i];
return query_rank(k)+1;
//query_rank求的是小于等于k的数的个数,加一就是k的排名
}
5、动态区间第 \(k\) 大
和查询排名道理一样:由于权值线段树维护的是前缀和,所以把区间 \([L,R]\) 的查询看作查询 \([1,R]-[1,L-1]\)。
还是先用树状数组求出需要用到的线段树,查询时做线段树相加。然后模拟线段树上二分就可以了。
//
inline int query_num(int k){
int l = 1;
for(int dep=0,res=0;dep<DEP;++dep,res=0){
for(int i=1;i<=tmp0;++i) res-=tr[son[tmp[i][0]][0]];
for(int i=1;i<=tmp1;++i) res+=tr[son[tmp[i][1]][0]];//每棵树的节点值都满足可加
if(k>res){
k -= res;//做树上二分
for(int i=1;i<=tmp0;++i) tmp[i][0]=son[tmp[i][0]][1];
for(int i=1;i<=tmp1;++i) tmp[i][1]=son[tmp[i][1]][1];
l = l<<1|1;
}
else{
for(int i=1;i<=tmp0;++i) tmp[i][0]=son[tmp[i][0]][0];
for(int i=1;i<=tmp1;++i) tmp[i][1]=son[tmp[i][1]][0];
l = l<<1;
}
}
return l-P;//叶子节点对应编号
}
inline int get_num(int l,int r,int k){
tmp0 = tmp1 = 0;//先用lowbit求需要查询的线段树
for(int i=l-1; i ;i-=(i&-i)) tmp[++tmp0][0] = rt[i];
for(int i=r; i ;i-=(i&-i)) tmp[++tmp1][1] = rt[i];
return query_num(k);
}
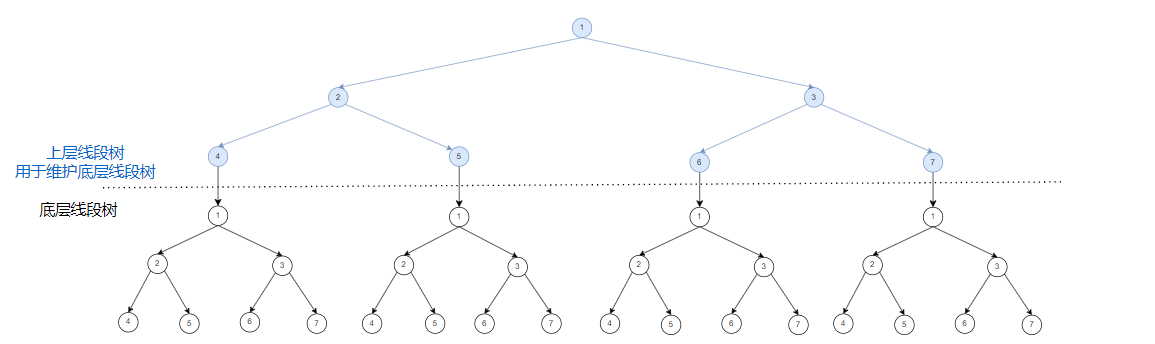
线段树套线段树与其原理相同。下层线段树维护序列信息,再用一棵上层线段树来维护下层线段树的前缀和。
你可以看这张图,我暂时先不多赘述了:(真的码不动字了)
六、兔队线段树
(本人不是特别了解,所以暂时仅作信息具有可加减性的解释)
有人说 zkw 做不了兔队线段树,我急了。
1、介绍
兔队线段树是指一类:在信息修改同时,以 \(O(\log{n})\) 复杂度做维护的线段树。支持单点修改区间查询,通常用来维护前缀最大值的问题。
(粉兔在这篇文章中率先对其进行了说明)
2、处理与维护
其处理与维护信息的大致方式可以看作:
- 首先修改信息,然后从下到上做维护;
- 向上维护时每到达一个节点,都再次从下到上维护信息;
- 第二次从下到上维护时,左子树对答案贡献不变,只考虑右子树对答案的贡献。
由于第一次向上维护时,需要从当前节点开始对其所有子树进行第二次维护,所以递归线段树常用的方法是二次递归处理右子树信息。
3、具体实现
考虑如何用 zkw 线段树递推处理右子树信息。
首先,对单点进行修改后,从下到上进行处理和维护,同时记录节点深度,防止第二次维护时发生越界:
//单点修改后,每次上传更新到根节点
inline void update(int l,ll k){
l += P;int dep = DEP;
mx[l] = k;mn[l] = k;//...
for(l>>=1,--dep; l ;l>>=1,--dep) push_up(l,dep);
}
然后,再次模拟标记上传过程:
//
inline void push_up(int l,int dep){
mx[l] = max(mx[l<<1],mx[l<<1|1]);
//...
ans[l] = ans[l<<1]+calc(l<<1|1,dep+1,mx[l<<1]);
}
inline int calc(int l,int dep,ll mx){
int res = 0,tl = l;
while(dep<DEP){//模拟左右子树选取过程
if(mx[l]<=k) break;//剪枝之类的
if(mx[l<<1]<=k) l = l<<1|1;
else{
res += len[l]-len[l<<1];//信息有可减性,考虑左区间的覆盖
l <<= 1;
}
++dep;
}
if(dep==DEP) res += (mx[l]>k);//叶子节点特判
}
七、Kinetic Tournamen Tree
(有读者评论问能不能实现 KTT,我们讨论研究后发现是可以的。)
1、介绍
KTT 最初在 2020 年集训队论文中由 EI 队长提出。
KTT 用来维护动态区间最大值问题,其基本思想为将需要维护的信息看作一次函数,所有修改都基于函数进行。同时设置阈值,表示维护的答案取值何时发生变化,当修改或查询的信息达到阈值时,暴力重构子树维护答案。
笔者觉得学习 KTT 最好还是从一些具体问题入手。所以我们下文的内容,全部围绕论文中提到的经典问题 P5693 EI 的第六分块进行展开。
2、信息处理
最大子段和要记录四个信息用线段树维护,信息合并时分类讨论:
- \(lmax = \max(lmax_{ls},sum_{ls}+lmax_{rs})\);
- \(rmax = \max(rmax_{rs},sum_{rs}+rmax_{ls})\);
- \(mx = \max(mx_{ls},mx_{rs},rmax_{ls}+lmax_{rs})\)。
进行动态维护就要用 KTT 了,这是我们的重点内容。
现在每个信息记录的都不是一个具体值,而是一条一次函数:\(f(x)=kx+b\)。
其中 \(k\) 为最大子段的长度,\(x\) 为变化量,\(f(0)=b\) 为当前维护的具体值。
同时,对于两条函数,记录一个阈值 \(dx\),表示当前区间最大值是否在两个函数间进行交替。
3、关于交替阈值
前置知识:人教版八年级下册 19.2.3一次函数与方程、不等式
在对两条函数进行合并取最大值时,需要知道具体应该何时选取哪条函数。我们知道应该看函数的交点相对于区间的位置,来对取值情况分类讨论。
交替阈值就干了这样一件事情,维护时记录下何时应该对函数选取进行交替,并只在需要交替时交替,以此优化时间复杂度。
具体地,当区间加 \(q\) 时,函数向上进行了移动,函数的交点相对于区间进行了左右移动。此时我们令阈值 \(dx\) 减小,当 \(dx<0\) 时表示此时选取的函数要进行交替了。
具体减少多少呢,由于函数都满足 \(k\ge 1\),所以至少要令 \(dx-=q\)(当然最好是这个数,减多了重构次数就太多了)。
由于同一个区间可能有两个不同的函数进行维护,所以在合并区间时,阈值不仅要对左右区间取最小值,还需要包含当前两条函数的交点。
4、区间及函数合并
笔者个人建议写成重载运算符形式。
针对函数的操作,有求交点、函数合并、函数移动:
//struct Func
inline Func operator + (const Func&G) const{//函数合并
return Func(k+G.k,b+G.b);
}
inline ll operator & (const Func&G) const{//求交点
return (G.b-b)/(k-G.k);
}
inline void operator += (const ll&G){//函数向上移动
b += k*G;
}
区间合并时,我们在函数操作的基础上分类讨论即可,注意同时维护阈值信息:
//struct Tree
inline bool operator < (const Func&G) const{
//钦定两条函数的相对位置,方便判断有没有交点
return k==G.k && b<G.b || k<G.k;
}
inline void Merge_lx(Func x,Func y,Tree &tmp) const{//求lmax
if(x<y) swap(x,y);
if(x.b>=y.b) tmp.lx = x;//钦定过了函数位置,此时两条函数没有交点
else tmp.lx = y,tmp.dx = Min(tmp.dx,x&y);
}
//...
inline Tree operator + (const Tree&G) const{//区间合并
Tree tmp;tmp.sum = sum+G.sum; tmp.dx = Min(dx,G.dx);//注意维护阈值信息
Merge_lx(lx,sum+G.lx,tmp);Merge_rx(G.rx,G.sum+rx,tmp);
Merge_mx(G.mx,mx,tmp);Merge_mx(tmp.mx,rx+G.lx,tmp);
return tmp;
}
5、修改与重构
区间加按照正常的方式来,唯一不同的是在修改后需要对节点子树进行重构。
首先第一步肯定是下放标记:
//struct Tree
inline void operator += (const ll&G){//区间加
lx += G; rx += G; mx += G; sum += G; dx -= G;
}
//
inline void push_down(int p){//正常push_down
if(tag[p]){
tag[p<<1] += tag[p]; tr[p<<1] += tag[p];
tag[p<<1|1] += tag[p]; tr[p<<1|1] += tag[p];
tag[p] = 0;
}
}
然后再正常做修改:
//
inline void update(int l,int r,ll k){
l += P-1; r += P+1;//先push_down
for(int dep=DEP;dep;--dep) push_down(l>>dep),push_down(r>>dep);
while(l^1^r){
if(~l&1) tag[l^1]+=k,tr[l^1]+=k,rebuild(l^1);//别忘了重构
if(r&1) tag[r^1]+=k,tr[r^1]+=k,rebuild(r^1);
l>>=1;r>>=1;
tr[l] = tr[l<<1]+tr[l<<1|1];
tr[r] = tr[r<<1]+tr[r<<1|1];
}
for(l>>=1; l ;l>>=1) tr[l] = tr[l<<1]+tr[l<<1|1];
}
对于重构,从当前子树的根节点开始一层一层向下递推,直到没有节点需要重构为止:
//
inline void rebuild(int p){
if(tr[p].dx>=0) return ;
int head = 1,tail = 0;
st[++tail] = p; push_down(p);
while(tail>=head){//模拟压栈
int ttail = tail;
for(int j=tail,pos;j>=head;--j){
pos = st[j]; //看子节点的子树是否需要更新
if(tr[pos<<1].dx<0) st[++tail]=pos<<1,push_down(pos<<1);//注意push_down
if(tr[pos<<1|1].dx<0) st[++tail]=pos<<1|1,push_down(pos<<1|1);
}
head = ttail+1;
}//重新维护
do{ tr[st[tail]]=tr[st[tail]<<1]+tr[st[tail]<<1|1]; } while(--tail);
}
6、查询
正常做查询就可以了。
需要注意一点,区间合并时要按照左右顺序进行。
//
inline ll query(int l,int r){
l += P-1; r += P+1;//先push_down
for(int dep=DEP;dep;--dep) push_down(l>>dep),push_down(r>>dep);
Tree resl,resr;
while(l^1^r){
//注意左右区间的合并顺序
if(~l&1) resl = resl+tr[l^1];
if(r&1) resr = tr[r^1]+resr;
l>>=1;r>>=1;
}
return (resl+resr).mx.b;
}
KTT 的基本思路就是这样,将信息转换为函数进行处理,同时维护阈值进行重构。这使得 KTT 有优于分块的复杂度,但同时也对其使用产生了限制。
zkw 实现一些线段树功能
一、线段树优化建图
递归实现要写一车代码,相比之下 zkw 实现显得极致简洁。
1、介绍
当我们需要对一段区间内的点进行连边时,如果对每一点都连一条边,边数是 \(O(n^2)\) 的,往往会炸空间。
我们可以基于线段树的思想,将向区间的每一点连边,改为向一些区间连边,将空间优化为 \(O(n\log{n})\)。
2、入树与出树
构建一棵线段树,每个节点代表一个区间,每个父亲结点向其子节点连一条权值为 \(0\) 的有向边。有向边从父节点连向子节点的叫做出树。
再构建一棵线段树,与出树一样,每个节点代表一个区间。不同的是,每个子节点向其父亲结点连一条权值为 \(0\) 的有向边。有向边从子节点连向父节点的叫做入树。
有时我们只用到其中一种,有时需要两者结合。
当入树与出树配合使用时,需要先对它们对应的叶子节点分别连边(因为它们表示同一个点)且权值为 \(0\),然后再分别做更新。
3、实现
当出树与入树同时使用时,为了区分,我们令入树或出树的节点编号进行整体偏移即可。
//
while(P<=n+1) P<<=1,++DEP;
NOW = (P<<1)-1;//偏移量
for(int i=P-1;i;--i){
add(i,i<<1,0);add(i,i<<1|1,0);//建入树
add((i<<1|1)+NOW,i+NOW,0);add((i<<1)+NOW,i+NOW,0);//建出树
}
//入树与出树的叶子节点连边
for(int i=1;i<=n;++i) add(i+P,i+P+NOW,0),add(i+P+NOW,i+P,0);
- 点向区间连边时,从入树的点向出树的区间连边;
- 区间向点连边时,从入树的区间向出树的点连边。
//点向区间连边
inline void update_dot_intvl(int v,int l,int r,ll w){
l += P-1; r += P+1; v += P;//出树上叶子节点编号
while(l^1^r){
if(~l&1) add(v+NOW,l^1,w);//入树编号有偏移量
if(r&1) add(v+NOW,r^1,w);
l>>=1;r>>=1;
}
}
//区间向点连边
inline void update_intvl_dot(int v,int l,int r,ll w){
l += P-1; r += P+1; v += P;//出树上叶子节点编号
while(l^1^r){
if(~l&1) add((l^1)+NOW,v,w);//入树编号有偏移量
if(r&1) add((r^1)+NOW,v,w);
l>>=1;r>>=1;
}
}
(当然了,有主席树、树套树、zkw 当 ST 表使等等等等等优化方式,根据需求进行选择,作者目前先只对线段树优化建图进行介绍。没时间码字啊。)
二、扫描线
(只讲 zkw 的实现了,过几天再码介绍的字。)
1、介绍
用来求矩形面积并。
将矩形按纵坐标排序,用线段树维护每个位置被图形覆盖的次数以及长度。
向线一样从纵坐标一次自下而上扫一遍。
2、实现
主函数内当然还是先存下信息,然后排序、离散化、然后扫描。
我们来看看线段树内有什么不同。
首先是维护过程。不同与递归线段树,我们可以直接通过节点深度及其编号求出其所管辖的区间。
//len为维护的覆盖长度
inline void push_up(int p,int dep){
if(tr[p].vis){//如果被覆盖了
int l = p<<dep;//管辖的区间的左端点
int r = l+(1<<dep)-1;//根据区间长度求右端点
tr[p].len = b[r-P+1]-b[l-P];
}
else{
if(P>p) tr[p].len = tr[p<<1].len+tr[p<<1|1].len;//非叶子节点
else tr[p].len = 0;//叶子节点
}
}
所以我们在更新的时候,还需要记录当前叶子节点的深度(从下到上啦)用来求其子树内叶子节点的个数。
//
inline void update(int l,int r,int k){
l += P-1; r += P+1; int dep = 0;//记录当前节点深度
// if(l>=r) return ;
while(l^1^r){
if(~l&1) tr[l^1].vis+=k,push_up(l^1,dep);
if(r&1) tr[r^1].vis+=k,push_up(r^1,dep);
l>>=1;r>>=1;++dep;
push_up(l,dep);push_up(r,dep);
}
for(l>>=1,++dep; l ;l>>=1,++dep) push_up(l,dep);
}
于是我们可以省掉记录节点管辖的左右端点的空间。
到现在,能肯定 zkw 线段树基本可以实现递归线段树能做的全部操作了。
一些模板题及代码
后记
更新日志
笔者目前学识过于浅薄,文章大部分内容是笔者自己的理解,可能有地方讲得不是很清楚。等笔者再学会新东西,会先更新在此文章以及我的博客,然后找时间统一更新。
同时,笔者会经常对文章内容细节和代码块进行修改完善,如果您有什么想法可以提出来,我们一起来解决。作者真的真的是活的!!!
期待您提出宝贵的建议。
鸣谢
《统计的力量》清华大学-张昆玮 /hzwer整理
OIWiki
CSDN 偶耶XJX
Tifa's Blog【洛谷日报 #35】Tifa
洛谷日报 #4 皎月半洒花
NianFeng // EntropyIncreaser //
如需转载,请注明出处。


