「笔记」博弈瞎写
想了想还是给这种 blog 取名叫「笔记」比较好。感觉细品来是个很有诗意的名字(我差点就信了)。
没什么干货,基本上都是瞎写,而且是想到什么写什么,所以可能你看完也学习不到什么。
由于我数学很差,所以可能会写大堆废话 + 大堆错误 + 大堆不带证明的结论。
xor
为什么 nim 游戏会与 xor 扯上关系?(虽然就 “验证正确性” 而言这是显然归纳法可证的。。。)
灵感来自于知乎里面的这篇问答。由于知乎的数学公式排版有点难受,所以就自己再梳理了一遍。
首先,我们重新定义 xor 为域 \(\mathrm{Z/2Z}\) 上的线性空间的向量加。相信聪明的读者读到这里已经恍然大悟了,剩下的留作习题。
以下记 \(f(a_1,a_2\dots a_k)\) 表示当前 nim 游戏的 np 状态,其中 \(a_i\) 是第 \(i\) 堆石子的状态。
现在我们想找到 \(1\) 堆石子 \(b\) 等效替代 \(\{a_i\}\),那么有 \(f(b)=f(a_1,a_2\dots a_k)\),由此简化了问题。
为了处理的方便,我们定义 \(\{a_i\}\) 与 \(\{b_i\}\) 等效当且仅当 \(\forall c,f(a_1,a_2\dots a_p,c) = f(b_1,b_2,\dots,b_q,c)\),容易验证这是等价关系。
在等价类之间定义运算 \(A\oplus B = C\),表示把等价类 \(A\) 与等价类 \(B\) 组合得到等价类 \(C\)。这个运算满足:
(1)交换律 \(A\oplus B = B\oplus A\),显然该运算并没有顺序要求。
(2)结合律 \((A\oplus B)\oplus C = A\oplus(B\oplus C)\),由 “等效” 的定义可知。
(3)幺元 \(0\oplus A = A\),显然,因为玩家无法操作没有石子的石堆。
(4)逆元 \(A\oplus A = 0\),由 nim 游戏的对称性策略可得。
也即它是阿贝尔群。事实上,最后一点还说明该群所有元素(除了幺元)都是二阶元素,因此该群同构于一列二阶群的直积。
然后,你发现 xor 也同构于一列二阶群的直积。。。
然后我实在编不下去了,所以暂时留坑吧(
nimber
草nimber这个名字(nim+number)是哪个人才想到的。
定义域 \(F = (N,\oplus,\otimes)\),其中 \(\oplus\) 被称为 nim 和,\(\otimes\) 被称为 nim 积。
\(x \oplus y\) 递归定义为 \(\mathrm{mex}(\{x\oplus b|b<y\}\cup\{a\oplus y|a<x\})\);
\(x\otimes y\) 递归定义为 \(\mathrm{mex}(\{(x\otimes b)\oplus(a\otimes y)\oplus(a\otimes b) |a<x,b<y\})\)。
nim 和的意义是直观的,nim 积的意义。。。可以参考 hdu - 3404。
至于它为什么是域。。。
nim 和的快速求解方法就是 xor,在上面已经有讨论过了。
考虑 nim 积怎么快速求解,先甩几个我也不会证的结论:
(1)\(2^{2^n}\otimes a = 2^{2^n}\times a(a < 2^{2^n})\);
(2)\(2^{2^n}\otimes 2^{2^n} = \frac{3}{2}\times2^{2^n}\);
(3)\(a\otimes b < 2^{2^n} (a < 2^{2^n},b<2^{2^n})\)。
最后一条实际上保证了在 \(<2^{2^n}\) 时 \(F'(S,\oplus,\otimes)\) 形成子域,此时 nim 积逆元可以直接由群论中的拉格朗日定理得到。
如果记 \(a=M\times p_a+r_a,b=M\times p_b+ r_b\),其中 \(p_a,p_b,r_a,r_b<M=2^{2^n}\)。注意到这里的 \(\times,+\) 与 \(\otimes,\oplus\) 结果一致。
为了公式的美观,下文中的 \(\otimes,\oplus\) 全部写成 \(\times,+\)。原本的 \(\times\) 省略不写。
\[\begin{aligned} a\otimes b &= (M\times p_a+r_a)\times (M\times p_b+ r_b) \\ &=(\frac{3}{2}M)\times p_a\times p_b + M(p_a\times r_b+p_b \times r_a)+ r_a \times r_b \\ &=(M+ (\frac{M}{2}))\times p_a \times p_b + M((p_a + r_a)\times (p_b + r_b) + p_a\times p_b + r_a\times r_b)+r_a\times r_b \\ &= (\frac{M}{2})\times(p_a\times p_b)+M((p_a + p_b)\times (r_a + r_b) + r_a \times r_b)+r_a\times r_b \end{aligned} \]中间部分用了分治乘法的技巧,注意 \(\oplus\) 的逆运算就是它自己。
由于 \(p_a,p_b,r_a,r_b<M=2^{2^n}\),所以可以递归到更小的子问题。可以部分记忆化一下优化常数。
时间复杂度 \(T(n)=4T(n-1)=4^n\),而 \(n=O(\log\log a)\),所以 \(T(a) = O(\log^2 a)\)。
typedef unsigned long long ull;
struct nimber{
ull x; nimber() {} nimber(ull _x) : x(_x) {}
friend nimber operator + (const nimber &a, const nimber &b) {
return nimber(a.x ^ b.x);
}
friend nimber mul(const nimber &a, const nimber &b, int L) {
if( a.x <= 1 || b.x <= 1 ) return a.x * b.x;
ull M = (1ull << L);
nimber pa = (a.x >> L), ra = (a.x & (M - 1));
nimber pb = (b.x >> L), rb = (b.x & (M - 1));
if( pa.x == 0 && pb.x == 0 ) return mul(a, b, L >> 1);
nimber p = mul(pa, pb, L >> 1), q = mul(pa + ra, pb + rb, L >> 1), r = mul(ra, rb, L >> 1);
return mul(M >> 1, p, L >> 1) + nimber(M * (q + r).x) + r;
}
friend nimber operator * (const nimber &a, const nimber &b) {
return mul(a, b, 32);
}
friend nimber mpow(nimber a, ull p) {
nimber r; for(r = 1; p; p >>= 1, a = a * a)
if( p & 1 ) r = r * a;
return r;
}
friend nimber operator / (const nimber &a, const nimber &b) {
return a * mpow(b, (ull)-2);
}
};
最后放一张 wiki 上关于 nim 积的图片吧。数学真美啊.jpg。

surreal number
在非平等组合游戏中,我们分别称两个玩家为左玩家与右玩家(一般来说只考虑有限游戏 无穷的我也不会)。
记 \(x+y\) 表示同时进行游戏 \(x, y\) 得到的游戏。
记 \(-x\) 表示交换左右玩家地位得到的游戏;记 \(0\) 表示空游戏,即左右玩家都无法操作的游戏。
记 \(x=0\) 当且仅当 \(x\) 后手必胜;记 \(x>0\) 当且仅当 \(x\) 左玩家必胜;记 \(x<0\) 当且仅当 \(x\) 右玩家必胜。
记 \(x<y\) 当且仅当 \(x+(-y)<0\),表示 \(y\) 比 \(x\) 对于左玩家更有优势。类似地也可以得到 \(>,=,\geq,\leq\) 等关系。
需要注意,这里的 \(=\) 符号描述的是一个等价类,即使两个游戏 \(x,y\) 不完全相同,也可以有 \(x=y\)。
以上记法是 “直观” 的,但是非常不严谨,甚至 \(<\) 都不是良定义的偏序关系。
对于游戏 \(x\),左玩家走一步得到的所有游戏构成集合 \(X_L\),右玩家走一步得到的所有游戏构成集合 \(X_R\)。记 \(x=\{X_L | X_R\}\)。
对于所有 \(\forall p\in X_L, q\in X_R,p<q\) 的游戏,它们的运算法则和有序域 surreal number 一模一样。
有限元素组成的 surreal number 同构于二进分数域(即分母为 \(2^k\) 的有理数),因此关于 surreal number 的其他性质 全 部 木 大,我们只需要找到 游戏/surreal number \(\to\) 二进分数 的同构映射即可。
一些补充定义/结论:
若 \(x=\{X_L | X_R\}\),则 \(x = \{\max X_L | \min X_R\}\)(只适用于有限情况,无穷情况可能不存在最值)。从博弈的角度去理解,即左玩家总会选择对自己优势最大的决策;右玩家同理。
若 \(x = \{a|b\}\),则 \(a<x<b\)。
\(x+y = \{(X_L+y)\cup(x+Y_L)|(X_R+y)\cup(x+Y_R)\}\),其中 \(X+y=\{p+y|p\in X\}\),\(x+Y=\{x+p|p\in Y\}\)。
\(-x=\{-x_R|-x_L\}\);\(0+x=x\);\(x+(-x)=0\)。
接下来考虑怎么求,假设我们已经将 \(x\) 简化为 \(x=\{a|b\}\) 的形式:
从 \(S_0=\{0\}\) 开始,第 \(i\) 次从 \(S_{i-1}\) 里面任意选 \(a, b\) 并把 \(\{a|b\},\{a|\},\{|b\},\{|\}\) 加入 \(S_i\)。
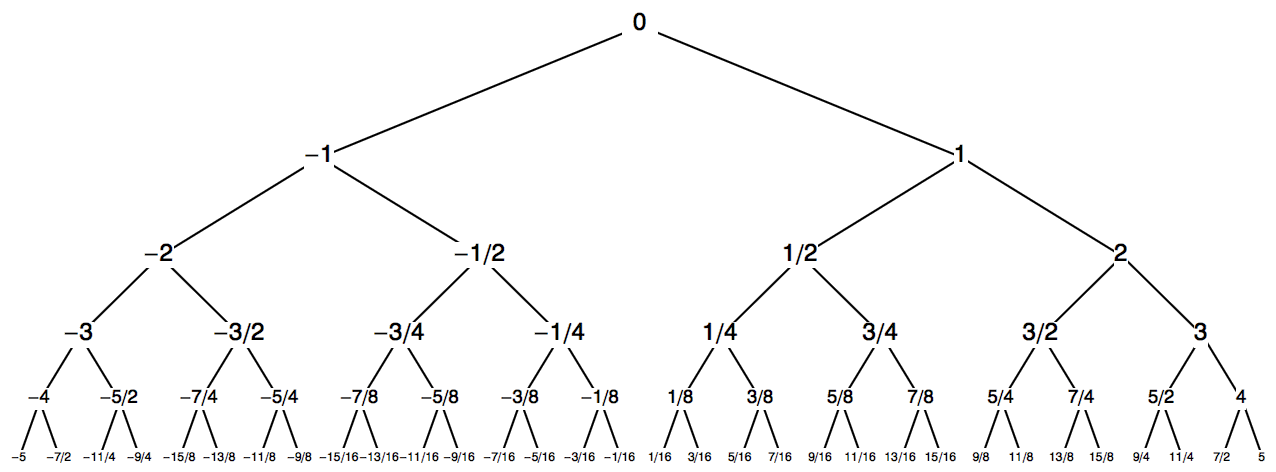
那么可以构造出如下的二叉搜索树(其中第 \(i\) 层表示 \(S_i\setminus S_{i-1}\)):
可以证明:若 \(x=\{a|b\}\),则 \(x\) 是开区间 \((a,b)\) 在这棵二叉搜索树上对应的最高点(注意是开区间)。
实际操作时,为了方便,我们把空集记作 \(\pm\infin\),比如 \(0=\{-\infin|+\infin\}\)。
我们可以先讨论 \((a,b)\) 内有没有整数,如果有则取绝对值最小的整数;否则取分母最小的二进分数。
你以为这样就结束了?注意我们只讨论了 \(x=\{a|b\}\) 中 \(a<b\) 的游戏。
定义 \(*=\{0|0\},\uparrow=\{0|*\},\downarrow=\{*|0\}\),尽管这些游戏无法被表示成 surreal number,但是它有存在的价值,比如 \(*\) 对应了一种先手必胜的游戏。
关于这几个符号之间的运算 由于我不想看英文所以 没找到比较全面的,只有一些:
\(*+*=\uparrow + \downarrow = 0\);\(\{\uparrow|\downarrow\} = *\);
\(\forall x>0,-x<\downarrow<0<\uparrow<x\);
\(\forall x > 0, * + x > 0\);\(\forall x < 0, * + x< 0\);
\(\uparrow+*\) 为先手必胜态;\(\uparrow + \uparrow + * > 0\)。
wythoff
其实是因为之前做到了这道题,就想来写写。
有两堆
古明地恋小石子,第一堆有 \(a\) 颗,第二堆有 \(b\) 颗。有两个人在博弈,每次操作可以从一堆石子中取走任意数量个,或者从两堆石子中取走 \(x, y\) 个,要求 \(|x-y|\leq k\),不能操作者输。
问先手是否有必胜策略。
当 \(k = 0\) 时就是一般形式的 wythoff 博弈。
然后我们打表打出所有必败态 \((a_i, b_i)(a_i\leq b_i,i\geq 0)\) 分析一下,发现 \(a_i=\mathrm{mex}\{a_j,b_j|j<i\}\),\(b_i = a_i+(k+1)i\)。
betty 定理:
设 \(\alpha , \beta\) 是正无理数且 \(1/\alpha + 1/\beta = 1\),令 \(P=\{\lfloor \alpha n\rfloor |n\in N^+\}, Q=\{\lfloor \beta n\rfloor |n\in N^+\}\),则 \(P\cap Q = \empty\and P\cup Q = N^+\)。
丢个链接就逃(
由于必败态其实也覆盖了所有正整数,所以可以往 betty 定理靠:
令 \(a_n = \lfloor \alpha n\rfloor\),\(b_n = \lfloor \beta n\rfloor\)。则有 \(\lfloor \alpha n\rfloor + (k+1)n= \lfloor \beta n\rfloor\),即 \(\lfloor (\alpha + k + 1)n\rfloor= \lfloor \beta n\rfloor\)。
因此得到 \(\alpha + k + 1 = \beta\),联立一下解出 \(\alpha, \beta\) 即可。
挺奇妙的(