「某补题记录」
contest 1
1001 Avian Darts(咕)
不是很懂三维空间角速度怎么合成的,改天问一下隔壁物竞的同学吧,先咕了。
update:问了,他们表示没听懂我在说什么。
1002 Boring Task(咕)
下次一定吧。1007 把我人都搞没了。
1003 Cookies
从后往前处理,第 \(i\) 天第 \(k\) 块以前会有 \(\lfloor\frac{k-1}{p_i-1}\rfloor\) 块被吃掉,加上这个值即可。
考虑怎么求 \(f_n\),首先 \(divmed(n)\) 的等价定义为 \(\leq \sqrt{n}\) 的最大因子。
It’s difficult to get the value directly in reasonable time.
考虑分段打表,本地跑出 \(f_{2.5\times10^6i}\)(p.s.:hdu 代码限制 64K),跑个十分钟就跑出来了。存差分值好像代码长度要短些。
考虑怎么求 \(divmed(l\dots r)\),发现用埃氏筛即可。
1004 Distinct Sub-palindromes
1005 Fibonacci Sum
模 \(10^9 + 9\) 意义下 \(5\) 有二次剩余,斐波那契通项公式 + 等比数列求和。
1006 Finding a MEX
度数 \(>B\) 的用 set 维护;度数 \(\leq B\) 的询问时暴力查。取 \(B=O(\sqrt{n\log n})\) 最优。
【以上是现场莽过去的做法】
大点修改 \(O(\log n)\),询问 \(O(\log n)\),考虑平衡一下;使用分块可以做到修改 \(O(1)\),询问 \(O(\sqrt{n})\),总时间复杂度 \(O(n\sqrt{n})\)。
由于大块的度数和为 \(O(n)\),所以可以对所有大点一起分。
1007 Hunting Monsters
考虑固定砍哪些怪物,怎样安排顺序最优。这是个经典贪心问题:所有 \(a_i\leq b_i\) 的排在 \(a_i > b_i\) 的前面;\(a_i \leq b_i\) 的内部按 \(a_i\) 从小到大排;\(a_i > b_i\) 的按 \(b_i\) 从大到小排。
先按这个法则排好序,显然有朴素 dp:\(f_{i,j}\) 表示后 \(i\) 个选 \(j\) 个砍的最小初始体力,转移式:
为了方便优化,我们不妨先把 \(a_i\leq b_i\) 与 \(a_i > b_i\) 分开考虑。
先考虑 \(a_i>b_i\),显然 \(f_{i,j-1}\leq f_{i,j}\) 且 \(f_{i,j}\leq f_{i-1,j}\)。
考虑 \(\max\{f_{i-1,j-1}+a_i-b_i,a_i\}\) 的取值,它决定于 \(f_{i-1,j-1}\) 与 \(b_i\) 的大小关系。
由于 \(f_{i,j-1}\leq f_{i,j}\),所以存在 \(j_0\) 满足 \(j\leq j_0\) 时 \(f_{i-1,j-1} \leq b_i\);\(j > j_0\) 时 \(f_{i-1,j-1} > b_i\)。
注意到 \(f_{i,j}\leq f_{i-1,j}\) 且 \(b_{i} \leq b_{i+1}\)(一开始的贪心性质,注意我们是从后往前 dp),则 \(j_0\) 随 \(i\) 增大而增大。
对于 \(j<j_0\),有 \(f_{i-1,j-1} \leq b_i\) 且 \(f_{i-1,j}\leq b_i < a_i\),故 \(f_{i,j}=f_{i-1,j}\)。
对于 \(j = j_0\),\(f_{i,j}=\min\{f_{i-1,j},a_i\}\)。
对于 \(j>j_0\),\(f_{i,j}=\min\{f_{i-1,j},f_{i-1,j-1}+a_i-b_i\}\)。它的值取决于 \(f_{i-1,j}-f_{i-1,j-1}\) 与 \(a_i - b_i\) 的大小关系。
考虑加入虚点 \(f'_{i-1,j_0-1}=b_i\) 来统一 \(j\geq j_0\) 的形式,得到 \(f_{i,j_0}=\min\{f_{i-1,j_0},f'_{i-1,j_0-1}+a_i-b_i\}\)。
因此不难想到当 \(j \geq j_0\) 时 \(f_i\) 应该是凸的,即 \(f_{i,j}-f_{i,j-1}\leq f_{i,j+1}-f_{i,j}\)。至于怎么证。。。
This convexity can be proved by mathematical induction on 𝑖. Try yourself and have fun.
考虑 \(f_{i,j}=f_{i-1,j-1}+a_i-b_i\) 的含义:即点 \((j-1,f_{i-1,j-1})\) 平移到 \((j, f_{i-1,j-1}+a_i-b_i)\)。
可以看作在凸函数内部的合适位置(即保持斜率单调的位置)加入向量 \((1,a_i-b_i)\),因此直接优先队列维护即可。
实现时一个很恶心的细节就是:为了正确维护与虚点之间的斜率,你可能要先把优先队列头弹出来改正确后再放回去(调了我一晚上调出来的)。
考虑 \(a_i \leq b_i\),显然砍排序后的前几个最优(草本来觉得很显然,仔细一想突然发现自己并不会证)。
设 \(g_i\) 表示砍前 \(i\) 个最小初始体力,\(h_i\) 表示砍完前 \(i\) 个的体力增量,显然有 \(g_i\leq g_{i+1},h_i\leq h_{i+1}\)。
考虑如何合并答案:\(ans_k=\min_{i+j=k}\{\max\{g_i, f_{p,j}-h_i\}\}\)。可以考虑枚举 \(g_i\),记 \(last\) 为上次赋值的最后位置。
先算 \(f_{p,j}-h_i\leq g_i\) 的最大 \(j\),则 \(ans_{last+1\dots i+j} = g_i\) 并更新 \(last\);再算 \(f_{p,j}-h_i\leq g_{i+1}\) 的最大 \(j\),则 \(ans_{last+1\dots i+j}=f_{p,j}-h_i\)。
1008 Integral Calculus
记 \(f(N) = \int_{0}^{+\infin}\frac{x^{-2N-1}}{e^{\frac{1}{x}}-1}dx\),则答案为 \(\frac{f(2N)}{f^2(N)}\)。
换元 \(t=x^{-1}\),得到 \(f(N)=\int_{0}^{+\infin}\frac{t^{2N-1}}{e^t-1}dt\)。
尝试凑出 \(\Gamma(N)=\int_{0}^{+\infin}t^{N-1}e^{-t}dt\)。由于 \(\frac{1}{e^t-1}=\frac{1}{1-e^{-t}}-1\),而 \(t > 0 \Rightarrow e^{-t} \in (0, 1)\),因此得到 \(\frac{1}{e^t-1}=\sum_{i=1}^{\infin}e^{-it}\)。
故:
然后在知乎上查一查有 \(\zeta(2N) = \frac{(-1)^{N+1}\times B_{2N}\times(2\pi)^{2N}}{(2N)!\times2}\),其中 \(B_i\) 为伯努利数。
因此有 \(f(N)=\frac{(-1)^{N+1}\times B_{2N}}{4N}\times(2\pi)^{2N}\),答案为 \(-\frac{B_{4N}}{B_{2N}}\times 2N\)。
于是 mtt + 多项式求逆即可。有点卡常,小范围暴力求逆 + 抄标程的 fft 过了。
1009 Leading Robots
\(x_i=p_i+\frac{1}{2}a_it^2\),作换元 \(u = t^2\) 变成直线 \(x_i=\frac{a_i}{2}\times u + p_i\),凸包/半平面交即可。
1010 Math is Simple
作如下定义:
先抛结论:\(f_n = g_n + \frac{1}{2}\)。
考虑对 \(g_n\) 裂项,得到:
考虑建立 \(f_n\) 与 \(f_{n-1}\) 的递推式,得到:
也即 \(f_n = f_{n-1}+g_n-g_{n-1}\),边界条件 \(f_2 = \frac{1}{2}\)。代一代发现 \(f_n=f_2+g_n-g_2=g_n+\frac{1}{2}\),因此证毕。
求 \(g_n\) 反演即可,预处理一下 \(10^8\) 以内的调和级数。
1011 Minimum Index
lyndon 分解后取最后一个 lyndon 串即是答案。
观察 Duval 算法的过程,最后分解得到了近似 lyndon 串 \(ww\dots \overline{w}\)。
如果 \(\overline{w}=\empty\) 则 \(ans_i=|w|\);否则 \(ans_i = ans_{i-|w|}\)。
1012 Mow
先内缩凸多边形得到圆心范围:将边向内平移 \(r - \epsilon\) 再半平面交。
然后外扩多边形得到圆形扫过的面积,即缩后的凸多边形 + 若干矩形 + 若干扇形。
contest 2
丢人现场.jpg。
1001 Total Eclipse
【一些小彩蛋】
一开始 clarification 里面有:
Reply To:Do we should make sure the k is as maximum as possible?
not necessary
admin at 2020-07-23 13:41:25
结果好像后来有人出了一组数据把 std hack 了。
于是就在题目里面加了这句话:
Note that Sunset will always choose k with the maximum possible value.
所以就变成了按 \(b\) 从大到小倒着做的经典并查集应用了。
1002 Blood Pressure Game
经典 dp:按权值从小到大加入,状态记录当前有多少连续段,以及是否有连续段是最终序列的首/末位置。
求前 k 大,那么 dp 转移时用归并即可。
1003 Count on a Tree II Striking Back
由于种种原因,考虑随机化。
给每种颜色一个随机权值,颜色种类越多,则颜色权值最小值越小。
因此随机个 \(k = 30\) 次左右即可判断两条链谁多谁少,链查询最小值可以树剖 \(O(\log^2 n)\) 也可以全局平衡二叉树 \(O(\log n)\)。
总复杂度 \(O(n+mk\log n)\) 或 \(O(n+mk\log^2n)\)。草凭什么全局平衡二叉树跑得没树剖快啊。
submission(由于系统rand较慢,手写随机数效率更高)。
1004 Diamond Rush
(容我先抱怨一句,这道题的下发数据包好像是错的,调到意识模糊后测一下标程才发现不对。。。)
一看这不是用二维st可以O(nq)吗,然后rush了一波发现TLE了。
如果不考虑权值范围,可以先两遍 dp 求出起点到某点、某点到终点的最大权,从而求出必须经过某个点的最大权,然后询问可以这么拆解:
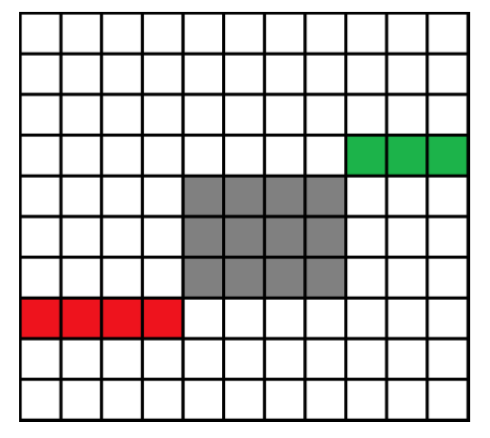
必须经过其中某个红点/绿点,所以预处理一下红点与绿点的最大值即可。
考虑权值很大怎么比,发现其实就是比 \(n^2\) 进制下两字符串的大小,hash 即可。可持久化线段树维护一下 dp 转移时 hash 的更改。
注意不能把起点到某点、某点到终点的最大权直接合并,在比较时同时传两个参数即可。时间复杂度 \(O((n^2+q)\log n)\)。
1005 New Equipments
显然最小权匹配,建图时连二次函数最低点 + 周围 n 个点,然后直接费用流(惊讶发现spfa也能过)。
1006 The Oculus
判大数相等是哈希经典例题,比如古老的 noip2014 解方程。选个模数然后在模意义下判是否相等即可
1007 In Search of Gold
二分答案 + 树形 dp。通过经典 trick 可以做到 \(O(nk\log A)\)(实测k^2被卡)。
1008 Dynamic Convex Hull
外层线段树分治,内层我赛场上写的是将四次函数沿对称轴分成两个单调函数,然后用李超线段树。
虽然理论 \(O(n\log^3 n)\) 不过由于李超线段树跑不满所以过了。
理论复杂度正确的做法是如果询问 \(x\) 则将函数分为 \(a_i<x\) 与 \(a_i\geq x\) 两类,两类分别满足单调性,于是在线段树中每个结点做决策单调性(或者也可以李超线段树)即可做到 \(O(n\log^2n)\)。
1009 Lead of Wisdom
冷静一下,发现时限 8s,于是你写了个暴搜结果交上去TLE。
把对应物品数量为 0 或 1 的种类单独处理,剩下的暴搜就过了。
1010 It's All Squares
暴 力 能 过,震 撼 百 年。
考虑处理出多边形上下左右边界,然后扫一遍边界内的点看是否在多边形内(用射线法,引水平线即可)。
冷静分析时间复杂度:边长为 \(C\) 的多边形最多包含 \(\frac{C^2}{4}\) 个点(那这不是O(|S|^2)吗),注意到总区域长宽只有 \(O(n)\),因此总复杂度应该是 \(O(|S|\times n)\)(还要除以 4 的常数就十分科学) 。
1011 King of Hot Pot
【由于没看懂题解所以只能附上自己丑陋的解法】
显然应该按 \(a_i\) 从小到大吃,同时还注意到第 \(k-1\) 个最优解一定是第 \(k\) 个最优解的子集。
考虑从第 \(k-1\) 到第 \(k\),此时有一些时间区间已经被占用。如果 \([l, r]\) 被占用且 \(a_i\in [l, r]\),则可以等价地认为 \(a_i = r\)。
由于我们总是按最优的来转移,所以 \((a_i, b_i)\) 对应的解一定包含它之后的所有被占用区间,因此它贡献为这些区间长度和 + \(b_i\)。
考虑怎么维护:将 \(a_i\in[l, r]\) 的所有 \((a_i,b_i)\) 放在一起,内层可并堆维护 \(b_i\) 的最小值,外层套平衡树,这样是 \(O(n\log n)\) 的。
1012 String Distance
预处理 \(pre_{c,i}\) 表示 \(A\) 串中位置 \(i\) 之前第一个字符 \(c\) 的出现位置。
询问时求 \(f_{i,j}\) 表示 \(B[i\dots m]\) 匹配 \(A[1\dots r]\) 得到公共子序列长 \(j\) 时能匹配到的最靠近 \(r\) 的位置,用 \(pre\) 递推可以做到 \(O(qm^2)\)。
contest 3
rush 到最后一分钟居然过了。很开心。
1001 Tokitsukaze, CSL and Palindrome Game
赛后一看Clarification才发现题目中说的firstly是指自己的第一次,与对手无关,草。
利用概率生成函数可以得到 \(E(S)=\sum_{i=1}^{|S|} [S_{1\dots i}=S_{|S|-i+1\dots |S|}]\times 26^i\),可以看成一个 \(26\) 进制数。
比较 \(E(S_{a\dots b})=E(S_{c\dots d})\) 可以在 \(26\) 进制下由高位开始比较。
在回文树上定位该串,利用 \(border\) 的 \(O(\log)\) 等差数列性质可以做到 \(O(n\log n)\) 的复杂度。
1002 Lady Layton and Stone Game
(0)每次一定挑最小的若干个合并。
(1)最优解合并次数一定是所有可行解中最少的。
(2)最优解中,只会存在最多一次合并 \(x\not=L,R\) 个,其他次合并要么合并 \(L\) 个,要么合并 \(R\) 个。
(3)最优解中,合并的个数一定是逐渐增多,即先合并若干次 \(L\) 个再合并 \(x\) 个再合并若干次 \(R\) 个。
全 部 不 会 证。
那么先找到最小的 \(p\) 满足 \(\sum a_i - 1\leq (R-1)p\),如果 \((L-1)p\leq \sum a_i - 1\) 则有解,否则无解。
二分出合并 \(L\) 的次数、\(x\)、合并 \(R\) 的次数,然后模拟即可(注意跑 huffman 时有一个不用优先队列的解法)。
假如第 \(i\) 种有 \(a_i\),合并一次最多剩下 \(\lceil\frac{a_i}{L}\rceil\),因此每种数最多 \(O(\log a)\) 次,所以总复杂度 \(O(n\log a)\)。
1003 Tokitsukaze and Colorful Tree
离线后分每种颜色处理(然后赛场上我队友就被我忽悠去对于每种颜色建了棵虚树,然而并不必要)。
对于某种颜色,操作为加入/删除权值,查询可以取补集变为 总贡献 - 祖先关系贡献。
对异或拆位,每一位都是单点修改 + 子树/到根的链查询,后一个可以变为子树修改 + 单点查询,因此直接在 dfs 序上树状数组即可。
总时间复杂度 \(O(n\log A\log n)\) (然后我就被愉快地卡常了),研究一下发现可以把 6 次树状数组操作缩成 4 次,然后就过了(但还是排行榜最慢)。
1004 Tokitsukaze and Multiple
记 \(l_i = \max\{x\}(x<i,a_{x}=a_i\bmod p)\),则原题即选择最多不相交线段 \([l_i, i]\),贪心即可。
队友的做法,太复杂请不要喷我,因为我也觉得做复杂了。
1005 Little W and Contest
并查集基础应用。
1006 X Number
显然数位 dp。
预处理出 \(f(s,i,p)\),其中 \(s = \{a_{0\dots 9}\},a_0\leq a_1\leq \dots \leq a_9\) 表示当前已知的位置 \(0\sim 9\) 的出现次数的排序结果,想要最大化 \(a_i\) 对应的数字,剩下 \(p\) 个空位置可以放。
由于 \(s\) 的种类 \(< 1500\),所以暴力做即可。注意讨论前导零。
1007 Tokitsukaze and Rescue
又是暴力能过。震撼,震撼。
枚举 \(k\) 条边删掉重跑最短路 不过显然是TLE的,注意到每次删 \(1\sim n\) 的最短路上的边才有用 于是竟然就这样过了。
因为边权随机,最短路上的边数实际上很少。
1008 Triangle Collision
可以让球一直跑直线,然后三角形外框平面密铺。
二分答案后即判线段与三组等距平行线的交点个数,随便做即可。
1009 Parentheses Matching
先把能匹配的括号匹配了,剩下形如 ")))...(((" 的形式,然后尽量把靠左的 '*' -> '(',把靠右的 '*' -> ')'。
1010 Play osu! on Your Tablet
定义 \(f(i, j)\) 表示处理完前 \(i\) 个,一只手滑到了点 \(i\),另一只手滑到了点 \(j(j<i)\)。
转移两类,第一类 \(f(i, j) + dis_{i,i+1}\to f(i+1,j)\);第二类 \(f(i, j)+dis_{j,i+1}\to f(i+1,i)\)。
第一类全局打 tag,第二类查询 \(f(i,j)+dis_{j, i+1}\) 的最小值,即单点修改 + 二维平面查询,KD-tree 即可。
在 KD-tree 上跑的时候加了点最优性剪枝好像跑得飞快。
1011 Game on a Circle
大体思路类似于「PKUWC2018」猎人杀。
记 \(f_i\) 表示恰好有 \(i\) 个在 \(c\) 之后删掉,记 \(g_i\) 表示钦定有 \(i\) 个在 \(c\) 之后删掉,已知 \(g\) 可以二项式反演得 \(f\)。
记 \(h_{i, j}\) 表示 \(i\) 个石子的环,其中 \(c\) 排第 \(j(1\leq j \leq i)\) 个,使得 \(c\) 被第一个删除的概率。
则有 \(h_{i,j}=(1-p)^{j-1}\sum_{k=0} (1-p)^{ik}\times p=\frac{(1-p)^{j-1}\times p}{1-(1-p)^i}\)。
则 \(g_i = \sum_{j<c,k\leq n-c}^{j+k=i}\binom{c-1}{j}\binom{n-c}{k}h_{i+1,j+1}\),把 \(h\) 的表达式代入可以得到两个式子卷积的形式,直接 ntt 即可。
(看了 solution,好像最后一步可以微分建立 \(g_i\) 的递推式,可以少一次卷积)
contest 4
自闭。
不知道队友怎么在写 1003 的随机化,交了十几二十发都过不了。
自己这边 1009 搞了半天没搞出来,不知道在想什么。
差点掉出前 100,丢人啊。
1001 Anti-AK Problem(咕)
好一手anti-ak。球面几何啥的完全看不懂。
1002 Blow up the Enemy
暴力枚举就能过了。也可以对于每个武器算出击杀时间,贪心选择最短击杀时间的武器。
1003 Contest of Rope Pulling
你永远也不知道为什么赛后你写一写就 A 的题,赛场上队友们交了 20+ 都过不了。
问题即 \(n + m\) 个物品的 01 背包问题,其中 \(m\) 个物品的体积为负,求体积为 0 时的最大权和。
由于背包是 np 问题所以我们考虑随机化:将物品打乱塞入背包,并设置一个阈值 \(L\) 使得 dp 过程中状态在 \([-L, L]\) 中。
这样时间复杂度为 \(O(nL)\),我取的 \(L = 1.5\times 10^5\)。题解证明了这个过程的正确概率很高(但是感觉没什么用就不写了)。
1004 Deliver the Cake
拆点最短路。
1005 Equal Sentences
显然 dp。判字符串不知道为啥队友们是用的 hash,明明暴力就好了。
1006 Fake Photo(咕)
没什么理由就是不想写。
1007 Go Running
\(t_{i}-x_{i}\) 相等的可以放一起;同理 \(t_i + x_i\) 相等的可以放一起。
考虑建二分图 \((t_i-x_i)\to(t_i+x_i)\),则该二分图的最小点覆盖即为答案。跑 dinic 即可。
1008 Head Maker(咕)
没什么理由就是不想写。
1009 Imperative Meeting
被降智惹 QAQ。
对于每条边算贡献,假设该边连接了大小为 \(s,n-s\) 的两棵子树,则贡献为 \(\sum_{i=0}^{m}\min\{i,m-i\}\times\binom{s}{i}\binom{n-s}{m-i}\)。
记 \(t_1 = \lfloor\frac{m}{2}\rfloor, t_2=\lfloor\frac{m-1}{2}\rfloor\),则贡献等于 \(\sum_{i=0}^{t_1}i\times\binom{s}{i}\binom{n-s}{m-i}+\sum_{i=0}^{t_2}i\times\binom{s}{m-i}\binom{n-s}{i}\),由此去掉了 \(\min\)。
由于 \(g_{n,m,t}(s)=\sum_{i=0}^{t}i\times\binom{s}{i}\binom{n-s}{m-i}=\sum_{i=0}^{t}s\times\binom{s-1}{i-1}\binom{n-s}{m-i}\),如果求出 \(f_{n,m,t}(s) = \sum_{i=0}^{t}\binom{s}{i}\binom{n-s}{m-i}\),则 \(g_{n,m,t}(s)=s\times f_{n-1,m-1,t-1}(s-1)\)。
考虑递推 \(f_{n,m,t}(s-1)\to f_{n,m,t}(s)\)。联系 \(f\) 的组合意义,可得 \(f_{n,m,t}(s)-f_{n,m,t}(s-1)=\binom{s-1}{t}\binom{n-s}{m-t-1}\)。
1010 Joyful Party(咕)
不是,哪有拿员交的东西当比赛题目的啊。
1011 Kindergarten Physics
你甚至可以在知乎上搜到这样一个问答,然后在里面发现一条公式:
不过这是 \(t\) 关于 \(s\) 的表达式,于是你需要二分一下。
然而由于万有引力实在太小了,所以你其实只需要输出 \(d\) 即可。
1012 Last Problem
这。。。构造题要我写什么。
直接把代码 copy 过来吧(逃
#include <bits/stdc++.h>
using namespace std;
void print(int x, int y, int c) {printf("%d %d %d\n", x, y, c);}
void write1(int x, int y, int c) {
if( c > 4 ) write1(x + 1, y, c - 4);
print(x, y, c);
}
int main() {
int n; scanf("%d", &n);
for(int i=0;i<n;i++) {
int p = i / 2;
for(int j=0;j<p;j++)
write1(i, p - j, j * 2 + (i % 2) + 1);
p = i / 3;
for(int j=0;j<p;j++)
write1(i, j - p, j * 3 + (i % 3) + 1);
if( i >= 4 ) write1(i + 1, 0, i - 3);
print(i, 0, i + 1);
}
}
contest 5
我给全队提供了 11 次罚时。我忏悔。
大概补题速度会变慢(因为懒)。
update:这出题人是有多喜欢二合一啊。1002,1004,1010,1013 全是二合一题。
1001 Tetrahedron
草,我队友好像是建系算的。
省略建系暴算过程,最后得到 \(\frac{1}{h^2} = \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2}\)。
1002 Funny String
预先跑个后缀数组。
如果在前面加字符,分两类:一是查询 1,在后缀数组上二分;二是查询 2~n+1,讨论新后缀与它的大小关系即可。
如果在后面加字符,一样分两类:一是查询 n+1,预处理每种字符出现次数前缀和;二是查询 1~n,除了要讨论新后缀与它的大小关系,原先的关系可能会改变。
考虑如果原先 \(suf_i < suf_j\),末尾加入字符 \(c\) 后 \(suf_i>suf_j\)。此时 \(suf_i\) 一定是 \(suf_j\) 的前缀,且 \(S_{j+n-i+1} < c\)。
对反串跑 z-algorithm,则变成对区间的 \(S_{i+1}\) 位置 \(\pm 1\)。可持久化线段树即可,总复杂度 \(O(n\log n)\)。
不理解啊,为什么我算出来需要3nlogn的空间然后2nlogn就过了,3nlogn就MLE了。
1003 Boring Game
按题意模拟。
1004 Expression(咕)
偏导不会,咕了。
1005 Array Repairing
草,我怎么又做了一道多项式类计数题。
经典结论:排列排序最少交换次数为 \(n - cnt\),其中 \(cnt\) 是循环个数。
\(k = 0\) 时答案显然为 \(0\);
\(k > 0\) 时,连 \(i \to a_i\),设此时连通块个数为 \(t\),点 \(i\) 入度为 \(d_i\),则最优代价为 \((n-t-\sum_i[d_i = 0]) + k\times\sum_i[d_i = 0]\)。
即把所有入度为 0 的强制接一个入度,并使得最后循环个数尽量多。
由期望线性性质,\(n-(k-1)\times \sum_i[d_i = 0]\) 是很好求的。主要考虑求连通块个数 \(t\)。
设 \(f_i\) 表示 \(i\) 个点的连通图数量,可以通过多项式 \(\ln\) 求出。则一样由期望线性性质得 \(\sum t=\sum f_i\times(n-i)^{n-i}\),卷积即可。
时间复杂度 \(O(n\log n)\)。
1006 Alice and Bob(咕)
博弈不会草只是因为懒而已吧,咕了。
1007 Tree
罚时垫底的原因找到了!
因为想抢首 A 所以莽得太快然后 GG。。。
枚举唯一的度数不受限制的点,发现剩下的是个换根 dp。转移时取相邻点的 dp 值中前 \(\min\{d_i, k - 1\}\) 大的。
每个点的复杂度都是 \(\min\{d_i, k - 1\}\log n\),而 \(\sum d_i = O(n)\),所以总复杂度 \(O(n\log n)\)。
注意特判 \(k = 0\)。
1008 Set2
删了 \(p = \lfloor\frac{n}{k+1}\rfloor\) 次,最后剩 \(r = n\bmod (k + 1)\) 个。
记 \(f_i\) 表示只考虑被删除的数,最后一次删掉的最小为 \(i\) 的方案数,则 \(ans_m = \sum_{i<m}\binom{n-i-1}{r-1}\times f_i\),这部分时间复杂度 \(O(n^2)\)。
记 \(g_{i,j}\) 表示只考虑最后 \(i\) 次被删除的数,最后一次删掉的最小为 \(j\) 的方案数,转移时枚举在 \(j\) 之前的数,用隔板法算转移系数。
注意 \(g\) 的方案数中还要考虑 \(j\) 之后的数的排列顺序,可以转移时乘阶乘逆元,最后再在乘上阶乘得到 \(f\)。
这部分看似 \(O(n^3)\),实则 \(O(n\times k \times \frac{n}{k})=O(n^2)\)。最后除以总方案数即可,总时间复杂度 \(O(n^2)\)。
1009 Paperfolding
假如横折 \(i\) 次,纵折 \(j\) 次,则答案为 \((2^i+1)(2^j+1)\)。求期望时可以二项式定理。
1010 Function
attention:由于我线代没学好,所以下文中可能会出现线代术语使用混乱的情况。
记 \(V = \mathrm{span}\{a_i\}\)(实现时可用线性基 \(b_1, b_2, \dots, b_k\) 表示 \(V\))。
考虑题目给出的对映射 \(\varphi\) 的限制,它等价于 \(\ker \varphi = \mathrm{im} \varphi\)。由同态基本定理可得 \(V/\ker\varphi = \mathrm{im}\varphi\),因此 \(|\ker\varphi|^2=|V|\)。
那么只有当 \(|V|=2^{\dim V}\) 为完全平方数,即 \(\dim V\) 为偶数时才可能有解。
考虑 construct 部分(其实由同态基本定理你也应该大致知道怎么构造了):假设 \(\vec{x}=\sum_{i=1}^{\frac{k}{2}} a_i b_i +\sum_{i=1}^{\frac{k}{2}}c_i b_{\frac{k}{2} + 1}\),则构造 \(\varphi(\vec{x})=\sum_{i=1}^{\frac{k}{2}} c_ib_i\)。
考虑 check 部分:首先判掉不属于 \(\mathrm{span}\{a_i\}\) 的元素后,如果有解,我们可以得到两个线性子空间的线性映射(用线性基维护是否为线性映射)。
设该映射为 \(\phi : U\to W\),首先判 \(\forall x\in W,(x\not\in U)\or(\phi(x) =0)\) 是否成立(因为 \(W\) 是 \(\ker \varphi\) 的一个子空间)。
其次,由于 \(\dim \varphi = \frac{1}{2}\dim V\),所以我们还需要判 \(\dim W \leq \frac{1}{2}\dim V\leq (\dim V-\dim U) + \dim W\) 是否成立。
然后你发现如果上述条件都成立,则一定可以通过增量法构造合法的 \(\varphi\)。
1011 Exam
显然可以 2-sat 判有无解,用线段树优化建图(注意要连正反两条边,否则区间相包含会出问题)。
注意特殊处理端点处的连边,否则可能出现 \(x\to \lnot x\) 的不合法连边。
然后最小时间,只需要从最后完成的任务开始依次尝试赋值 \(0\),如果出现矛盾则当前任务完成时刻即为最小时间。
每个点只会被赋值一次,所以时间复杂度 \(O(n\log n)\)。
1012 Set1
草,队友怎么是找规律过的啊。怎么还写出未定义行为来了啊。
记 \(k = \frac{n - 1}{2}\),则队友找出来的神必规律如下:
看起来可以随便怼个组合意义上去。
1013 An Easy Matrix Problem
注意到 \(Shift(a,x)_i= i - x\bmod n\)。以下默认把查询中的矩阵差分成四块。
对于 first section:观察发现 \(C_{i,j}\) 的值只与 \(i-j\bmod n\) 有关,不妨记 \(C_{i,j}=f_{i-j\bmod n}\),其中 \(f\) 可以用上面的性质处理出来。
则矩阵查询总可以表示成若干 \(c_1\times\sum f_i^t\) 与 \(c_2\times \sum(i\times f_i^t)\) 之和,其中 \(c_1, c_2\) 是个与 \(f\) 无关的常数。
对于 second section:分成三部分,即初始 + 横加 + 纵加。初始矩阵即上面的内容。
由于最初的性质,横加与纵加都可以看成加上某一行/列加上等差数列,树状数组维护即可。
时间复杂度 \(O(n\log n)\)。
contest 6
没有AK,太丢人了。
最后调 1011 没调出来,赛后十几分钟调出来了。草。
感觉错过了唯一一次可以AK多校的机会。
队友们好强啊,我来的时候已经无罚时 AC 5 道题了。然而菜如我只能贡献罚时.jpg。
1001 Road To The 3rd Building
枚举区间长度 \(l\),则每个点的贡献要么是 \(s_i\times a_l\),要么是 \(s_i\times i\times b_l\),其中 \(a_l, b_l\) 是关于 \(l\) 的常数。
1002 Little Rabbit's Equation
模拟。
1003 Borrow
我的做法比较复杂,不过还是列在这里(因为懒得看题解),仅供参考。
设 \(dp(x, y)\) 表示目前 \(a \leq b \leq c\),且 \(c-b=x,b-a=y\) 的期望次数,终止状态即 \((0, 0)\)。
状态合法(即 \((a+b+c)\bmod 3 = 0\))当且仅当 \(x\equiv y\bmod 3\)。列转移式:
可以解得 \(dp(0, y) = \frac{4}{3}y,dp(1,y)=\frac{4}{3}(y-1)+2\)。尝试代入第一条式子发现好像有 \(dp(x,y)=\frac{4}{3}(y-x)+2x\)。
然而,问题在于当 \(y = 0\) 时无法从 \(dp(x-1,y-1)\) 转移过来,所以我们不妨考虑容斥。记 \(g(x,y)=\frac{4}{3}(y-x)+2x\),枚举假设碰到了 \((z,0)\)。
用组合数算出概率(注意我们并不需要保证到 \((z,0)\) 是第一次碰到 \(y=0\)),则它的贡献为 \(g(z-2,1)-g(z,0)+1\),即强行从 \((x-2,1)\) 转移过来。
由于需要枚举来容斥,时间复杂度为 \(O(x+y+z)\)。
1004 Asteroid in Love
面积最大的点肯定在凸包上取,由于出题人不刻意卡,所以你把三个凸包上的点都试一遍就可以过了。
其实我赛场上本来写的是另一个算法(见下),结果 WA 到死,然后尝试写个暴力看一下是不是凸包的问题结果没想到居然AC了。
考虑第一种颜色任意选点(也可以在凸包上取点),第二种颜色在凸包上按顺时针/逆时针依次选点,第三种颜色先分别求出上凸包与下凸包。
由于上凸包/下凸包上的点与前两种颜色选的点之间的叉乘分别是凸的,所以每次往更大/更小的走一定会走到凸壳顶点,即最优决策点。
而第二种颜色是在凸包上依次取点,所以斜率形成常数个单调区间,每个单调区间在第三种颜色上都是均摊 \(O(n)\),总时间复杂度 \(O(n^2)\)。
当然赛后调一调就过了,而且跑得很快(但我总感觉是因为我在凸包上枚举点而凸包不大的缘故)。
1005 Fragrant numbers
设 \(dp(l, r, x) = 0/1\) 表示通过字符串 \(S[l\dots r]\) 是否可以构造出 \(x\)。
通过算小数据可以发现 \(l, r\) 不会很大(15 左右),因此可以 \(O(15^2n^2)\) 处理一下,然后打个表交上去。
1006 A Very Easy Graph Problem
最短路必须尽量让最大边权尽量小(即最小瓶颈路),因此求个最小生成树,算每条边的贡献。
1007 A Very Easy Math Problem
不懂啊,反演套路题有什么好考的。
1008 Yukikaze and Smooth numbers
不懂啊,为什么min-25筛模板题过的队这么少啊。
先 \(O(\frac{n^{\frac{3}{4}}}{\log n})\) 求出 \(k\) 以内的素数个数。考虑怎么算质因子 \(\leq k\) 的个数,发现 min-25 筛第二部分就是在从小到大枚举质因子。
因此限制一下 min-25 筛跑到的质数 \(\leq k\) 即可,时间复杂度是 min-25 的 \(O(n^{1-\omega})\)。
1009 Divisibility
puts(b % x == 1 ? "T" : "F")
1010 Expectation
拆位 + 矩阵树。
1011 Kirakira
今年 WC 的员交课件《球面上的面积并问题》提到的一种处理面积的方法:上边界的积分 - 下边界的积分。
因此对于每条线段求在它上面/下面的点全部不出现的概率。极角排序一下即可,注意判共线的情况,共线只保留长度最长的线段。
所以不要问我为什么1h还调不出来,问就是我不会计算几何。
contest 7
又又又又自闭了。
因为要参加 noi,可能打不了 contest 9 和 contest 10 了(contest 8 也不一定能打)。才不是放生队友。
1001 Animism(咕)
本题由于过于难写,所以目前除了std,没有验题人验过。
1002 Bitwise Xor
可将选择 \(\oplus a\) 或 \(\oplus b\) 改成先 \(\oplus a\) 再选择 \(\oplus a\oplus b\) 或者不操作。
把 \([l, r]\) 的数塞进线性基,并维护对应下标最大的一组基(显然唯一)。询问时从高位开始扫,如果 \(x\) 的第 \(i\) 位与线性基中的第 \(i\) 位对应的 \(p\) 的第 \(i\) 位不一样,则异或上线性基中的第 \(i\) 位。
进一步地,\([l, r]\) 的线性基可以通过保留 \([1,r]\) 的线性基中下标 \(\geq l\) 的位得到,预处理 \([1,r]\) 的线性基即可,求下标最大的一组基直接贪心即可。
时间复杂度看似是 \(O(n\log^2A)\),其实是 \(O(m\log A + q\log A)\)。
1003 Counting
抄自 https://blog.csdn.net/WAautomaton/article/details/107853952 。
考虑 \(A\) 的结构:我们可以按前缀最大值(非严格)将其划分成若干段,则每个段一定是同时放进去的(归并排序的性质)。
如果区分 \(A\) 中每个数字来自于哪个排列,方案数为 \(f_n = \prod_{i=1}^{n}(i^2 + 1)\)。
可以考虑从大到小构造 \(A\),每种数插入时要么作为开头,要么藏在某个来自同一排列且比它大的数的后面。
因为有两个排列,所以同时在开头还有顺序问题,方案数其实是 \((i-1)^2 + 2i + 2 = i^2 + 1\)。
这会算重多少次?
考虑对于某种方案,我们定义 “段集” 是一个段的集合,且两个排列在其中出现的数完全相同。
让某个段集反转(在该集合中交换两个排列的数)则会得到另一个本质相同的方案。因此如果有 \(x\) 个段集就会算重 \(x\) 次。
由于段集的并、交、补、差仍是段集,那么如果令答案的 egf 为 \(G(x)\),则有 \(G^2(x) = \sum \frac{f_n}{n!}x^n\)。
其实可以良定义 “本原段集” 是不可再拆的段集,则所有段集对应本原段集的幂集。
感觉好像析合树中的本原连续段。
然后多项式平方根即可。
1004 Decision
我太菜了,没想出来这道题咋做,我谢罪。
由于 \(X\) 仅由 \(v_1+v_2\) 决定,所以尝试枚举 \(v_1+v_2\) 并计算所有 \(|v_1-v_2|\) 对应的 \(X\)。
建边 \(x\to (ax+c)\bmod m\),倍增即可。
(然而赛场上我尝试去枚举 \(|v_2-v_1|\) 最后推到一半就不想推了)
1005 Expectation
考虑对于每个 \(x_i-x_{i-1}\) 算期望经过次数。
记 \(f_{0/1,i,j}\) 表示左边有 \(i\) 个球,右边有 \(j\) 个球,考虑中间球到相邻的左洞/右洞的段,它期望被经过多少次。
转移枚举哪个球被选中,如果是中间球,再考虑它向左还是向右。
时间复杂度 \(O(n^2 + Tn)\),题解说可以做到 \(O(n\log n)\),感觉很玄妙。
1006 Flower
你一定做过这样一道题:在树上选若干条不交树链,求最大权和。
那么选若干不交最大权和连通块同理,列 \(dp_x\) 表示 x 的子树内选连通块的最大权和,
连通块在最顶端的点处转移,贡献可以用点分树维护,复杂度 \(O(n\log n)\)。
1007 Game
枚举出距离最远的所有点对,如果起点在其中则先手必胜,否则删去这些点,重复该过程;如果最终只剩下一个点,则先手必败。
1008 Heart
考虑每次计算最高位为第 \(i\) 位的状态,使用子集卷积(即枚举集合大小 + fwt),复杂度 \(O(\sum_{i=0}^{20}i^22^i)=O(20^2\times 2^{20})\)。注意 \(b_i\) 可以相同。
1009 Increasing and Decreasing
(神仙队友终于暴露它原题识别机的本性)
只有 \(x+y-1\leq n\) 且 \(xy\geq n\) 时有解(第二个条件来自于 Dilworth 定理)。
通过观察样例我们可以把序列剖成 \(x\) 个下降序列,让后面的下降序列尽可能长即可字典序最小。
1010 Jogging
(神仙队友再一次通过找规律 carry 全队)
如果起点与 \(x = y\) 连通,则概率为 \(0\);否则概率为 (起点度数 + 1) / (总度数 + n)。
可以发现连通块不会很大,所以直接暴搜找出所有点即可。
1011 Kcats
枚举最小值所在位置 \(x\),\(x\) 对应单调栈大小必然为 1,且 \(x\) 之后的单调栈必然包含 \(x\)。
记 \(f_{l, r, d}\) 表示区间 \([l, r]\),单调栈里面必然包含 \(d\) 个元素的方案数。转移时枚举 \(m\),从 \(f_{l,m-1,d}\) 与 \(f_{m+1,r,d+1}\) 转移来即可。
时间复杂度 \(O(n^4)\),不过这个上界非常松,所以记搜轻松跑过。
然后我发现我赛场上根本没算时间复杂度,交上去就过了,也没想那么多 2333。
contest 8
上午打了一场 unr,自闭了。
“即使是求最长路,也是 NP 完全问题啊!出题人怎么能随便找个 NP 完全问题随便找几个图,就把题出出来了呢?”
拿了铜牌滚粗。这样看来大概 noi 只能打铁了。
1001 Auto-correction
处理出最终序列,发现可以 dp + 前缀最小值优化。
1002 Breaking Down News
这,我还以为 9*10^6 必有什么线性做法高论。
对于所有 \(s_i = x\) 的 \(i\) 建单调队列,然后以 \(s\) 为横坐标建线段树。
不要问我赛场怎么写的,反正我写了个不会证复杂度,看起来很假的做法。
1003 Clockwise or Counterclockwise
判一下叉积正负即可。
1004 Discovery of Cycles
用 lct + 滑窗 求一下每个右端点对应的最小左端点。
1005 Easy NPC Problem(咕)
哪有人会拿集训队论文出题的啊。
1006 Fluctuation Limit
每次可行域一定是某个区间,因此直接取区间最左点即可。
1007 Gaming of Co-prime Disallowance
反演求出结束局面取走卡片个数 \(\leq i\) 的概率 \(f_i\)(注意不能算方案数,否则精度有问题)。
则结束局面取走卡片个数 \(=i\) 的概率 \(g_i = f_i - f_{i-1}\),把偶数位的 \(g\) 加起来即可。注意可能所有数都不互质。
1008 Hexagon

1009 Isomorphic Strings
枚举 \(k\),再枚举第一个块的所有循环同构串并求 hash 值,再对后面的块 check,用 unordered_map 即可(也可以模数取小然后开桶)。
时间复杂度因子和级别,能过。
1010 Jumping on a Cactus
本质是偶环仙人掌拓扑序方案数。建圆方树,在圆方树上 dp。
对于圆点,用树拓扑序的方法来转移;对于方点,可以做个区间 dp 来转移。
1011 Kidnapper's Matching Problem
将 \(a, b\) 中的每个数改成能通过线性基异或出来的最大数,这样所有关于线性基同构的就直接相等了,kmp 即可(什么,题目缩写就是正解?)。
1012 Linuber File System
如果不对点 \(x\) 子树加,则 \(x\) 的权值与 \(x\) 的父亲相同。
先对限制离散化得到 \(\{d_i\}\),然后树形 dp,\(f_{i,j}\) 表示子树 \(i\) 取限制 \([d_j,d_{j+1})\) 的最小代价。
contest 9
1001 Tree
最优解一定是叶子指向根,枚举即可。
1002 Absolute Math
记 \(cnt(n)\) 表示 x 的质因子种类数,则 \(f(n) = 2^{cntp(n)}\),因此有 \(f(ni) = \frac{f(n)f(i)}{f(\gcd(n, i))}\)。
不妨记 \(S(n,m)=\sum_{i=1}^{m}f(ni)=\sum_{i=1}^{m}\frac{f(n)f(i)}{f(\gcd(n, i))}\),反演得到 \(S(n,m)=\sum_{d|n} h(d)\times S(d,\lfloor\frac{m}{d}\rfloor)\),其中 \(h\) 可以预处理。
如果直接递归做,可以通过一些优化擦着时限过。
不过考虑 \(m\leq 10^7\),其实在第二层的 \(S(i,j)\) 已有 \(ij\leq 10^7\),也就是说只有 \(O(10^7\log 10^7)\) 种合法状态,离线处理即可。
1003 Slime and Stones
必败态一定形如 \((\lfloor\frac{1}{2}m(1-k+\sqrt{k^2+2k+5}),\frac{1}{2}m(3+k+\sqrt{k^2+2k+5}\rfloor),m\in \N\)。
至于为什么,可以去查一下 Wythoff 博弈与 Betty 定理。
1004 Product(咕)
随机乘上一些小数逆元然后质因子分解,分解的时候可以玄学剪剪枝啥的 不过听说要调参就不想写。
说到随机化,我就想起了今年的 unr,然后陷入了自闭。
1005 Resistance
思考一下这个电阻咋算,发现可以环与环之间串联,于是可以每个环算贡献,优化一下就线性了。
然后不加 fread 好像会 TLE,可能是我常数太大。
1006 Skyscrapers(咕)
搜索题,跳了跳了。
1007 Game
平衡树维护一下。
1008 Distance(咕)
时 代 的 眼 泪。
二次离线莫队,修改即点到根每个点加上父边长度,查询即点到根求和,树分块可以做到 \(O(\sqrt{n}) - O(1)\),总时间复杂度 \(O(n\sqrt{n})\)。
1009 Yajilin
插头 dp 模板题。好像最小表示法要 TLE,用括号表示法可以过。可能是我常数太大。
1010 Jump(咕)
时 代 的 眼 泪 * 2。
如果是链,则路径长度最小 = 路径边数最小,因此区间减 + 区间 min 即可。
考虑选出一个关键点集合,关键点下面的每次暴力跳,并用若干棵线段树维护每个关键点到根的链。
如果每次剥去叶子,剥了 \(B\) 次,则剩下的叶子有 \(O(\frac{n}{B})\) 个。选择这些叶子为关键点可做到 \(O(nB + \frac{n^2}{B}\log n)\),平衡一下得 \(O(n\sqrt{n\log n})\)。
然而并不想写 2333。
contest 10
1001 Anti-hash Test(咕)
大概就是当 \(n\) 比较小时暴力,当 \(n\) 比较大时找出 \(s(n)\) 的后缀自动机的规律。
不过由于我太懒,所以不想写这道题。
1002 Network Test
没看懂 tutorial,于是自己瞎写了一个做法:
首先瞎猜结论,大概就是求所有非空诱导子图的 \(\lceil\frac{m}{n-1}\rceil\) 的最大值。然后你发现如果已知 \(k = \lceil\frac{m}{n-1}\rceil\) 则类似于最大权闭合子图,不过要求必须是非空子图。
(update 2020/09/07:这个结论可以通过拟阵并证明,可以看 2018 的论文)
枚举在集合内的点,增量法求一求当前最大的 \(k\),然后就没有任何理论依据地过了。
1003 Mine Sweeper
对于 \(S \leq 25\),可以构造 \(1\times c\) 的矩阵形如 \(.X.X.X.X\)。
对于 \(S>25\),令 \(S=8x+3y\),则随意选 \(x\) 个不相邻格子,再在角落堆 \(y\) 个格子即可。
(由于我队友告诉我的构造方法太复杂,所以就写了题解的构造方法)
1004 Permutation Counting
「LibreOJ NOI Round #2」不等关系 的弱化版,直接 \(O(n^2)\) 就可以过了。
1005 Tree Cutting
枚举直径中心(奇数为边,偶数为点),代价即与中心距离 \(>\frac{k}{2}\) 的点数。
这个显然可以点分治,不过也显然可以长链剖分(类似于「十二省联考 2019」希望 的处理即可)。
1006 Divide and Conquer(咕)
先随便找一条直线平分点集,第二条直线可以二分斜率,定位出对应斜率平分点集的直线,根据某侧的点数来调整二分。最后还有微调使得有整点落在上面。
因为不想写所以咕掉了。
1007 Coin Game
将每个物品等价拆解成 \((a_i, 1)\) 与 \((a_i+b_i, 2)\),排序后按奇偶性分类贪心取即可。
1008 I do not know Graph Theory!
强连通分解后,如果原图有多个强连通分量,则由第一个指向最后一个的边翻转才合法。
否则,对强连通竞赛图求哈密顿回路,回路外的边翻转显然合法。
回路上的边可以瞎维护一通,反正可以 \(O(n^2)\) 求出所有回路上的边翻转是否合法。
(因为忘了怎么强连通竞赛图求哈密顿回路所以调了半天没调出来的 zz)
1009 Photography
数学必修四习题(确信)。
由于平行直线答案一样,不妨选取直线 \((0,0)+t\times(\cos\theta,\sin\theta)(t\in R)\)。
记 \(p_i = (x_i,y_i)\cdot(\cos\theta,\sin\theta)=x_i\cos\theta + y_i\sin\theta\),则 \(d_{i,j}^2 = (p_i - p_j)^2\)。
将 \(\sum_{i}\sum_{j} d_{i,j}^2\) 拆一拆得到式子 \(A\sin^2\theta+B\sin\theta\cos\theta+C\cos^2\theta\),倍角 + 辅助角求最值即可。动态修改时可以快速维护出 \(A, B, C\) 的值。
1010 Tic-Tac-Toe-Nim
如果先手取空了一堆石子导致某行/某列出现了两堆空,则后手再取空另一堆即胜利,故这些石子不能被取空。
枚举前两次取的结果,将那些不能被取空的减一,然后转化成了 nim 游戏。
1011 Task Scheduler
结论:当 \(k = 0\) 时按编号排;否则按 \(t\) 降序排列,编号为第二关键字。
证明:读者自证不难,留作习题,答案略。
尝试交换论证,假设 \(t_i > t_{i+1}\)。不妨记 \(m' = m-\sum_{j<i} t_j\),并记 \(a_j = \frac{m'-j}{m'-j-k}\),则:
当 \(k = 0\) 时,前后因式同时恒为零;否则同时恒为正。


