@hdu - 5960@ Subsequence
@description@
给定如下计算序列权值的函数:

对于一个由三元组 (cost0, cost1, color) 组成的序列 A,求通过以上函数计算出来的第 k 大的子序列的权值。
Input
第一行一个整数 t,表示数据组数。
对于每组数据,第一行包含两个整数 n, k。
接下来 n 行,每行三个整数 cost0, cost1, color (0 <= cost0, cost1<= 10000;0 <=color <=1),第 i 行描述 A 的第 i 个三元组。
保证至少有 k 个非空子序列。单组数据中 n <= 50000。∑n <= 400000,∑k <= 400000。
Output
对于每一行,输出对应的答案。
Sample Input
1
3 4
2 1 0
1 3 1
3 1 1
Sample Output
3
Hint
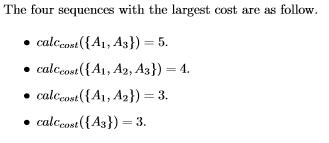
@solution@
大多数的 k 大问题都可以对应转化成 k 短路的模型,只是有些只能用 k 短路的思想来做而不能直接写裸 k 短路。
k 短路怎么做呢?在技术不发达的时代可以用 A* 玄学搜索,但现在发达了,于是我们有了效率更高的做法。
假如我们要求 s 到 t 的 k 短路,我们可以先求出在反向图中以 t 为根的最短路树(即每个点到 t 的最短路径构成的树)。
于是这样,s 到 t 的每一条路径将会经过一些树边与非树边。我们不妨用路径经过的非树边序列表示这样一条路径。
接下来,我们用优先队列存储当前的非树边序列。每一次选出最小的序列并进行拓展。
对于一个非树边序列,每一次拓展,要么在序列最末加入一条非树边,要么替换掉序列最后的非树边。
那么拓展 k 次后就可以得到我们的 k 短路。
最短路肯定就是 s 到 t 的纯树边道路(即非树边序列为空),我们将其加入初始优先队列。
怎么实现呢?我们先对于每条非树边 u -> v : w 算出 -dis[u] + w + dis[v],即选择这条非树边会增加的代价,记为它的权值。
然后用可持久化可并堆,得到 x 到 t 的树边路径上所有点连出去的非树边构成的堆。
于是在最末加入一条新的非树边就很好操作了:取出最末非树边 (u, v) 的 v 对应的那个堆的堆顶。
那么怎么进行替换呢?我们在每个优先队列的结点中再存储一个可持久化可并堆,表示可用决策。
每次进行替换时,将可并堆的堆顶删除得到新的可用决策。
OK。我们来看这道题怎么转成 k 短路。
其实很简单,我们建 2*(n+2) 个点,第 i 对点表示 cur = 0 与 cur = 1 两种状态。
其中第 0 对(中 cur = 0 的那个点)表示源点,第 n + 1 对表示汇点。
然后对应在 i-1 与 i 之间连一连就好啦。
@accepted code@
#include<queue>
#include<vector>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define fi first
#define se second
#define mp make_pair
#define rep(G, x) for(Graph::edge *p = G.adj[x];p;p = p->nxt)
typedef pair<int, int> pii;
typedef long long ll;
const int MAXN = 50000;
struct Heap{
struct node{
node *ch[2];
int dis, key, num;
}pl[100*MAXN + 5], *ncnt, *NIL;
Heap() {
NIL = &pl[0];
NIL->ch[0] = NIL->ch[1] = NIL;
NIL->key = NIL->dis = 0;
}
node *newnode(int k, int p) {
ncnt++;
ncnt->ch[0] = ncnt->ch[1] = NIL;
ncnt->key = k, ncnt->num = p, ncnt->dis = 1;
return ncnt;
}
node *newnode(node *x) {
ncnt++; *ncnt = *x;
return ncnt;
}
void pushup(node *x) {
if( x->ch[1]->dis > x->ch[0]->dis )
swap(x->ch[0], x->ch[1]);
x->dis = x->ch[1]->dis + 1;
}
node *merge(node *x, node *y) {
if( x == NIL ) return y;
if( y == NIL ) return x;
if( x->key < y->key ) swap(x, y);
node *p = newnode(x);
p->ch[1] = merge(x->ch[1], y);
pushup(p); return p;
}
void clear() {ncnt = &pl[0];}
node *insert(node *x, int k, int p) {return merge(x, newnode(k, p));}
node *erase(node *x) {return merge(x->ch[0], x->ch[1]);}
}T;
struct node{
int x, k, dis; Heap::node *rt;
node(int _x=0, int _k=0, int _d=0, Heap::node *_rt=T.NIL):x(_x), k(_k), dis(_d), rt(_rt) {}
friend bool operator < (const node a, const node b) {
return a.dis < b.dis;
}
};
struct Graph{
struct edge{
int to, dis, id;
edge *nxt;
}edges[4*MAXN + 5], *adj[2*MAXN + 5], *ecnt;
void addedge(int u, int v, int w, int id) {
edge *p = (++ecnt);
p->to = v, p->dis = w, p->id = id;
p->nxt = adj[u], adj[u] = p;
}
void clear(int n) {
for(int i=1;i<=n;i++) adj[i] = NULL;
ecnt = &edges[0];
}
}G1, G2;
int ecnt;
void addedge(int u, int v, int w) {
ecnt++, G1.addedge(u, v, w, ecnt), G2.addedge(v, u, w, ecnt);
}
Heap::node *rt[2*MAXN + 5];
int pre[2*MAXN + 5], dis[2*MAXN + 5], ind[2*MAXN + 5];
void topo(int s, int t) {
for(int i=s;i<=t;i++)
rep(G2, i) ind[p->to]++;
queue<int>que;
for(int i=s;i<=t;i++) {
if( ind[i] == 0 ) que.push(i);
pre[i] = dis[i] = -1;
}
dis[t] = 0, rt[t] = T.NIL;
while( !que.empty() ) {
int f = que.front(); que.pop();
rep(G2, f) {
int t = p->to, id = p->id;
if( dis[f] + p->dis > dis[t] ) {
dis[t] = dis[f] + p->dis;
pre[t] = id;
}
ind[t]--;
if( ind[t] == 0 ) {
rt[t] = T.NIL;
rep(G1, t) {
if( p->id == pre[t] )
rt[t] = T.merge(rt[t], rt[p->to]);
else rt[t] = T.insert(rt[t], dis[p->to] - dis[t] + p->dis, p->to);
}
que.push(t);
}
}
}
}
int get_kth(int s, int t, int k) {
topo(s, t);
priority_queue<node>que;
que.push(node(s, dis[s], dis[s], T.NIL));
for(int i=1;i<=k;i++) {
node t = que.top(); que.pop();
if( i == k ) return t.dis;
if( t.rt != T.NIL )
que.push(node(t.rt->num, t.k, t.k + t.rt->key, T.erase(t.rt)));
if( rt[t.x] != T.NIL )
que.push(node(rt[t.x]->num, t.dis, t.dis + rt[t.x]->key, T.erase(rt[t.x])));
}
return -1;
}
int cost[2][MAXN + 5], clr[MAXN + 5], id[2][MAXN + 5];
void solve() {
T.clear(); int n, k, cnt = 0;
scanf("%d%d", &n, &k);
for(int i=0;i<=n;i++)
id[0][i] = (++cnt), id[1][i] = (++cnt);
int s = id[0][0], t = ++cnt;
G1.clear(t), G2.clear(t), ecnt = 0;
for(int i=1;i<=n;i++) {
scanf("%d%d%d", &cost[0][i], &cost[1][i], &clr[i]);
for(int j=0;j<2;j++)
addedge(id[j][i-1], id[j][i], 0), addedge(id[j][i-1], id[clr[i]][i], cost[j][i]);
}
addedge(id[0][n], t, 0), addedge(id[1][n], t, 0);
printf("%d\n", get_kth(s, t, k));
}
int main() {
int T; scanf("%d", &T);
while( T-- ) solve();
}
@details@
我一开始写的是带标记的可持久化堆(也就是没有建图跑 k 短路这么简单粗暴的方法):维护两个堆 A, B 分别表示 cur = 0 与 cur = 1 的情况,每次要么往 A, B 中插入元素,要么 A, B 同时加上一个权值。
然后就被卡空间了。可喜可贺,可喜可贺。


