@codeforces - 1214H@ Tiles Placement
@description@
给定一个 n 点的树,一条简单路径的长度为这条路径所含点的个数。
现给每个点涂色,颜色编号为 1~k。要求每一条长度恰为 k 的简单路径上点的颜色互不相同。
请构造一个方案,或者判定无解。
Input
第一行两个整数 n,k (2≤k≤n≤200000),表示点的个数与颜色个数。
接下来 n-1 行,每行两个整数 vi 和 ui (1≤vi,ui≤n),描述了每条边。
保证是一棵树。
Output
如果无解输出 "No"。
否则输出 "Yes",接下来输出 n 个数表示每个点的颜色。
Examples
Input
7 4
1 3
2 3
3 4
4 5
5 6
5 7
Output
Yes
1 1 2 3 4 1 1
Input
7 3
1 3
2 3
3 4
4 5
5 6
5 7
Output
No
Note
第一个样例方案如下:

@solution@
@part - 1@
首先看一种特殊情况:一条链。
显然我们可以从链的前面往后依次涂 1, 2, ..., k, 1, 2, ...,这个方案是一定合法的。
并且可以注意到,其他方案总可以等价地转成这个方案(相同的颜色依然相同)。
再来看一种特殊情况:k = 2。
实际上就是二分图染色,不难发现这个情况也是一定合法。
如果无解,至少要满足 k > 2,且有一个点是三叉的。

如图,a, b, c 是三条不相交的链。
如果满足 a + b >= k,b + c >= k,c + a >= k 则无解(这里的长度为点的数量)。
至于怎么证,不妨假设 a >= b >= c,则一定有 a >= k/2。
则一定可以 a 选出长度 p,b 选出长度 q,c 选出长度 r 使得 p + q = p + r = k,且 p >= k/2;q, r < k/2。
又因为 b + c >=k,所以 q 段与 r 段一定可以在同一个长度为 k 的段里面。又因为 q, r 的颜色集合相同,于是矛盾。
注意要特判 k = 2,这个证明对 k = 2 不成立。
其实当 a >= b >= c 时,只需要保证 b + c >= k 就肯定无解了。
@part - 2@
然后开始我们的构造。
首先取出这棵树的直径,按照链的方法给这个直径涂色。
因为直径的性质,所有点一定距离直径的某一个端点最远,因此我们只需要找出次远和第三远就可以判断无解了。
从直径的某个端点开始 dfs。对于直径外的点,父亲的那条边连向直径,次远和第三远一定在它的子树中产生。
而对于直径上的点,次远和第三远还可能连向直径的另一个端点,需要另行判断。
假如以上无解判断完成后,我们以直径的中间边为界,开始往两边 dfs,相同深度的涂相同颜色。
然后就构造完成了。没错,这样一定是一个合法的方案。
可以反证,假如存在一个不合法的路径。考虑以下三种可能的位置情况:
(1)与直径不相交:
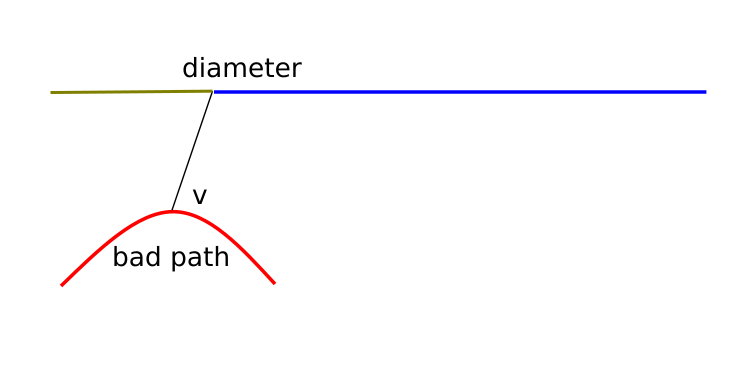
这种情况上面早就判掉了。
(2)与直径有交,但不经过直径中心边:
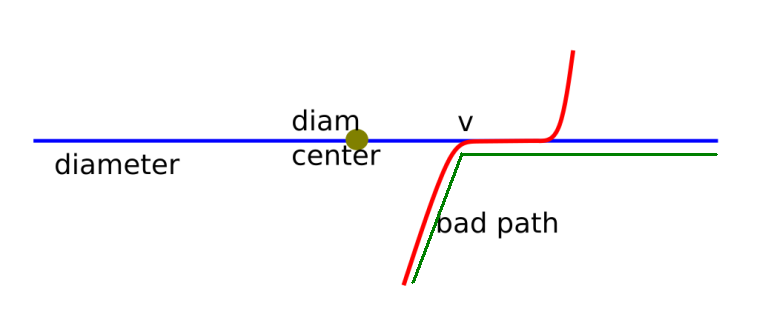
根据直径的定义,红色肯定没有绿色长,而假如绿色长度 >= k 上面也已经判掉了。
(3)与直径有交且直径中心边:

这个时候的确有可能长度 >= k,但是按照上面的构造方法,这种情况一定不会出现相同的颜色。
@accepted code@
#include<cstdio>
#include<cstdlib>
const int MAXN = 200000;
struct edge{
int to; edge *nxt;
}edges[2*MAXN + 5], *adj[MAXN + 5], *ecnt = &edges[0];
int clr[MAXN + 5], n, k;
void addedge(int u, int v) {
edge *p = (++ecnt);
p->to = v, p->nxt = adj[u], adj[u] = p;
p = (++ecnt);
p->to = u, p->nxt = adj[v], adj[v] = p;
}
int dep[MAXN + 5];
void dfs1(int x, int f) {
dep[x] = dep[f] + 1;
for(edge *p=adj[x];p;p=p->nxt)
if( p->to != f ) dfs1(p->to, x);
}
int get_pos(int x) {
dfs1(x, 0); int mx = x;
for(int i=1;i<=n;i++)
if( dep[i] > dep[mx] ) mx = i;
return mx;
}
bool tag[MAXN + 5];
void dfs2(int x, int f) {
for(edge *p=adj[x];p;p=p->nxt)
if( p->to != f ) {
dfs2(p->to, x);
tag[x] |= tag[p->to];
}
}
int f[MAXN + 5], g[MAXN + 5];
int nxt(int x) {return (x == k) ? 1 : x + 1;}
int lst(int x) {return (x == 1) ? k : x - 1;}
void dfs4(int x, int fa, int type) {
if( type ) clr[x] = nxt(clr[fa]);
else clr[x] = lst(clr[fa]);
for(edge *p=adj[x];p;p=p->nxt)
if( p->to != fa ) {
dfs4(p->to, x, type);
if( f[p->to] + 1 > f[x] )
g[x] = f[x], f[x] = f[p->to] + 1;
else if( f[p->to] + 1 > g[x] )
g[x] = f[p->to] + 1;
}
if( f[x] && g[x] && f[x] + g[x] + 1 >= k ) {
puts("No");
exit(0);
}
}
int mxdep;
void dfs3(int x, int fa) {
clr[x] = nxt(clr[fa]); f[x] = g[x] = 0;
for(edge *p=adj[x];p;p=p->nxt)
if( p->to != fa ) {
if( tag[p->to] ) dfs3(p->to, x);
else {
if( dep[x] <= mxdep - dep[x] + 1 )
dfs4(p->to, x, 0);
else dfs4(p->to, x, 1);
if( f[p->to] + 1 > f[x] )
g[x] = f[x], f[x] = f[p->to] + 1;
else if( f[p->to] + 1 > g[x] )
g[x] = f[p->to] + 1;
}
}
if( f[x] && g[x] && f[x] + g[x] + 1 >= k ) {
puts("No");
exit(0);
}
if( f[x] && f[x] + dep[x] >= k && f[x] + mxdep - dep[x] + 1 >= k ) {
puts("No");
exit(0);
}
}
int main() {
scanf("%d%d", &n, &k);
for(int i=1;i<n;i++) {
int u, v; scanf("%d%d", &u, &v);
addedge(u, v);
}
if( k == 2 ) {
puts("Yes"), get_pos(1);
for(int i=1;i<=n;i++)
printf("%d ", (dep[i] & 1) + 1);
return 0;
}
int p = get_pos(1), q = get_pos(p); mxdep = dep[q];
tag[q] = true, dfs2(p, 0), clr[0] = k, dfs3(p, 0);
puts("Yes");
for(int i=1;i<=n;i++)
printf("%d ", clr[i]);
puts("");
}
@details@
因为没特判 k = 2,狠狠地 WA 了一发。


