@hdu - 5293@ Tree chain problem
@description@
给定 n 个点的树,以及 m 条带权的树链。
选出一些没有公共点的树链,使得选出的树链权值和最大。
Input
第一行给定数据组数 T (T<=10)。
对于每组数据,第一行两个整数 n, m (1<=n,m<=100000)。
接下来 n - 1 行每行两个整数 ai, bi,描述一条边 (ai, bi) (1≤ai,bi≤n)。
接下来 m 行每行三个整数 u, v 与 val(1≤u,v≤n,0<val<1000)描述一条链的端点 u, v 以及链的权值。
Output
对于每组数据,输出最大权值和。
Sample Input
1
7 3
1 2
1 3
2 4
2 5
3 6
3 7
2 3 4
4 5 3
6 7 3
Sample Output
6
@solution@
首先对于每条链,我们仅在链的最高点(即 lca(u, v))处考虑它的贡献。
由此,考虑使用 dp。定义 dp[x] 表示从 x 的子树中选取得到的最大权值和。
考虑转移。首先如果不选经过 x 的链,则 dp[x] 为所有儿子的 dp 之和。
如果选取一条(显然只能选取一条)经过 x 的链。如图,假如我们选中紫色的链,则我们需要把绿点的 dp 求和。
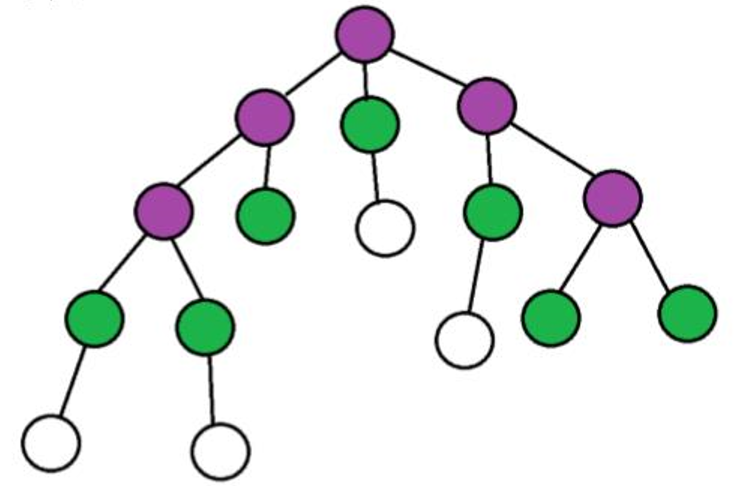
(P.S:这张图是我从课件上扒下来的,不是我画的)
暴力遍历整条链肯定行不通,考虑使用数据结构来维护。
我们对于每个点 i 给定点权为 ∑dp[j] - dp[i],其中 j 是 i 的儿子。则只需要求链上除 lca 的点的点权和 + lca 的儿子 dp 值之和。
相当于我们需要一个支持单点修改 + 链求和的数据结构。用树链剖分 + 线段树或者 dfs 序 + 线段树/树状数组即可。
@accepted code@
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN = 100000;
struct Line{
int u, v, val;
Line(int _u=0, int _v=0, int _val=0):u(_u), v(_v), val(_val) {}
};
vector<Line>vec[MAXN + 5];
struct Graph{
struct edge{
int to; edge *nxt;
}edges[2*MAXN + 5], *adj[MAXN + 5], *ecnt;
void init(int n) {
for(int i=1;i<=n;i++)
adj[i] = NULL;
ecnt = &edges[0];
}
void addedge(int u, int v) {
edge *p = (++ecnt);
p->to = v, p->nxt = adj[u], adj[u] = p;
p = (++ecnt);
p->to = u, p->nxt = adj[v], adj[v] = p;
}
}G;
struct Segtree{
struct node{
int l, r, s;
}t[4*MAXN + 5];
void build(int x, int l, int r) {
t[x].l = l, t[x].r = r, t[x].s = 0;
if( l == r ) return ;
int mid = (l + r) >> 1;
build(x << 1, l, mid), build(x << 1 | 1, mid + 1, r);
}
void pushup(int x) {
t[x].s = t[x<<1].s + t[x<<1|1].s;
}
void modify(int x, int p, int k) {
if( p > t[x].r || p < t[x].l )
return ;
if( t[x].l == t[x].r ) {
t[x].s = k;
return ;
}
modify(x << 1, p, k), modify(x << 1 | 1, p, k);
pushup(x);
}
int query(int x, int l, int r) {
if( l > t[x].r || r < t[x].l )
return 0;
if( l <= t[x].l && t[x].r <= r )
return t[x].s;
return query(x << 1, l, r) + query(x << 1 | 1, l, r);
}
};
struct TreeDivide{
Segtree T;
int siz[MAXN + 5], dep[MAXN + 5], hvy[MAXN + 5], fa[MAXN + 5];
void dfs1(const Graph &G, int x, int f) {
siz[x] = 1, dep[x] = dep[f] + 1, fa[x] = f, hvy[x] = 0;
for(Graph::edge *p=G.adj[x];p;p=p->nxt) {
if( p->to == f ) continue;
dfs1(G, p->to, x);
siz[x] += siz[p->to];
if( siz[p->to] > siz[hvy[x]] )
hvy[x] = p->to;
}
}
int dfn[MAXN + 5], tid[MAXN + 5], top[MAXN + 5], dcnt;
void dfs2(const Graph &G, int x, int tp) {
dfn[++dcnt] = x, tid[x] = dcnt, top[x] = tp;
if( hvy[x] ) dfs2(G, hvy[x], tp);
for(Graph::edge *p=G.adj[x];p;p=p->nxt) {
if( p->to == fa[x] || p->to == hvy[x] ) continue;
dfs2(G, p->to, p->to);
}
}
void build(const Graph &G) {
dcnt = 0, dfs1(G, 1, 0), dfs2(G, 1, 1);
T.build(1, 1, dcnt);
}
int lca(int u, int v) {
while( top[u] != top[v] ) {
if( dep[top[u]] < dep[top[v]] ) swap(u, v);
u = fa[top[u]];
}
if( dep[u] < dep[v] ) swap(u, v);
return v;
}
void modify(int x, int k) {
T.modify(1, tid[x], k);
}
int query(int x, int y) {
int ret = 0;
while( top[x] != top[y] ) {
ret += T.query(1, tid[top[y]], tid[y]);
y = fa[top[y]];
}
return ret + T.query(1, tid[x], tid[y]);
}
}T;
int dp[MAXN + 5], sum[MAXN + 5], n, m;
void dfs(int x, int f) {
sum[x] = 0;
for(Graph::edge *p=G.adj[x];p;p=p->nxt)
if( p->to != f )
dfs(p->to, x), sum[x] += dp[p->to];
dp[x] = sum[x]; T.modify(x, sum[x]);
for(int i=0;i<vec[x].size();i++) {
int tmp = T.query(x, vec[x][i].u) + T.query(x, vec[x][i].v) - sum[x];
dp[x] = max(dp[x], tmp + vec[x][i].val);
}
T.modify(x, sum[x] - dp[x]);
}
void init(int n) {
G.init(n);
for(int i=1;i<=n;i++)
vec[i].clear();
}
void solve() {
scanf("%d%d", &n, &m); init(n);
for(int i=1;i<n;i++) {
int a, b; scanf("%d%d", &a, &b);
G.addedge(a, b);
}
T.build(G);
for(int i=1;i<=m;i++) {
int u, v, val; scanf("%d%d%d", &u, &v, &val);
vec[T.lca(u, v)].push_back(Line(u, v, val));
}
dfs(1, 0);
printf("%d\n", dp[1]);
}
int main() {
int T; scanf("%d", &T);
while( T-- ) solve();
}
@details@
只是因为太久没写过树链剖分回来练习练习而已。。。
而且这道题树链剖分也不会被卡满 log^2,所以也不需要什么区间加区间求和的树状数组。


