@hdu - 6057@ Kanade's convolution
@description@
给定序列 A[0..2^m-1] 与 B[0..2^m-1] ，求：
输出 \(\sum_{i=0}^{2^m-1}C[i]*1526^i \mod 998244353\)
input
第一行包含一个整数 m。
第二行包含 2^m 个整数 A[0..2^m-1]。
第三行包含 2^m 个整数 B[0..2^m-1]。
output
输出一个整数表示答案。
sample input
2
1 2 3 4
5 6 7 8
sample output
568535691
@solution@
先冷静地打表观察：
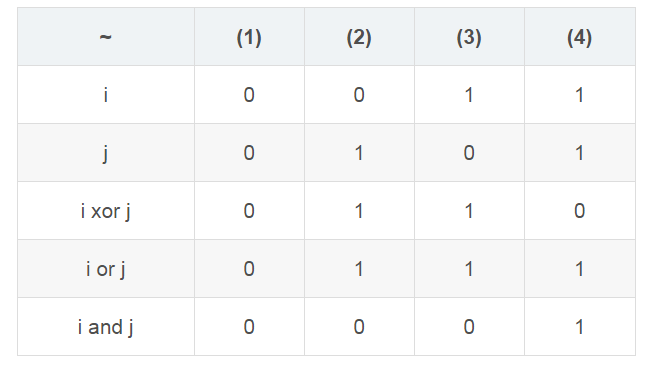
好的这道题所需要的所有结论都在上面了。
令 a = i xor j, b = i or j, c = i and j。
当我们确定 a, b 过后，有多少对 (i, j) 可以得到 a, b 呢？当 异或 和 或 某一位都等于 0 时，两个皆为 0；当 异或 为 0 而 或 为 1 时，两个皆为 1；否则就会产生两种情况。
令 bits(x) 表示 x 的二进制表示中 1 的个数，整理一下上面的结论，一共有 2^bits(a) 种不同的 (i, j) 可以相应地得到 a, b。
所以我们一开始给 A[x] 乘上 bits(x)，就可以直接考虑 a, b, c 之间的关系而不用管 i, j。
仔细观察有 a ^ b = c。
但是这样就没了吗？我们发现，当 a = 1 的时候，b 不可能为 0。也就说，这是一个比异或卷积约束性更强的卷积。它还要求 a&b = a。
用我们刚刚引入的 bits 这一概念，约束可以转换为 bits(b) - bits(a) = bits(c)。这个应该是显然成立的。
因此我们可以将 A 数组里 bits = i 的所有数放到一个数组 P[i][...] 里面去，B 数组里 bits = j 的所有数放到一个数组 Q[j][...] 里面去，这样将 P[i] 与 Q[j] 作普通的异或卷积得到 R[j-i]，最后再将 R[j-i] 中 bits = j-i 的保留下来。
通过预先进行 FWT 可以做到总时间复杂度 \(O(m^2\log m)\)。
@accepted code@
#include<cstdio>
typedef long long ll;
const int MOD = 998244353;
const int INV2 = (MOD + 1)>>1;
const int MAXM = 19;
const int MAXN = 1<<19;
void fwt(ll *a, int n, int type) {
for(int s=2;s<=n;s<<=1)
for(int i=0,t=(s>>1);i<n;i+=s)
for(int j=0;j<t;j++) {
ll x = a[i+j], y = a[i+j+t];
a[i+j] = (x + y)*(type == 1 ? 1 : INV2)%MOD;
a[i+j+t] = (x - y)*(type == 1 ? 1 : INV2)%MOD;
}
}
int bits[MAXN + 5]; ll pw[MAXN + 5];
int lowbit(int x) {
return x & -x;
}
int read() {
int x = 0; char ch = getchar();
while( ch > '9' || ch < '0' ) ch = getchar();
while( '0' <= ch && ch <= '9' ) x = 10*x + ch-'0', ch = getchar();
return x;
}
ll a[MAXM + 5][MAXN + 5], b[MAXM + 5][MAXN + 5], c[MAXM + 5][MAXN + 5];
int main() {
int m, n; pw[0] = 1;
scanf("%d", &m); n = (1<<m);
for(int i=1;i<n;i++) {
pw[i] = pw[i^lowbit(i)]<<1;
bits[i] = bits[i^lowbit(i)] + 1;
}
for(int i=0;i<n;i++)
a[bits[i]][i] = pw[i]*read()%MOD;
for(int i=0;i<n;i++)
b[bits[i]][i] = read();
for(int i=0;i<=m;i++)
fwt(a[i], n, 1), fwt(b[i], n, 1);
for(int i=0;i<=m;i++)
for(int j=0;j<=i;j++)
for(int k=0;k<n;k++)
c[i-j][k] = (c[i-j][k] + a[j][k]*b[i][k])%MOD;
for(int i=0;i<=m;i++)
fwt(c[i], n, -1);
ll ans = 0, tmp = 1;
for(int i=0;i<n;i++,tmp=tmp*1526%MOD)
ans = (ans + c[bits[i]][i]*tmp)%MOD;
printf("%lld\n", (ans%MOD + MOD)%MOD);
}
@details@
一般来说，要求数 i 与数 j 在做异或卷积的同时还要满足其他约束（比如 i & j = i 或是 i & j = 0 之类的），可以通过枚举二进制位中 1 的个数进行求解。
