@总结 - 6@ 后缀自动机
@0 - 参考资料@
@0.5 - 引言@
后缀自动机(Suffix Automaton,简称 SAM)概念比较抽象,构造方法比较抽象,复杂度证明也比较抽象。所以对于初学者体验感极差是很正常的。
但是关键是,这个东西应用倒是很广泛。
@1 - what is it?@
@自动机@
自动机嘛,就是扔进去一个字符串,判断它是否具有某个特征,具有返回 true,不具有返回 false。
我们所说的后缀自动机就是用来判断某一个字符串是否为给定的串 S (称为母串)的后缀。
@DAWG@
你可以把后缀自动机看成一个有向无环图。具体来讲是这样的:
这个图有一个起点(初始状态),同时每条转移边上有一个字符。
从起点出发到达某一结点的一条路径对应着一个字符串(即将路径上所有转移边的字符依次连起来),我们称这个结点表示这一个字符串。显然一个结点可以表示多个字符串。
假如某结点表示的所有字符串都是母串的后缀,我们就标记这个结点。被标记的结点集合称为结束状态集合。
对于某一个字符串 T,我们从起点出发,在第 i 次沿着 Ti 这条边走,最终走到的终点如果被标记了,就返回 true(称 T 被自动机识别)。
我们称这个有向无环图为 DAWG。
对于某一个字符串,比如 “aabbabd”,很容易想到一个非常简单暴力的 DAWG 构造方法(结束状态集合为叶子结点集合):
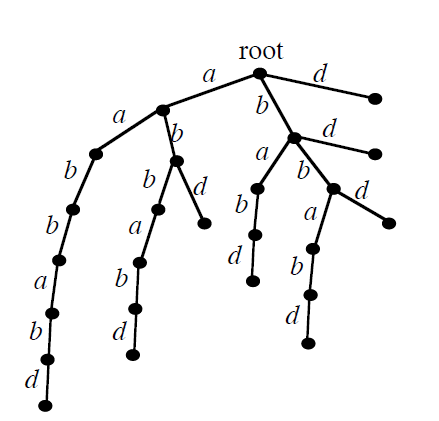
【图片取自陈立杰的课件】【好像从 root 出发的 “bbd” 所对应的叶子节点是不需要的?还是我理解有误?】
然而这样点数为 O(n^2) 的。我们考虑简化这个自动机。
假如我们已经识别了“abb”,接下来如果想要识别成功,则我们必须要经过 'a', 'b', 'd' 三条边。
假如我们已经识别了“bb”,接下来如果想要识别成功,则我们也必须要经过 'a', 'b', 'd' 三条边。
两者是一样的,所以我们完全可以将两个结点合为一个结点。
更进一步的,我们想要知道怎样的结点可以合为一个结点。
@终点集合 end-pos@
为了统一,以下字符串的下标从 0 开始。
定义(1):我们定义字符串 T 的终点集合 end-pos(T),为 T 在母串 S 中所有出现位置的右端点构成集合(因为是右端点,课件中又称为 right(T))。
例如对于母串 S=“aabbabd”:end-pos(“a”) = {0, 1, 4},end-pos(“ab”) = {2, 5},end-pos(“abba”) = 4。
当后缀自动机中的某两个结点的 end-pos 相同时,在它后面加字符(相当于访问它的出边)也是相同的,所以它们的出边集合相同,就可以将它们合并为同一个结点。
当一个后缀自动机上不存在 end-pos 相同的结点时,则称这个是最简状态后缀自动机。
这里有一些性质:
性质(1):如果 end-pos(T1) = end-pos(T2),则要么 T1 是 T2 的后缀,要么 T2 是 T1 的后缀。
这个证明比较显然,因为 T1 和 T2 的右端点相同。
性质(2):end-pos(T1) 与 end-pos(T2) 如果有交集,则其中一个是另一个的子集。
如果有交集,则说明某一个地方 T1 与 T2 有相同的右端点,故其中一个是另一个的后缀。
性质(3):end-pos 相同的所有字符串,长度一定构成连续的区间。
这个说起来有点麻烦,还是举个例子解释一下:
对于母串 S=“aabbabd”,end-pos(“bb”) = end-pos(“abb”) = end-pos(“aabb”) = 3。这些串的长度分别为 2, 3, 4,构成了连续区间 [2, 4]。
证明可以利用性质(1),(2),反证一下。此处不再赘述。
定义(2):我们称一个结点 s 能够表示的最长字符串长度为 max(s),结点 s 能够表示的最短字符串长度为 min(s)。则根据最简后缀自动机的定义与性质(3),结点 s 能够表示 min(s) ~ max(s) 内的所有结点,且这些结点呈后缀关系。
比如对于刚刚那个例子,max(s) = 4,min(s) = 2。
@后缀链接 与 parent 树@
为了线性构造后缀自动机,我们还需要一些东西。
定义(3):若对于结点 s,结点 t 表示的所有字符串是结点 s 表示的所有字符串的后缀,且 min(s) = max(t) + 1,则 s 向 t 连一条单向的虚边,称为后缀链接。记 t = fa(s)。
同时可以发现结点 t 还满足 end-pos(s) \(\subset\) end-pos(t)。
还是举例子:假如结点 s 能表示的字符串为 {aabba, abba, bba},则结点 t 可以是 {ba, a}。
定义(4):根据我们刚刚的性质(2),后缀链接一定构成了一棵树,我们称为 parent 树。其中 parent 树的根是 DAWG 的起点。
网上把 parent 树 也叫作 前缀树,不过考虑到大家如果看到在众多后缀中突然出了一个前缀可能有些懵,所以这里就写的不是前缀树。事实上,前缀树这个名字也有它的道理,此处不展开。
@2 - how to build it?@
@理论@
【建议在理解了上面说的这些东西过后再来看这一小节,不然你就会像我初学的时候一样晕乎乎的】
接下来我们就来讲讲怎么去构造这样一个后缀自动机。
我们采用的基本方法为增量法进行在线构造,即每次在母串后面加入一个新的字符并维护当前的后缀自动机。
令原母串 S 的后缀自动机中,能够表示整个母串 S 的结点为 lst。则 lst 到树根的路径上的结点 lst, fa(lst), fa(fa(lst)), ..., root 包含了 S 的所有后缀。
考虑对 S + c 建立后缀自动机,这个新串会增加 |S| + 1 个子串。我们需要让 DAWG 识别这些新子串。我们新建一个结点 cur 表示这些新串。
可以发现这些新子串等于原来的后缀 + 字符 c。所以我们仅对 lst, fa(lst), fa(fa(lst)), ..., root 进行操作。令 v1 = lst, v2 = fa(lst), ..., vk = root。
分两类情况讨论:
(1)假如 v1...k 都没有字符 c 这条转移边,则我们直接把 v1...k 向 cur 连字符 c 的转移边,并将 cur 的后缀链接连向 root。
(2)假如 vi 是第一个有字符 c 这条转移边的,设 vi 通过字符 c 连向 p。可以根据我们上面的性质证明 vi 之后的所有结点一定有字符 c 这条转移边。我们把 vi 之前的结点向 cur 连字符 c 的转移边,这样子 DAWG 的性质就满足了(可以识别这些新串)。我们再设法去满足 parent 树的性质:
【接下来的内容就是最让我自闭的内容了】
我们找到 vj,使得 vj 是最后一个通过字符 c 这条转移边到达 p 的结点,则有 min(vj) + 1 = min(p)。
又因为 i 到 p 存在一条转移边,所以有 max(p) >= max(vi) + 1。
当 max(p) = max(vi) + 1 时,此时 p 所表示的所有字符串都是通过 vi...j 转移过来的,因此都是 cur 的后缀,所以直接 cur 向 p 连后缀链接。
当 max(p) > max(vi) + 1 时,我们新建一个结点 np 使得 max(np) = max(vi) + 1,并将 min(p) 修改为 max(np) + 1。我们想要通过改变一些边使得 np 与修改后的 p 所能表示的字符串并集等于修改前的 p 所能表示的字符串。
将 vi...j 原本连向 p 的边改为向 np 连边,并将 p 的后缀链接连向 np,再将 cur 的后缀链接连向 np 即可。这样修改过后, parent 树的性质也可以满足了。
@代码@
实际实现中我们可以不存储 min(s),因为 min(s) = max(fa(s)) + 1。
下面这份代码只是展现构造后缀自动机的过程,并无实际作用。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 1000000;
struct node{
node *ch[26], *fa; int mx;
}pl[2*MAXN + 5], *tcnt, *root, *lst;
void init() {
lst = tcnt = root = &pl[0];
for(int i=0;i<26;i++)
root->ch[i] = NULL;
root->fa = NULL, root->mx = 0;
}
node *newnode() {
tcnt++;
for(int i=0;i<26;i++)
tcnt->ch[i] = NULL;
tcnt->fa = NULL, tcnt->mx = 0;
return tcnt;
}
void sam_extend(int x) {
node *cur = newnode(), *p = lst;
cur->mx = lst->mx + 1; lst = cur;
while( p != NULL && p->ch[x] == NULL )
p->ch[x] = cur, p = p->fa;
if( p == NULL )
cur->fa = root;
else {
node *q = p->ch[x];
if( q->mx == p->mx + 1 )
cur->fa = q;
else {
node *cne = newnode();
(*cne) = (*q); cne->mx = p->mx + 1;
cur->fa = q->fa = cne;
while( p != NULL && p->ch[x] == q )
p->ch[x] = cne, p = p->fa;
}
}
}
char s[MAXN + 5];
int main() {
init(); scanf("%s", s);
int len = strlen(s);
for(int i=0;i<len;i++)
sam_extend(s[i] - 'a');
}
@证明@
结点数量 O(n):
每一次只会增加 1 ~ 2 个结点,故结点数量是 O(n) 的。
转移边数量 O(n):
我们对所有转移边求一个生成树。任意的生成树皆可。
显然树边是 O(n) 的。
对于非树边 u -> v,我们找一条由三部分组成的路径:
(1)从起点开始经过树边到达 u。
(2)u -> v
(3)从点 v 开始经过字典序最小的转移边(非树边或树边皆可)到达一个可接受的结点。根据我们后缀自动机的性质,这条路径一定是存在的。
这个路径对应着一个后缀。故我们每一条非树边都对应一个后缀。
我们将每个后缀对应路径上第一条非树边。故每个后缀最多对应一条非树边。
所以非树边数量 <= 后缀数量 = n。
所以转移边数量是 O(n) 的。
算法本身的时间复杂度 O(n):
因为我们结点数量和转移边数量是 O(n) 的,其他地方是 O(n) 的比较显然,可能最不容易分析时间复杂度的地方是将 vi...j 向 np 连边这一部分的时间复杂度。
因为 max(np) = max(i) + 1, min(np) = min(j) + 1,所以我们发现这样连边最多只会改变 min(i) - min(j) 条边(对我没有写错的确是 min(i) 而不是 max(i))。同时注意到 min(j) <= min(i) <= min(fa(lst)) , min(fa(cur)) = min(np) = min(j) + 1。
以上说明了什么呢?在我们建构后缀自动机时,min(fa(lst)) 最多只会增加 1,且如果我们多连一条边, min(fa(lst)) 就会严格减少。
这样就是 O(n) 的了。
@3 - where can it use?@
upd in 2019/01/11:写了一些题,大致来讲讲后缀自动机的一些基础用法吧。
主要是利用 “子串总是某个后缀的前缀” 这一性质,通过后缀自动机进行子串操作与信息统计。
@LCS@
最长公共子串(longest common substring)的缩写。
最基本当然是两个串之间的 LCS 啦。这里有一道模板题。
可以发现这个东西也可以用于字符串匹配(就是 kmp 干的事情),当最长公共子串就是模式串时匹配成功。
当然也有扩展版本:多个串求 LCS。类似的思想(即对某一个串建后缀自动机,用其他串来打标记)也可以用来多个串求一些奇怪的特有子串。
注意在这个时候需要沿着 fa 边传一些奇怪的信息(类 AC 自动机)。
@K-th 子串@
求某个串的字典序第 K 小的子串。这里是一道模板题。
这利用了 DAWG 是一个 DAG 的性质,在 DAWG 跑 dp 等在有向无环图上可以实现的算法。
还有一些利用字典序的贪心思想在里面。
同时,后缀自动机还可以通过求字典序最小的子串来求解循环移位找字典序最小的表示这一问题。这里有一道这样的题。
好像以前都是用什么最小表示法来做。
@子串出现次数@
很经典的一类问题。主要是利用了 end-pos 这一集合的性质。
我们把每次通过增量法加入的结点当作有效结点,可以通过在 parent 树内的子树中有效结点的信息和来求得某一结点 end-pos 集合的信息。这里有一道模板题。
当然,说起树这种我们最熟悉不过的东西,我们还有很多花样可以玩。
@广义后缀自动机@
科学点说,这个后缀自动机就是 “trie 的后缀自动机”。可以把它理解 kmp 和 AC 自动机之间的联系。
其实就是对多个串建同一个后缀自动机。
在代码实现上,就是如果要加入新的字符串,就将 last 指针重新移回 root。
如果某个转移边以前出现过会怎样?你会发现新加入的点并不会与其他点连通,因为它不会和它之前的任何结点连边。
所以并不会有什么特别复杂的实现。只是概念上的一个突破而已。
update in 2019/08/14:然而。。。上面那个真的只是“对多个串建后缀自动机”。。。
如果是 trie 树上建后缀自动机,需要使用 bfs 构造,每次某个结点的 last 指针重定位到它父亲对应的后缀自动机中的结点。
具体的题。。。emmm 我暂时还没找到。。。再慢慢找吧。。。
@与后缀树的联系@
事实上后缀自动机,后缀数组与后缀树之间有很深的联系。
不过后缀自动机与后缀树联系更紧密一些,因为——
我们后缀自动机的 parent 树其实就是翻转过后的后缀树。
所以你会发现,后缀自动机可以替代后缀树的所有功能并还能实现其他功能。
不知道高到哪里去了。但是这带给我们一个启示,有时候可能需要翻转原串建后缀自动机(其实本质上还是建后缀树,只是少搞点概念比较好)。
所以如果你再看我所提到的前缀树这一概念,其实就是从这里得到的名字。


