@loj - 2483@「CEOI2017」Building Bridges
@desription@
有 n 根柱子依次排列,第 i 根柱子的高度为 hi 。现可以花费 (hi - hj)^2 的代价建桥架在第 i 根柱子和第 j 根柱子之间。
所有用不到的柱子都会被拆除,第 i 根柱子被拆除的代价为 wi 。
求用桥把第 1 根柱子和第 n 根柱子连接的最小代价。注意桥梁不能在端点以外的任何地方相交。
input
第一行一个正整数 n。 2 <= n <= 10^5。
第二行 n 个空格隔开的整数,依次表示 h1, h2, ..., hn。0 <= hi <= 10^6。
第三行 n 个空格隔开的整数,依次表示 w1, w2, ..., wn。0 <= |wi| <= 10^6。
output
输出一个整数表示最小代价,注意最小代价不一定是正数。
sample input
6
3 8 7 1 6 6
0 -1 9 1 2 0
sample output
17
@solution@
一个很 naive 的 dp:定义状态 \(dp[i]\) 表示将 1 与 i 连接起来的最小费用,并再定义一个前缀和 \(s[i] = \sum_{p=1}^{i}w[p]\),则状态转移为:
update in 2019/11/12 : 抱歉我现在才发现我的 dp 转移式写错了。。。应该为 s[i-1] 而非 s[i],第 i 根柱子不能拆。
满脸的斜率优化。
横坐标为 \(x[j] = h[j]\),纵坐标为\(y[j] = dp[j] - s[j] + h[j]^2\),斜率为 \(k[i] = 2*h[i]\),只和 i 有关的常数 \(c[i] = s[i-1] + h[i]^2\)。
转移式变为:
然而……斜率不单调就算了……TM 横坐标也不单调。
对于这种题,一是写平衡树,一是用 cdq 分治。
因为我这辈子都不会去写平衡树维护斜率的 cdq 分治非常的优秀,所以我就在这里讲一下 cdq。
感性描述一下我们的思想:我们把区间分为两部分,左半部分依照横坐标排序,右半部分依照斜率排序,同时保证左半部分所有的编号小于右半部分所有的编号。
在这个前提下,用左边去更新右边,就是一个简单的单调栈问题了。
我们当然不可能在每一层都去排一下序什么的,这样时间复杂度就退化成 O(nlog^2n) 的。
所以我们的解决方法是这样的:
首先我们把所有点按照斜率来排序,开始递归区间 [1, n]。
对于当前这一层 [l, r],将这些点按照编号与 mid 的关系,分成左右两部分,同时两部分内部都保持斜率单调的顺序。因为我们一开始递归的是 [1, n],按照上面这一套方法,递归 [l, r] 的时候这个区间内所有点的编号都在 [l, r] 范围内。
然后,先递归 [l, mid],求出这段区间的 dp 值,并在递归时以它们的横坐标为关键字进行排序(归并排序)。
再一套单调栈更新右半部分。递归 [mid, r] 求解。此时左右两部分都是以横坐标为关键字的有序状态。
在最后归并即可。
好像有些冗长……最好看一看代码确认一下细节。
@accepted code@
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 100000;
const ll INF = (1LL<<62);
struct node{
ll w, h, c, k, x, y, dp;
int pos;
}a[MAXN + 5], tmp[MAXN + 5], que[MAXN + 5];
bool cmp(node a, node b) {
return a.k < b.k;
}
void cdq(int le, int ri) {
if( le == ri ) {
a[le].x = a[le].h;
a[le].y = a[le].h*a[le].h + a[le].dp - a[le].w;
return ;
}
int mid = (le + ri) >> 1, p = le, q = mid + 1, r = le;
for(r = le;r <= ri;r++)
if( a[r].pos <= mid ) tmp[p++] = a[r];
else tmp[q++] = a[r];
for(r = le;r <= ri;r++)
a[r] = tmp[r];
cdq(le, mid);
int s = 1, t = 0;
for(p = le;p <= mid;p++) {
while( s < t && (que[t].y - que[t-1].y)*(a[p].x - que[t].x) >= (a[p].y - que[t].y)*(que[t].x - que[t-1].x) )
t--;
que[++t] = a[p];
}
for(q = mid + 1;q <= ri;q++) {
while( s < t && a[q].k*(que[s+1].x - que[s].x) >= (que[s+1].y - que[s].y) )
s++;
a[q].dp = min(a[q].dp, a[q].c + que[s].y - que[s].x*a[q].k);
}
cdq(mid + 1, ri);
p = le, q = mid + 1, r = le;
while( p <= mid && q <= ri ) {
if( a[p].x == a[q].x )
tmp[r++] = (a[p].y < a[q].y) ? a[p++] : a[q++];
else tmp[r++] = (a[p].x < a[q].x) ? a[p++] : a[q++];
}
while( p <= mid )
tmp[r++] = a[p++];
while( q <= ri )
tmp[r++] = a[q++];
for(r = le;r <= ri;r++)
a[r] = tmp[r];
}
int main() {
int n; scanf("%d", &n);
for(int i=1;i<=n;i++)
scanf("%lld", &a[i].h), a[i].pos = i;
for(int i=1;i<=n;i++)
scanf("%lld", &a[i].w), a[i].w += a[i-1].w;
for(int i=1;i<=n;i++)
a[i].k = 2*a[i].h, a[i].c = a[i].h*a[i].h + a[i-1].w, a[i].dp = INF;
a[1].dp = 0;
sort(a+1, a+n+1, cmp); cdq(1, n);
for(int i=1;i<=n;i++)
if( a[i].pos == n ) printf("%lld\n", a[i].dp);
}
@details@
cdq 分治真的太巧妙了。
我们需要维护三部分的有序性:斜率,横坐标,编号。
你看 cdq 分治,只需要一点点离线化,就可以顺利解决这三部分的矛盾。
巧妙,太巧妙了。
@another solution@
关于转移式:
如果令 \(b(j) = dp[j] + h[j]^2 - s[j], k(j) = -2*h[j], x(i) = h[i], c(i) = s[i-1] + h[i]^2\),还可以将其写作:
可以看成每次插入一条直线 y = k(j) * x + b(j),对于给定 x(i) 求所有直线在 x(i) 这个位置取到的最小值。
这是一个李超线段树的模板题。直接上李超线段树就好了。
关于李超线段树是什么,网上有详细的教程。在这里附上 yyb 大佬的 blog。
感性地说明一下。我们线段树的每一个结点维护一条直线。
插入的时候会出现一个区间出现两条直线的情况,此时如果一条直线在此区间内比另一条直线高,则可以删去高的那一条直线。
否则会出现相交,如下:
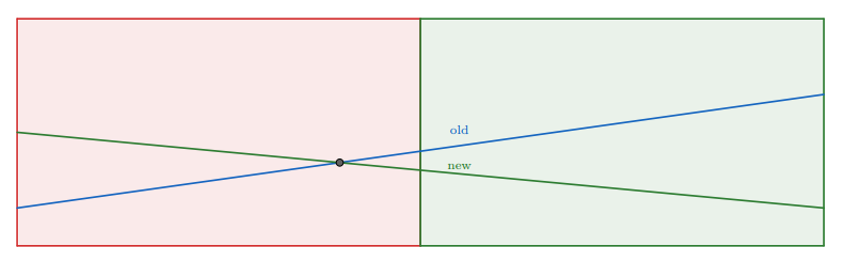
此时发现保留下面的折线最优。
注意到当保留下面的折线时 old 这一条的右边部分不见了,所以我们就用 new 替换 old,并把 old 往左半部分插入。
其他情况也是类似的,比如交点在右边之类的。
插入时是一条路往下走,所以复杂度为线段树的深度 O(log)。
查询时直接在线段树中往下找,统计沿途的直线的 min,也是 O(log)。
有人说这个是标记永久化的一种体现。但其实我也不是很懂,感觉这个线段树充满了人类智慧。
这个方法的优势在于它是在线的。
至于它和上面那些维护凸包的方法(平衡树,cdq 分治)的联系,李超线段树好就好在,解决了维护凸包不能快速插入点的问题(至于删除还是不大行)。而且这玩意儿还可以可持久化(毕竟线段树嘛)。
维护凸包的优势。。。更直观?不是很清楚。做的题目太少了。
@another code@
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
#define lch (x<<1)
#define rch (x<<1|1)
const int MAXN = 100000;
const int MAXH = 1000000;
struct line{
ll k, b;
line(ll _k=0, ll _b=0) : k(_k), b(_b) {}
ll get(ll x) {return k * x + b;}
}t[4*MAXH + 5];
ll dp[MAXN + 5], h[MAXN + 5], s[MAXN + 5];
void build(int x, int l, int r) {
int mid = (l + r) >> 1;
t[x].k = -2 * h[1], t[x].b = h[1] * h[1] - s[1];
if( l == r ) return ;
build(lch, l, mid), build(rch, mid + 1, r);
}
void insert(int x, int l, int r, line ln) {
int m = (l + r) >> 1;
ll l1 = t[x].get(l), l2 = ln.get(l);
if( l2 < l1 ) swap(l1, l2), swap(ln, t[x]);
ll m1 = t[x].get(m), m2 = ln.get(m);
ll r1 = t[x].get(m), r2 = ln.get(r);
if( m1 > m2 ) {//注意不能取等于,不然会无限递归
swap(ln, t[x]);
insert(lch, l, m, ln);
}
else if( r1 > r2 )//同上,不能取等于
insert(rch, m + 1, r, ln);
}
ll query(int x, int l, int r, ll p) {
if( l == r ) return t[x].get(p);
int mid = (l + r) >> 1;
if( p <= mid ) return min(query(lch, l, mid, p), t[x].get(p));
else return min(query(rch, mid + 1, r, p), t[x].get(p));
}
int main() {
int n; scanf("%d", &n);
for(int i=1;i<=n;i++) scanf("%lld", &h[i]);
for(int i=1;i<=n;i++) scanf("%lld", &s[i]), s[i] += s[i-1];
build(1, 1, MAXH);
for(int i=1;i<=n;i++) {
if( i == 1 ) dp[i] = 0;
else dp[i] = s[i-1] + h[i]*h[i] + query(1, 1, MAXH, h[i]);
insert(1, 1, MAXH, line(-2*h[i], dp[i] + h[i]*h[i] - s[i]));
}
printf("%lld\n", dp[n]);
}


