@NOIP2018 - D1T3@ 赛道修建
@题目描述@
C 城将要举办一系列的赛车比赛。在比赛前,需要在城内修建 m 条赛道。
C 城一共有 n 个路口,这些路口编号为 1,2,…,n,有 n−1 条适合于修建赛道的双向通行的道路,每条道路连接着两个路口。其中,第 i 条道路连接的两个路口编号为 ai 和 bi,该道路的长度为 li 。借助这 n-1 条道路,从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路 e1,e2,…,ek,满足可以从某个路口出发,依次经过 道路 e1,e2,…,ek(每条道路经过一次,不允许调头)到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全,要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案,使得修建的 m 条赛道中长度最小的赛道长度最大(即 m 条赛道中最短赛道的长度尽可能大)
输入
输入文件第一行包含两个由空格分隔的正整数 n,m,分别表示路口数及需要修建的赛道数。
接下来 n-1 行,第 i 行包含三个正整数 ai,bi,li,表示第 i 条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 n-1 条道路相互到达。每行中相邻两数之间均由一个空格分隔。
输出
输出共一行,包含一个整数,表示长度最小的赛道长度的最大值。
输入样例#1
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7
输出样例#1
31
输入样例#2
9 3
1 2 6
2 3 3
3 4 5
4 5 10
6 2 4
7 2 9
8 4 7
9 4 4
输出样例#2
15
输入输出样例 1 说明
所有路口及适合于修建赛道的道路如下图所示: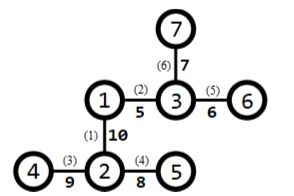
道路旁括号内的数字表示道路的编号,非括号内的数字表示道路长度。 需要修建 1 条赛道。可以修建经过第 3,1,2,6 条道路的赛道(从路口 4 到路口 7), 则该赛道的长度为 9 + 10 + 5 + 7 = 31,为所有方案中的最大值。
输入输出样例 2 说明
所有路口及适合于修建赛道的道路如下图所示:
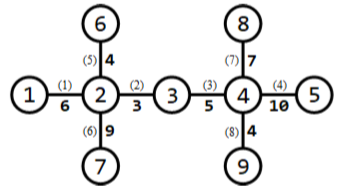
需要修建 3 条赛道。可以修建如下 3 条赛道:
经过第 1,6 条道路的赛道(从路口 1 到路口 7),长度为 6 + 9 = 15;
经过第 5,2,3,8 条道路的赛道(从路口 6 到路口 9),长度为 4 + 3 + 5 + 4 = 16;
经过第 7,4 条道路的赛道(从路口 8 到路口 5),长度为 7 + 10 = 17。
长度最小的赛道长度为 15,为所有方案中的最大值。
数据规模与约定
对于所有的数据, 2 ≤ n ≤ 50,000,1 ≤ m ≤ n-1,1 ≤ ai,bi ≤ n,1 ≤ li ≤ 10,000。
@题解@
首先:看到“使得最小值最大”,一定要联想到二分答案。
考虑已经固定了最小长度 ≥ x 过后我们应该怎么求解链的最大个数。
令 f(u) 表示以 u 为根的子树剖分成长度 ≥ x 的最多的链个数。再令 g(u) 表示满足 f(u) 最大的情况下,从 u 的某个子孙到达 u 的最长链的长度。
为什么要先满足 f(u) 最大呢?假如牺牲 f(u) 使得 g(u) 变大,则 g(u) 对总答案的贡献最多为 1。假如 f(u) 减少 1,总答案不变;否则总答案还要变小。
怎么求解这两个值呢?对于某一个 u,实际上就是相当于这样一个问题:
给你若干数,让你两两配对,使得满足两个数之和 ≥ x 的配对数尽量多。
这里的若干个数就是 g(u的儿子) + u到该儿子的边长。
这个问题又怎么做呢?因为我们既要求解出 f 的最大值,但也要最大化 g。所以我们尽量先配对掉数值小的。
考虑那个最小的数:如果最大的数不能和这个最小的数配对,就直接更新 g(u) 然后跳过;否则求出能和这个最小的数配对的数 p,删掉 p(视为它已经和最小数匹配),然后 f(u)++。
注意我们还要处理:如果某一个数已经 ≥ x 了,就直接 f(u)++,并删除这个数。
为什么这样是对的呢?如果链(a, b)是由链(a, c) + 链(c, b)组成,且链(a, c)的长度已经 ≥ x。则:如果我们把链(a, b)替换成链(a, c) + 链(c, b),答案不会变小。
@代码@
删除这个操作我是使用的并查集来做的。
代码实现的细节可能比较多……?大家如果看不懂可以留言在下面问我 qwq 。
对了,代码因为是在考场上写的,所以代码中的变量可能和上面所说的不大一样,还请大家见谅。
#include<cstdio>
#include<algorithm>
using namespace std;
const int MAXN = 50000;
const int INF = int(1E9);
struct edge{
int to, len;
edge *nxt;
}edges[2*MAXN + 5], *adj[MAXN + 5], *ecnt=&edges[0];
void addedge(int u, int v, int w) {
edge *p = (++ecnt);
p->to = v, p->len = w;
p->nxt = adj[u], adj[u] = p;
p = (++ecnt);
p->to = u, p->len = w;
p->nxt = adj[v], adj[v] = p;
}
int cnt, fa[MAXN + 5], tot[MAXN + 5];
int mid, f[MAXN + 5], g[MAXN + 5];
int find(int x) {
return fa[x] = (fa[x] == x) ? x : find(fa[x]);
}
void solve(int x) {
sort(f+1, f+cnt+1);
for(int i=1;i<=cnt+1;i++)
fa[i] = i;
for(int i=cnt;i>=1;i--)
if( f[i] >= mid )
fa[i] = i+1, tot[x]++;
int pos = cnt;
for(int i=1;i<=cnt;i++) {
if( fa[i] != i ) continue;
while( pos > 0 && f[pos] + f[i] >= mid )
pos--;
pos = max(pos, i);
int p = find(pos+1);
if( p == cnt+1 )
g[x] = max(g[x], f[i]);
else fa[p] = p+1, tot[x]++;
}
}
void dfs(int rt, int pre) {
tot[rt] = 0; g[rt] = 0;
for(edge *p=adj[rt];p!=NULL;p=p->nxt) {
if( p->to == pre ) continue;
dfs(p->to, rt); tot[rt] += tot[p->to];
}
cnt = 0;
for(edge *p=adj[rt];p!=NULL;p=p->nxt) {
if( p->to == pre ) continue;
f[++cnt] = g[p->to] + p->len;
}
solve(rt);
}
bool check(int m) {
dfs(1, 0);
return tot[1] >= m;
}
int main() {
int n, m, le = INF, ri = 0;
scanf("%d%d", &n, &m);
for(int i=1;i<n;i++) {
int a, b, l;
scanf("%d%d%d", &a, &b, &l);
addedge(a, b, l); ri += l; le = min(le, l);
}
while( le < ri ) {
mid = (le + ri + 1) >> 1;
if( check(m) ) le = mid;
else ri = mid - 1;
}
printf("%d\n", le);
return 0;
}


