CodeForces 1110G. Tree-Tac-Toe
题目简述:给定$n$个节点的树,其中一些节点被染成了白色(其余节点未染色)。黑白双方博弈,白先动。轮到黑(白)方时,选择树上的一个未染色的节点并将其染成黑(白)色。率先达成三连色(即存在三个节点$a, b, c$,其中$a$与$b$相连,$b$与$c$相连,且他们的颜色相同)的一方获胜。问哪方获胜或者和局。
解:code
观察1:任何一个游戏开始之前被染成白色的节点$A$,可以等价于添加边$(A, B), (B, C), (B, D)$,并把$A$设为未染色,其中$B, C, D$是新添加的节点(并且只在此处出现)。(见下图,来自 CodeForces)
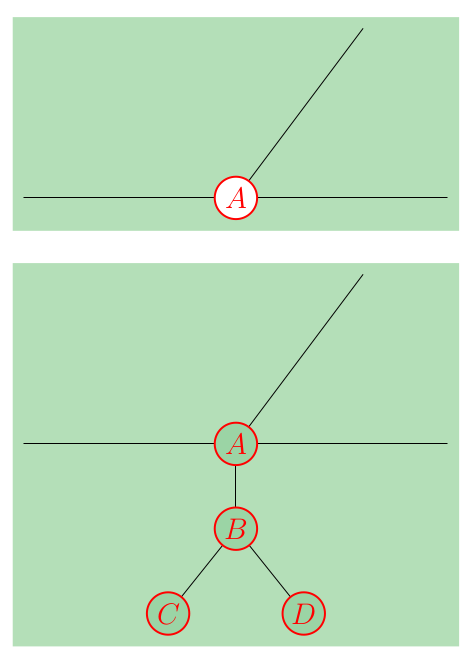
证明:白方先动,则选择节点$A$染色,这样黑方只能选择节点$B$染色,不然白方将$B$染色后必胜——这就相当于节点$A$在游戏开始之前被染成白色;白方不可能先染节点$B, C, D$,这样节点$A$可被黑方染色,显然局势劣于白方选择先染节点$A$。
通过观察1,我们可以将$n$个节点的树转化成一个至多$4n$个节点、并且每个节点都未染色的树,我们将这样的树称为【标准的】。
观察2:若存在一个节点,其度数$\geq 4$,则白方必胜。(见下图,来自 CodeForces)
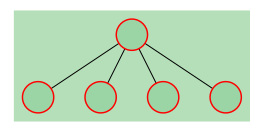
证明:白方直接选择度数$\geq 4$的节点染色,则显然必胜。
观察3:若存在一个节点度数$ = 3$,且这个节点有至少$2$个相邻节点的度数$\geq 2$,则白方必胜。(见下图,来自 CodeForces)
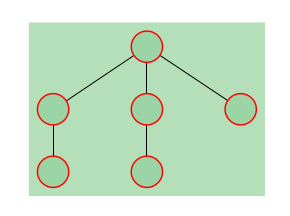
证明:白方直接选择图3中的根节点染色,则显然必胜。
观察3.1:若存在$\geq 3$个度数$=3$的节点,则其中必存在一个度数$=3$的节点至少有$2$个度数$\geq 2$的相邻节点,从而转化为观察3的情形。
观察4:若树中只有$2$个度数$=3$的节点,且这两个节点的距离为偶数,则白方必胜。(见下图,来自 CodeForces)
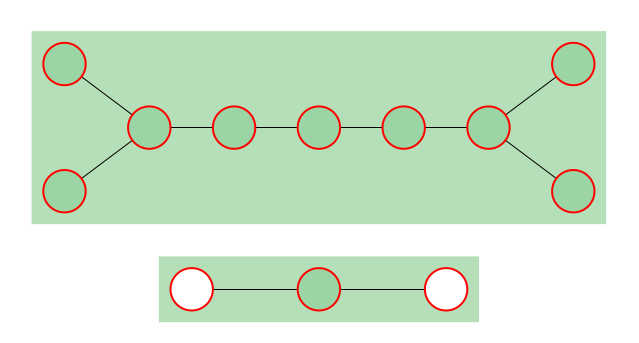
证明:考虑两个度数$=3$的节点对应的树链。若这两个节点的距离$\geq 4$,则根据观察1,我们课可以将其化为左右两端节点染成白色的一条链上的问题,显然白方必胜;若距离$=2$,白方也显然必胜。
观察5:在【标准的】树中,白方必胜当且仅当这棵树能满足观察2至观察4中所述情况,除了这些情况外,一定和局。
观察2至观察4的条件均可在$O(n)$时间内检验,故时间复杂度为$O(n)$。



