数据结构-静态查找表

 

 

 

一、  查找概念

假设有两组数据:

int array1[]={6,4,5,3,8,7,1,2,0,9};

int array2[]={0,1,2,3,4,5,6,7,8,9};

一个有序数组,一个无序数组, 在他们之间查找某一个值的方法有什么区别呢,

对于两组数据我们都可以用最直接的方法，逐个比较直到遇到合适的值。

思路是怎么样的呢:从表中最后一个记录开始，逐个进行记录的关键字和给定值的比较，若某个记录的关键字和给定值比较相等，则返回返回记录所在的位置，或查找完所有记录后还没有发现符合的记录，则查找失败。我们称其为顺序查找。

当数据是一个有序的情况时，我们可以利用这样一种思路：当记录的key按关系有序时可以使用折半查找

对于给定key值，逐步确定待查记录所在区间，每次将搜索空间减少一半（折半）， 直到查找成功或失败为止。我们称其为折半查找。

若要利用计算机帮助我们实现查找的过程，就需要我们了解查找的相关知识.

查找：查询(Searching)特定元素是否在表中。

查找表：由同一类型的数据元素（或记录）构成的集合。

查找成功：若表中存在特定元素，称查找成功，应输出该记录；

查找失败：否则，称查找不成功（也应输出失败标志或失败位置）。

静态查找表：只查找，不改变集合内的数据元素。

动态查找表：既查找，又改变（增减）集合内的数据元素。

关键字：记录中某个数据项的值，可用来识别一个记录。

主关键字：可以唯一标识一个记录的关键字。例如：学号

次关键字：识别若干记录的关键字。例如：女

二、  顺序表查找

   顺序查找（ Linear search，又称线性查找 ）用逐一比较的办法顺序查找关键字，这显然是最直接的办法。

1. 1.        顺序表查找算法

顺序查找算法：

int Search_Seq( int  *a , int n，int  key )
{
for( i=1；i<=n;  i++)
{
            if(key==a[i])
{
                return i;
}
}
      return 0;
} 

这里元素都放在数组下标为1的地方开始，返回0意味着查找失败，比较的时候只要注意key的数据类型就可以了。

1. 1.        顺序表查找优化//比较次数减少

改进后的顺序查找算法

int Search_Seq( int  *a , int n，int  key )
{
     int i=n;     //指向表尾部
     a[0]=key;   //把待查记录放在a[0]中做监视哨
while（a[i]!=key）
{
   i--;
}
return i;    /*返回0 意味着失败*/
} 

这里免去数组越界的判断，从末端开始查找，当数据记录较多的时候能够大大的提高效率，可以注意这种编程技巧。

1.        顺序查找的平均查找长度

 

顺序查找平均查找长度（ASL  Average Search Length），假设查找的表中有n个元素，查找每个元素的概率相等，那么查找第一个元素的次数是1次，查找第二个元素的次数是2次，以此类推查找第n个元素的次数是n次。则总的查找次数为：1+2+3+...+n。这是一个等差数列，求得和后为（1+n）*n/2;再由于n种情况的概率一样，则平均起来计算为

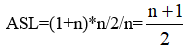
因此得到顺序查找的平均查找长度的结论是： (n+1)/2。

一、  有序表查找

1. 1.        折半查找

折半查找前提是顺序存储，记录有序。

思想：与记录中间值比较，如果比中间值小去左边查，否则去右边查找，直到找到为止，区域内没记录时查找失败。

算法：

int Binary_Search( int  *a , int n，int  key )
{
     int low,high,mid;
     low=1;
     high=n;
while（low<=high）
{
        mid=(low+high)/2;   //定位中间的记录 
        if(key<a[mid])
            high=mid-1;    //小于中间记录high移到mid左边即mid-1
else if(key>a[mid])
            low=mid+1;    //大于中间记录high移到mid右边即mid+1
else
        return mid;
}
return 0;    /*返回0 意味着失败*/
}

这两种查找方式的主要区别：

 

1. 2.        折半查找的平均查找长度

折半查找的平均查找长度分析：由于折半查找算法的特点，没次会抛弃约一半的数据，在剩余一半里继续使用折半查找，因此每次都是前一次的约一半的关系。则可以得出折半查找的平均查找长度约为log2n ，记为：

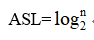
 代码折半查找

/* Note:Your choice is C IDE */
#include "stdio.h"
int  binarysearch(int a[],int c){
    int low,high,mid;
    high=14;
    low=0;
    while(low<=high){
        mid=(low+high)/2;
        if(a[mid]>c){
        high=mid-1;
        }else if(a[mid]<c){
        low=mid+1;
        }else{
        return mid;
        }
    }
    return-1; 
}
void main()
{
    int a[]={1,2,4,5,8,9,12,15,18,25,36,42,52,62,85};
    int c;
    scanf("%d",&c);
    printf("%d\n",binarysearch(a,c));
}

代码-字符定位

#include "stdio.h"
#include "string.h"
int sort(char s[],char sb[],int sta){//sta 为开始查找处
    int i=sta,j=0;
    while(i<(strlen(s))&&j<strlen(sb)){
        if(s[i]==sb[j])
        {
            i++;
            j++;
        }else{
           i=i-j+1;//将开始往后移
           j=0;
        }
    }
    if(j==strlen(sb)){
        return i-strlen(sb);
    }else{
    return -1;}
    }
void main()
{
    int sta=0,len,o;
    char sb[20];
    char s[100]="theanswertoyourkuestionisyes";
    printf("输入字符串:");
    scanf("%s",sb);
    fflush(stdin);
    o=sort(s,sb,sta);
    printf("%d",o);
}