线性回归的推导
什么是线性回归?
回归算法是一种有监督算法
回归算法是一种比较常用的机器学习算法,用于构建一个模型来做特征向量到标签的映射。,用来建立“解释”变量(自变量X)和观测值(因变量Y)之间的关系。在算法的学习过程中,试图寻找一个模型,最大程度拟合训练数据。
回归算法在使用时,接收一个n维度特征向量,输出一个连续的数据值。
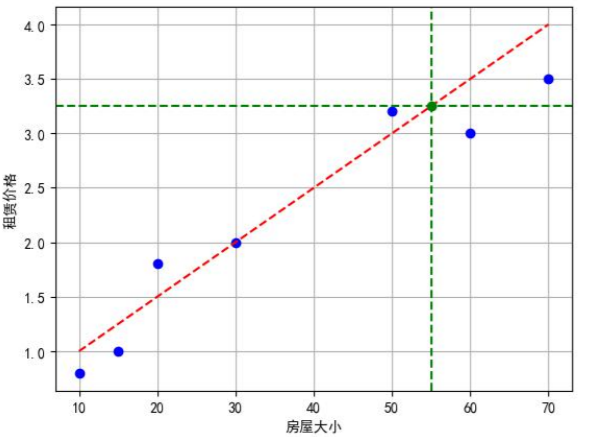
下面通过一则案例引出线性回归:
| 房屋面积(m^2) | 租赁价格(1000¥) |
|---|---|
| 10 | 0.8 |
| 15 | 1 |
| 20 | 1.8 |
| 30 | 2 |
| 50 | 3.2 |
| 60 | 3 |
| 60 | 3.1 |
| 70 | 3.5 |
目的:假如有一个新的房屋面积比如35平方米,那我们应该怎么预测价格?
假设
输入:x特征向量
输出:hθ(x)即预测值
假设拟合函数:
解决方案:
最小二乘法(又称最小平方法)是一种数学优化技术。它由两部分组成:
一、计算所有样本误差的平均(代价函数)
二、使用最优化方法寻找数据的最佳函数匹配(抽象的)
最小二乘法是抽象的,具体的最优化方法有很多,比如正规方程法、梯度下降法、牛顿法、拟牛顿法等等。
线性回归的表达式
选择最优的θ值构成算法公式,并最终要求是计算出θ的值:
预备知识
大数定理
意义
随着样本容量n的增加,样本平均数将接近于总体平均数(期望μ),所以在统计推断中,一般都会使用样本平均数估计总体平均数的值。也就是我们会使用一部分样本的平均值来代替整体样本的期望/均值,出现偏差的可能是存在的,但是当n足够大的时候,偏差的可能性是非常小的,当n无限大的时候,这种可能性的概率基本为0。
作用
就是为使用频率来估计概率提供了理论支持;为使用部分数据来近似的模拟构建全部数据的特征提供了理论支持。
如下图的例子:
从1到10中进行随机抽取数字,经过非常多次循环后,我们发现均值趋向5
import matplotlib.pyplot as plt import random import numpy as np random.seed(28) def generate_random_int(n): return [random.randint(1, 9) for i in range(n)] if __name__ == '__main__': number = 8000 x = [i for i in range(number + 1) if i != 0] total_random_int = generate_random_int(number) y = [np.mean(total_random_int[0:i + 1]) for i in range(number)] plt.plot(x, y, "b-") plt.xlim(0, number) plt.grid(True) plt.show()

中心极限定理
意义
中心极限定理就是一般在同分布的情况下,抽样样本值的规范和在总体数量趋于无穷时的极限分布近似于正态分布。
作用
假设{Xn}为独立同分布的随机变量序列,并具有相同的期望μ和方差为σ2,则{Xn}服从中心极限定理,且Zn为随机序列{Xn}的规范和:
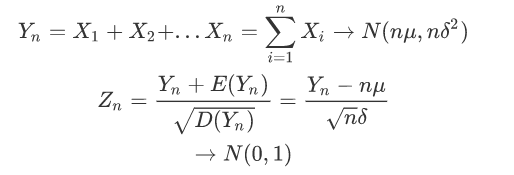
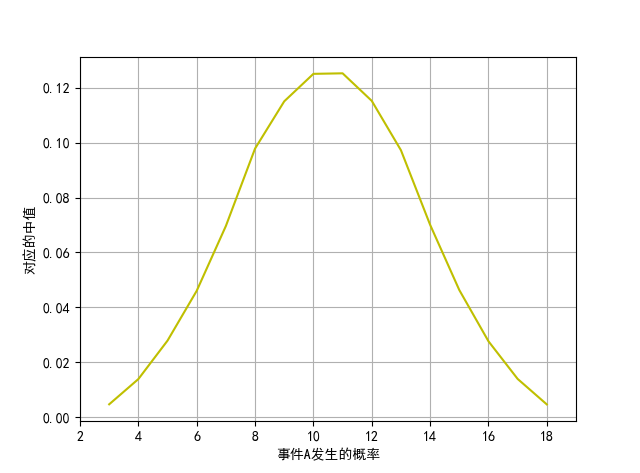
随机的抛六面的骰子,计算三次的点数的和, 三次点数的和其实就是一个事件A,现在问事件A发生的概率以及事件A所属的分布是什么?
import matplotlib.pyplot as plt import random import numpy as np random.seed(28) def generate_random_int(): # 模拟产生筛子 return random.randint(1,6) def generate_mean(n): # 随机选择三个筛子的和 return np.sum([generate_random_int() for i in range(n)]) if __name__ == '__main__': number1 = 1000000 number2 = 3 keys = [generate_mean(number2) for i in range(number1)] result = {} for key in keys: count = 1 if key in result: count+=result[key] result[key] = count x = sorted(np.unique(list(result.keys()))) y = [] for key in x: y.append(result[key]/number1) plt.plot(x,y,"b-") plt.xlim(x[0]-1,x[-1]+1) plt.grid(True) plt.show()
最大似然函数
最大概似估计、极大似然估计,是一种具有理论性的参数估计方法。基本思想是:当从模型总体随机抽取n组样本观测值后,最合理的参数估计量应该使得从模型中抽取该n组样本观测值的概率最大;一般步骤如下:
-
写出似然函数;
-
对似然函数取对数,并整理;
-
求导数;
-
解似然方程
梯度下降
优化思想
用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以梯度下降法也被称为“最速下降法”。梯度下降法中越接近目标值,变量变化越小。计算公式如下:

α被称为步长或者学习率(learningrate),表示自变量θ每次迭代变化的大小。
收敛条件:当目标函数的函数值变化非常小的时候或者达到最大迭代次数的时候,就结束循环。
分类
批量梯度下降法(BatchGradient Descent)
•有N个样本,求梯度的时候就用了N个样本的梯度数据
•优点:准确 缺点:速度慢
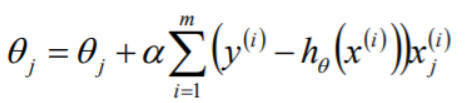
随机梯度下降法(StochasticGradient Descent,SGD)
•和批量梯度下降法原理类似,区别在于求梯度时没有用所有的N个样本的数据,而是仅仅选取一个样本来求梯度
•优点:速度快 缺点:准确度低
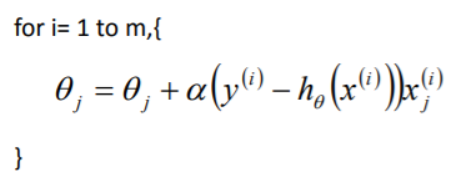
小批量梯度下降法(Mini-batchGradient Descent)
•批量梯度下降法和随机梯度下降法的折衷,比如N=100
•spark中使用的此方法

例子
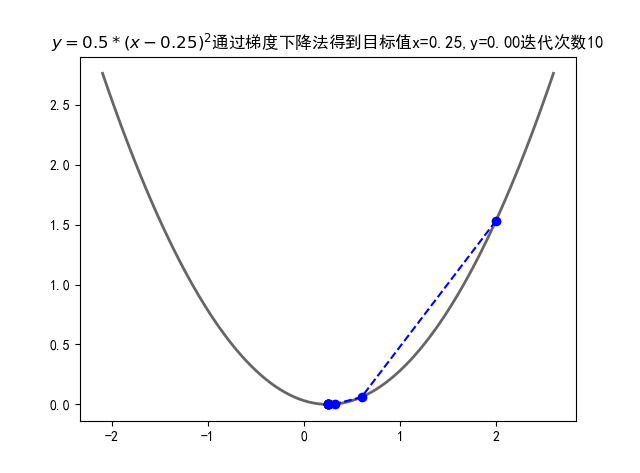
import numpy as np import matplotlib.pyplot as plt def f(x): return 0.5*(x-0.25)**2 def h(x): return x-1/4 X = [] Y = [] x =2 # 此时的学习率,是由一定区间的,过小会导致性能变慢,过大可能发散 step = 0.8 f_change = f(x) f_current = f(x) X.append(x) Y.append(f_current) # 当变化值小于1e-10的时候停止,也就是梯度 while f_change > 1e-10 and len(X)<100: # 这里是梯度下降的变化程度x = x - k*f(x)' x = x - step * h(x) tmp = f(x) f_change = np.abs(f_current - tmp) f_current = tmp X.append(x) Y.append(f_current) fig = plt.figure() X2 = np.arange(-2.1,2.65,0.05) Y2 = 0.5*(X2-0.25)**2 plt.plot(X2,Y2,'-',color="#666666",linewidth = 2) plt.plot(X,Y,'bo--') plt.title("$y= 0.5*(x-0.25)^2$通过梯度下降法得到目标值x=%.2f,y=%.2f迭代次数%d"%(x,f_current,len(X))) plt.show()
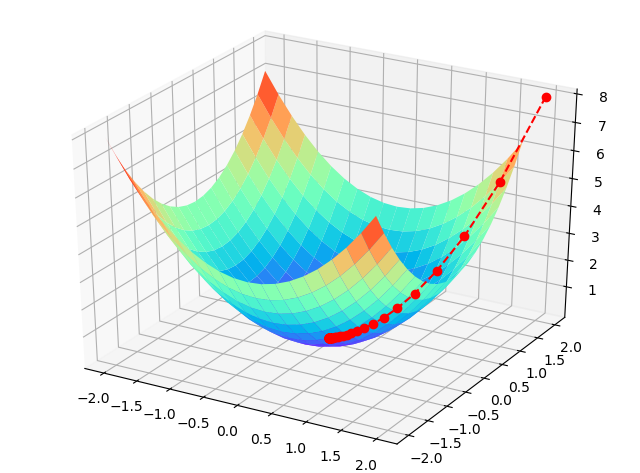
三维数据中的梯度下降
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D def f(x, y): return x ** 2 + y ** 2 def h(t): return 2 * t X = [] Y = [] Z = [] x = 2 y = 2 f_change = x ** 2 + y ** 2 f_current = f(x, y) step = 0.1 X.append(x) Y.append(y) Z.append(f_current) while f_change > 1e-10: # 对于各自未知数求偏导 x = x - step * h(x) y = y - step * h(y) f_change = np.abs(f_current - f(x,y)) f_current = f(x,y) X.append(x) Y.append(y) Z.append(f_current) fig = plt.figure() ax = Axes3D(fig) X2 = np.arange(-2,2,0.2) Y2 = np.arange(-2,2,0.2) X2,Y2 = np.meshgrid(X2,Y2) Z2 = X2**2 + Y2**2 ax.plot_surface(X2,Y2,Z2,rstride=1,cstride=1,cmap='rainbow') ax.plot(X,Y,Z,'ro--') ax.set_title("") plt.show()
推导线性回归
确定目标函数:

首先我们找到的数据,或者在测量的过程中肯定会产生或多或少的数据,所以这里就利用中心极限定理,我们可以将误差epsilon认为是独立分布的服从均值为0方差为σ^2的高斯分布。
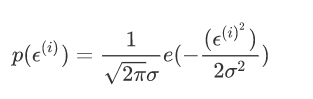
利用最大似然函数来求解:
目标函数为:
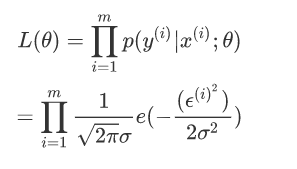
因为累乘求导比较复杂,这里利用对数化,形成对数似然函数:
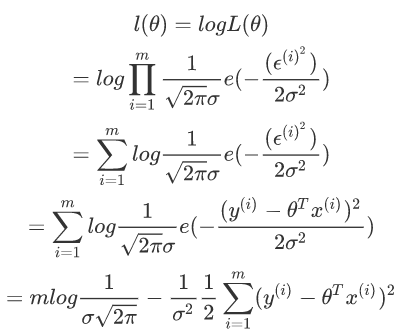
这里我们主要是求似然函数的最大值,前面是常量忽略不计,所以主要是后面的内容。
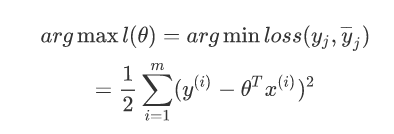
这里的目标函数是平方和损失函数,除了它还有0-1损失函数,感知损失函数,绝对值损失函数,对数损失函数。
利用梯度下降对目标函数θ求解

初始化θ(随机初始化,可以初始为0)沿着负梯度方向迭代,更新后的θ使J(θ)更小
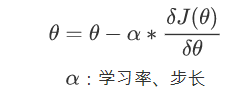
对损失函数进行求导:
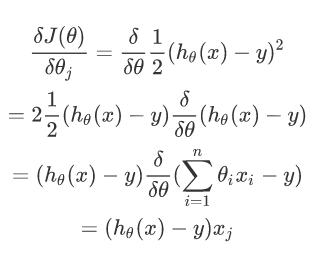
实现代码:
批量下降线性回归:
import numpy as np # 构造训练数据集 x_train = np.array([[2, 0., 3], [3, 1., 3], [0, 2., 3], [4, 3., 2], [1, 4., 4]]) m = len(x_train) print(m) x0 = np.full((m, 1), 1) print(x0) # 构造一个每个数据第一维特征都是1的矩阵 input_data = np.hstack([x0, x_train]) m, n = input_data.shape theta1 = np.array([[2, 3, 4]]).T # 构建标签数据集,后面的np.random.randn是将数据加一点噪声,以便模拟数据集。 # y_train = (input_data.dot(np.array([1, 2, 3, 4]).T)).T y_train = x_train.dot(theta1) + np.array([[2], [2], [2], [2], [2]]) # 设置两个终止条件 loop_max = 1000000 epsilon = 1e-5 # 初始theta np.random.seed(0) # 设置随机种子 theta = np.random.randn(n, 1) # 随机取一个1维列向量初始化theta # 初始化步长/学习率 alpha = 0.00001 # 初始化误差,每个维度的theta都应该有一个误差,所以误差是一个4维。 error = np.zeros((n, 1)) # 列向量 # 初始化偏导数 diff = np.zeros((input_data.shape[1], 1)) # 初始化循环次数 count = 0 while count < loop_max: count += 1 sum_m = np.zeros((n, 1)) for i in range(m): for j in range(input_data.shape[1]): # 计算每个维度的theta diff[j] = (input_data[i].dot(theta) - y_train[i]) * input_data[i, j] # 求每个维度的梯度的累加和 sum_m = sum_m + diff # 利用这个累加和更新梯度 theta = theta - alpha * sum_m # else中将前一个theta赋值给error,theta - error便表示前后两个梯度的变化,当梯度 # 变化很小(在接收的范围内)时,便停止迭代。 if np.linalg.norm(theta - error) < epsilon: break else: error = theta print(theta)
随机梯度线性回归:
# -*- coding: utf-8 -*- """ Created on Wed Nov 28 14:02:17 2018 @author: Administrator """ import numpy as np # 构造训练数据集 x_train = np.array([[2, 0., 3], [3, 1., 3], [0, 2., 3], [4, 3., 2], [1, 4., 4]]) # 构建一个权重作为数据集的真正的权重,theta1主要是用来构建y_train,然后通过模型计算 # 拟合的theta,这样可以比较两者之间的差异,验证模型。 theta1 = np.array([[2 ,3, 4]]).T # 构建标签数据集,y=t1*x1+t2*x2+t3*x3+b即y=向量x_train乘向量theta+b, 这里b=2 y_train = (x_train.dot(theta1) + np.array([[2],[2],[2],[2],[2]])).ravel() # 构建一个5行1列的单位矩阵x0,然它和x_train组合,形成[x0, x1, x2, x3],x0=1的数据形式, # 这样可以将y=t1*x1+t2*x2+t3*x3+b写为y=b*x0+t1*x1+t2*x2+t3*x3即y=向量x_train乘向 # 量theta其中theta应该为[b, *, * , *],则要拟合的theta应该是[2,2,3,4],这个值可以 # 和算出来的theta相比较,看模型的是否达到预期 x0 = np.ones((5, 1)) input_data = np.hstack([x0, x_train]) m, n = input_data.shape # 设置两个终止条件 loop_max = 10000000 epsilon = 1e-6 # 初始化theta(权重) np.random.seed(0) theta = np.random.rand(n).T # 随机生成10以内的,n维1列的矩阵 # 初始化步长/学习率 alpha = 0.000001 # 初始化迭代误差(用于计算梯度两次迭代的差) error = np.zeros(n) # 初始化偏导数矩阵 diff = np.zeros(n) # 初始化循环次数 count = 0 while count < loop_max: count += 1 # 没运行一次count加1,以此来总共记录运行的次数 # 计算梯度 for i in range(m): # 计算每个维度theta的梯度,并运用一个梯度去更新它 diff = input_data[i].dot(theta)-y_train[i] theta = theta - alpha * diff*(input_data[i]) # else中将前一个theta赋值给error,theta - error便表示前后两个梯度的变化,当梯度 #变化很小(在接收的范围内)时,便停止迭代。 if np.linalg.norm(theta - error) < epsilon: # 判断theta与零向量的距离是否在误差内 break else: error = theta print(theta)
小批量梯度下降
import numpy as np # 构造训练数据集 x_train = np.array([[2, 0., 3], [3, 1., 3], [0, 2., 3], [4, 3., 2], [1, 4., 4]]) m = len(x_train) x0 = np.full((m, 1), 1) # 构造一个每个数据第一维特征都是1的矩阵 input_data = np.hstack([x0, x_train]) m, n = input_data.shape theta1 = np.array([[2, 3, 4]]).T # 构建标签数据集,后面的np.random.randn是将数据加一点噪声,以便模拟数据集。 # y_train = (input_data.dot(np.array([1, 2, 3, 4]).T)).T y_train = x_train.dot(theta1) + np.array([[2], [2], [2], [2], [2]]) # 设置两个终止条件 loop_max = 1000000 epsilon = 1e-5 # 初始theta np.random.seed(0) # 设置随机种子 theta = np.random.randn(n, 1) # 随机取一个1维列向量初始化theta # 初始化步长/学习率 alpha = 0.00001 # 初始化误差,每个维度的theta都应该有一个误差,所以误差是一个4维。 error = np.zeros((n, 1)) # 列向量 # 初始化偏导数 diff = np.zeros((input_data.shape[1], 1)) # 初始化循环次数 count = 0 # 设置小批量的样本数 minibatch_size = 2 while count < loop_max: count += 1 sum_m = np.zeros((n, 1)) for i in range(1, m, minibatch_size): # for j in range(i - 1, i + minibatch_size - 1, 1): # # 计算每个维度的theta # diff[j] = (input_data[i].dot(theta) - y_train[i]) * input_data[i, j] diff = (1/minibatch_size)*input_data[i:i+minibatch_size,:].T.dot(input_data[i:i+minibatch_size,:].dot(theta) - y_train[i:i+minibatch_size,:]) # 求每个维度的梯度的累加和 sum_m = sum_m + diff # 利用这个累加和更新梯度 theta = theta - alpha * (1.0 / minibatch_size) * sum_m # else中将前一个theta赋值给error,theta - error便表示前后两个梯度的变化,当梯度 # 变化很小(在接收的范围内)时,便停止迭代。 if np.linalg.norm(theta - error) < epsilon: break else: error = theta # 和sklearn库相对比 # from sklearn.linear_model import LinearRegression # model = LinearRegression(fit_intercept=False) # model.fit(input_data,y_train) # print(model.coef_) print(theta)
线性回归和正则化
向量范数
1-范数:即向量元素绝对值之和,调用函数np.linalg.norm(x, 1)
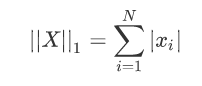
2-范数:Euclid范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方 和再开方,调用函数np.linalg.norm(x) (默认为2)
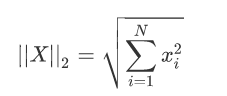
无穷大范数:即所有向量元素绝对值中的最大值,调用函数np.linalg.norm (x, np.inf)
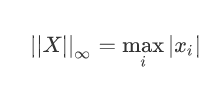
无穷小范数:即所有向量元素绝对值中的最小值,调用函数np.linalg.norm (x, -np.inf)

p-范数即向量元素绝对值的p次方和的1/p次幂,调用函数np.linalg.norm (x, p)
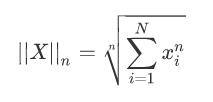
下图表示了p从无穷到0变化时,三维空间中到原点的距离(范数)为1的点构成的图形的变化情况。

经验风险和结构风险(可跳过)
期望风险表示的是全局的概念,表示的是决策函数对所有的样本(X,Y)预测能力的大小,而经验风险则是局部的概念,仅仅表示决策函数对训练数据集里样本的预测能力。理想的模型(决策)函数应该是让所有的样本的损失函数最小的(也即期望风险最小化),但是期望风险函数往往是不可得到的,即上式中,X与Y的联合分布函数不容易得到。现在我们已经清楚了期望风险是全局的,理想情况下应该是让期望风险最小化,但是呢,期望风险函数又不是那么容易得到的。怎么办呢?那就用局部最优的代替全局最优这个思想吧。这就是经验风险最小化的理论基础。
通过上面的分析可以知道,经验风险与期望风险之间的联系与区别。现在再总结一下:
经验风险是局部的,基于训练集所有样本点损失函数最小化的。
期望风险是全局的,是基于所有样本点的损失函数最小化的。
经验风险函数是现实的,可求的;
期望风险函数是理想化的,不可求的;
只考虑经验风险的话,会出现过拟合的现象,过拟合的极端情况便是模型f(x)对训练集中所有的样本点都有最好的预测能力,但是对于非训练集中的样本数据,模型的预测能力非常不好。怎么办呢?这个时候就引出了结构风险。结构风险是对经验风险和期望风险的折中。在经验风险函数后面加一个正则化项(惩罚项)便是结构风险了。如下式:

相比于经验风险,结构风险多了一个惩罚项,其中是一个l是一个大于0的系数。J(f)表示的是模型f的复杂度。结构风险可以这么理解:
经验风险越小,模型决策函数越复杂,其包含的参数越多,当经验风险函数小到一定程度就出现了过拟合现象。也可以理解为模型决策函数的复杂程度是过拟合的必要条件,那么我们要想防止过拟合现象的发生,就要破坏这个必要条件,即降低决策函数的复杂度。也即,让惩罚项J(f)最小化,现在出现两个需要最小化的函数了。我们需要同时保证经验风险函数和模型决策函数的复杂度都达到最小化,一个简单的办法把两个式子融合成一个式子得到结构风险函数然后对这个结构风险函数进行最小化。

简而言之,经验风险最小化可以理解为:最小化代价函数结构风险最小化可以理解为:最小化目标函数(代价函数+正则化项)
为什么要引入正则项
为了防止数据过拟合,也就是的θ值在样本空间中不能过大/过小,可以在目标函数之上增加一个平方和损失: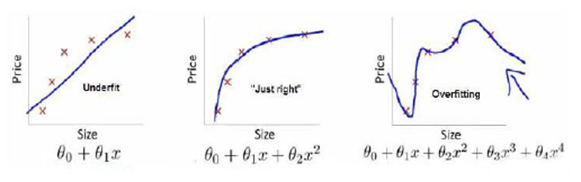
Ridge回归
L2正则化:权值向量w中各个元素的平方和
上面我们一直使用θ的平方作为正则项也就是L2正则,它的学名叫做Ridge回归或者岭回归,
Lasso回归
L1正则化:权值向量w中各个元素的绝对值之和
L1正则化 VS L2正则化
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择。
L2正则化可以防止模型过拟合(overfitting)
为什么 L1 正则可以产生稀疏模型(很多参数=0),而L2 正则不会出现很多参数为0的情况?

由图可知左面式L1正则,右面是L2正则,这里左面更容易和超平面在y轴上形成最优解,此时x=0也就是产生了稀疏解,这正是我们大多说时候想要的。
Elasitc Net
同时使用L1正则和L2正则的线性回归模型就称为Elasitc Net算法(弹性网络算法)
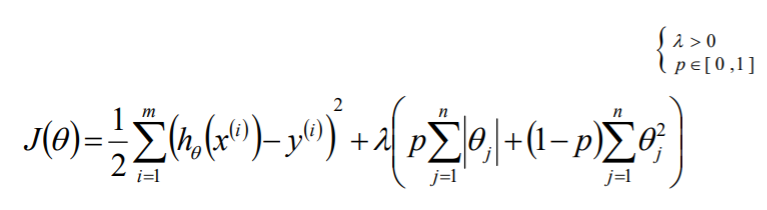
到此线性回归以及优化已经全部总结,训练结束后可以使用MSE,RMSE,R^2这些指标进行评估。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号