20162307 2017-2018-1 《程序设计与数据结构》第11周学习总结
20162307 2017-2018-1 《程序设计与数据结构》第11周学习总结
教材学习内容总结(第十九章 图)
19.0 概述
- 本章是在讲图及它的特殊用途
- 讨论有向图和无向图
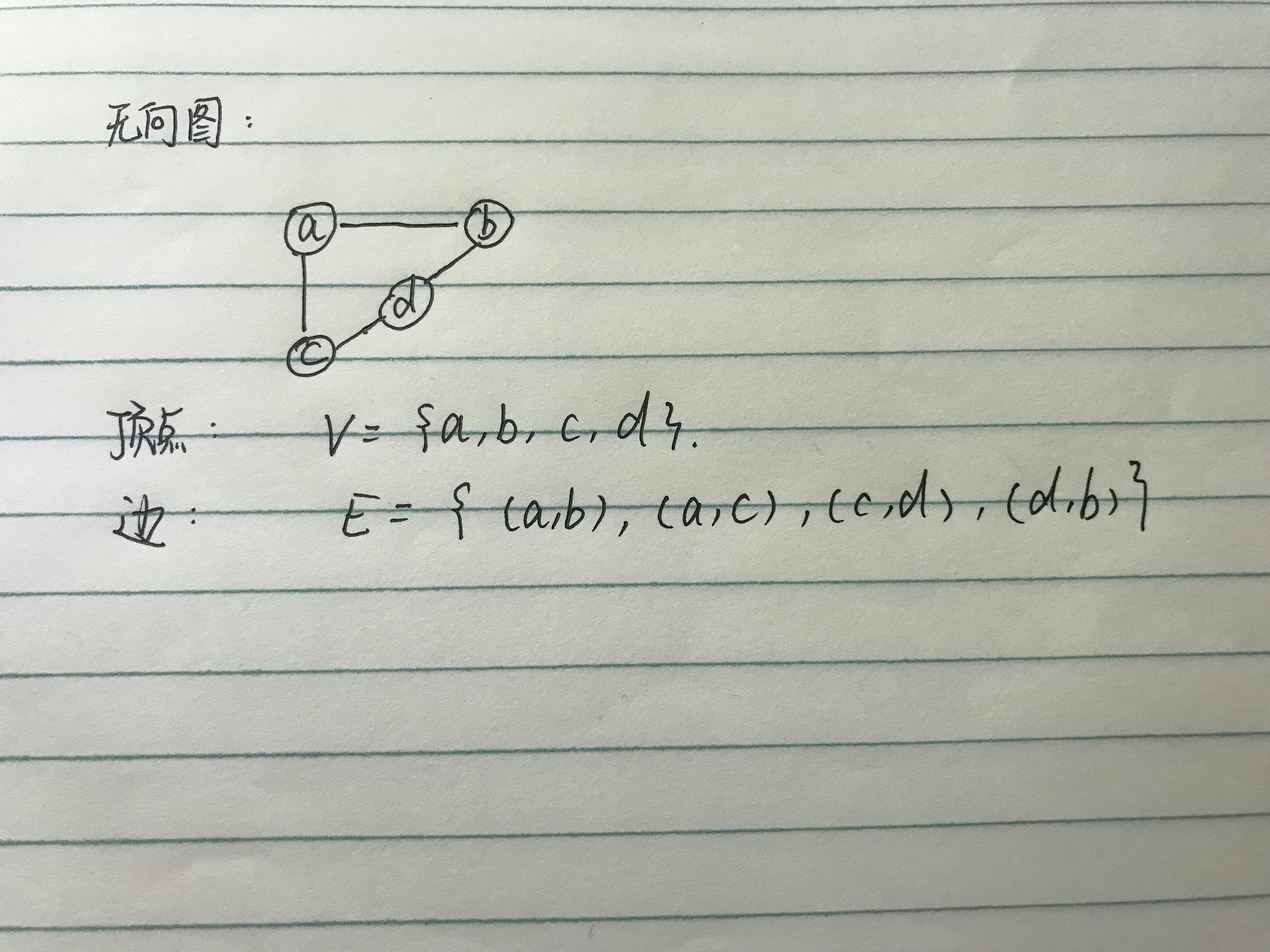
19.1 无向图
- 无向图中,表示边的顶点对是无序的
- 含有最多条边的无向图称为完全图
- 实际上,树就是图
- 如果图中的两个顶点之间有边连接,则称它们是邻接的
- 路径是图中连接两个顶点的边的序列
- 如果无向图中任意两个顶点间都有路径,则无向图称为连通的
- 第一个顶点和最后一个顶点相同且边不重复的路径称为环
- 一颗无向树是连通的、无环的无向图,其中的一个元素表示根
19.2 有向图
-
在有向图中,边是顶点的有序对
-
有向图中的路径是连接图中两个顶点的有向边的序列
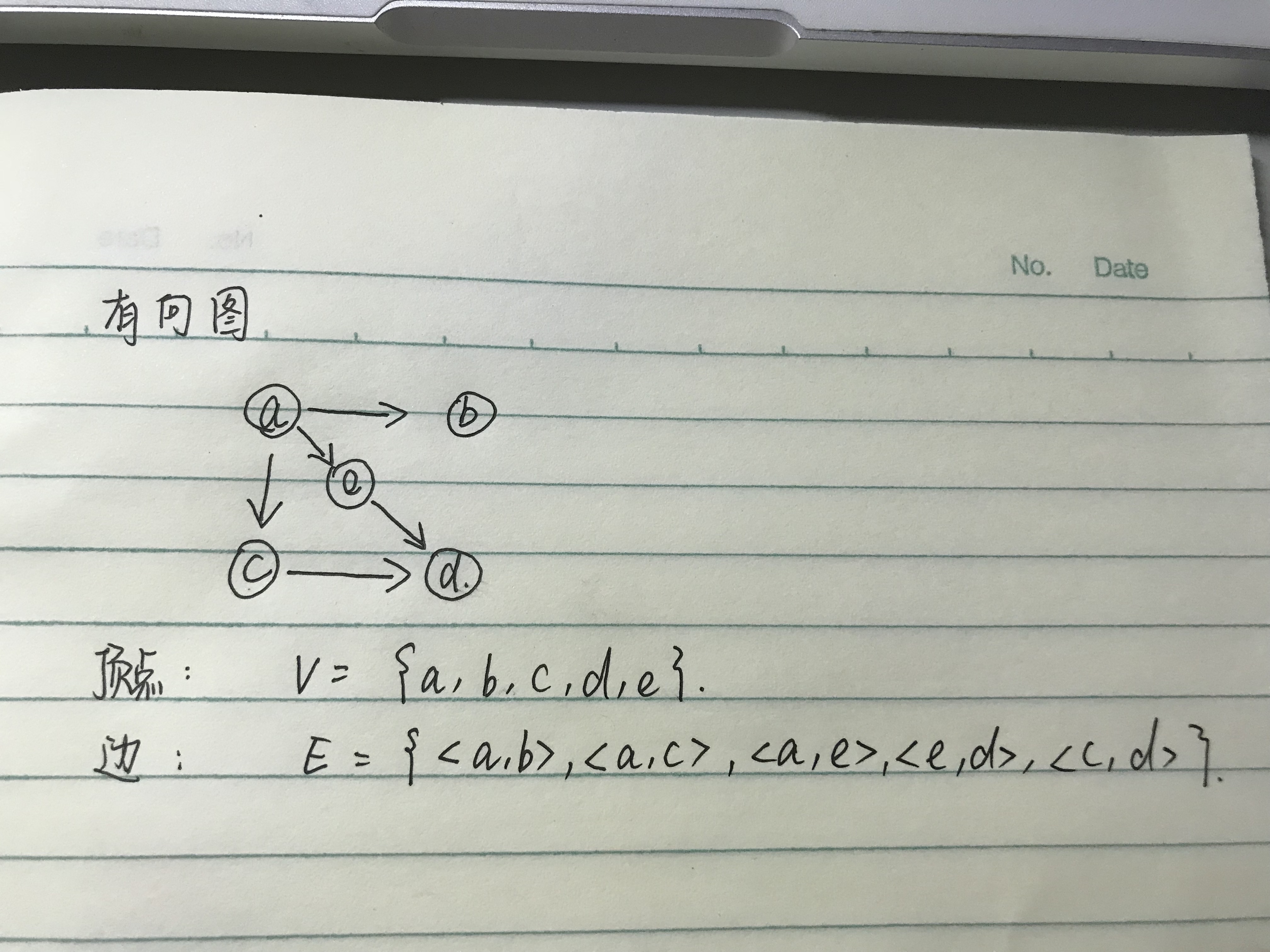
-
如果有向图中任意两个顶点之间都有路径相连,则图为有向连通图
-
有向树是一个有向图,其中指定一个元素为根,并具有下列特性:
- 任何顶点到根都没有连接
- 到达每个非根元素的连接都只有一个
- 从根到每个顶点都有路径
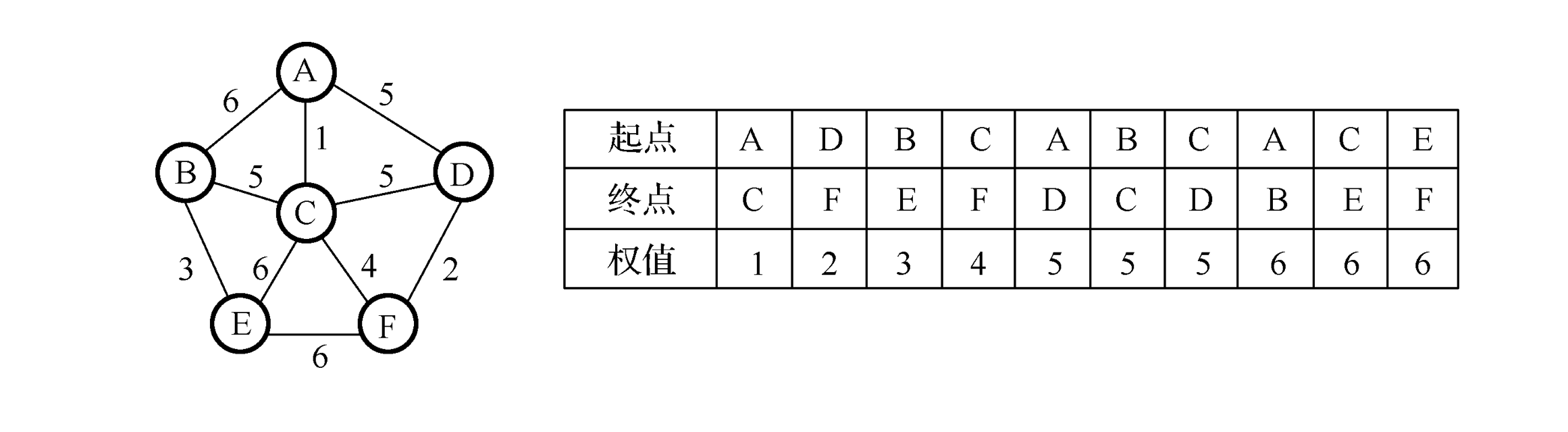
19.3 带权图
- 图的每条边上都有对应的权值的图称为带权图
- 根据需要,带权图既可以是无向的也可以是有向的
- 对于带权图来说,使用由起始点、结束点及权构成的三元组成表示每条边。
- 对于有向图,每条有向边必须使用一个三元组表示
19.4 常用的图算法
- 图的几个常用算法可用于无向图、有向图及/或带权图
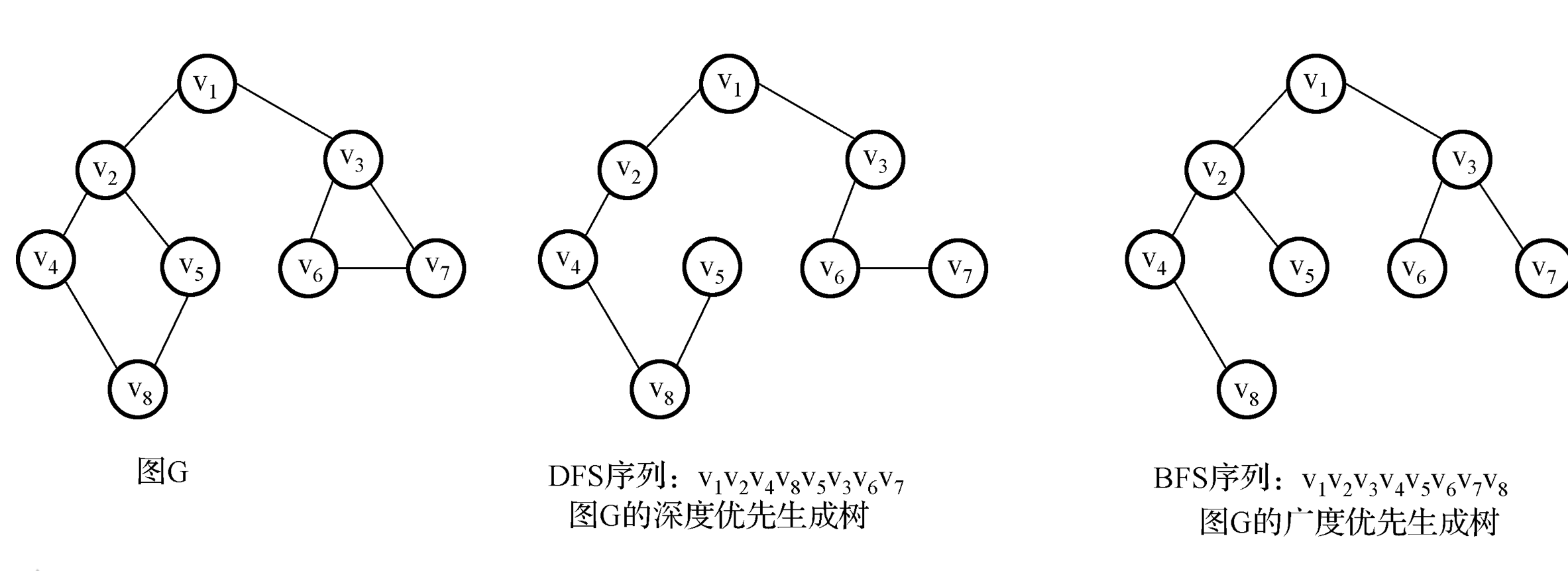
19.4.1 遍历
- 图的遍历一般有两种:类似树的层序遍历的广度优先遍历;类似树的先序遍历的深度优先遍历
顶部伪代码(广度优先遍历)
(1)顶点v入队列。
(2)当队列非空时则继续执行,否则算法结束。
(3)出队列取得队头顶点v;访问顶点v并标记顶点v已被访问。
(4)查找顶点v的第一个邻接顶点w。
(5)若v的邻接顶点w未被访问过的,则w入队列。
(6)继续查找顶点v的另一个新的邻接顶点w,转到步骤(5)。
直到顶点v的所有未被访问过的邻接点处理完。转到步骤(2)。
伪代码的细化描述(广度优先遍历)
设立一个访问标志数组visited[N],初值为0,某顶点被访问后,则相应下标元素置1。
(1)初始化队列Q;visited[N]=0;
(2)访问顶点v;visited[v]=1;顶点v入队列Q;
(3) while(队列Q非空)
v = 队列Q的队头元素出队;
w = 顶点v的第一个邻接点;
while ( w存在 )
如果w未访问,则访问顶点w;
visited[w]=1;
顶点w入队列Q;
w=顶点v的下一个邻接点。
public Iterator<T> iteratorBFS(int startIndex){ //广度优先遍历
int currentVertex;
LinkedQueue<Integer> traversalQueue = new LinkedQueue <Integer> ();
ArrayIterator<T> iter =new ArrayIterator <T> ();
if (!indexIsValid(startIndex)){
return iter;
}
boolean[] visited =new boolean[numVertices];
for (int vertexIndex=0;vertexIndex<numVertices;vertexIndex++)
visited[vertexIndex]=false;traversalQueue.enqueue ( startIndex );
visited[startIndex]=true;
while (!traversalQueue.isEmpty ()){
currentVertex=traversalQueue.dequeue ();
iter.add (vertices[currentVertex]);
for(int vertexIndex=0;vertexIndex<numVertices;vertexIndex++)
if (adjMatrix[currentVertex][vertexIndex]&&!visited[vertexIndex]){
traversalQueue.enqueue ( vertexIndex );
visited[vertexIndex]=true;
}
}
return iter;
}
- 利用队列管理遍历过程,用迭代器得到结果
19.4.2 测试连通性
- 如果图中任意两个顶点间都有路径相连,则为连通图。这个定义对无向图和有向图都成立
- 当且仅当从任意顶点开始的广度优先遍历中得到的顶点数等于图中所含有的顶点数时,图是连通的。
--
19.4.3 最小生成树
- 生成树是包含图中所有顶点及图中部分(可能不是全部)边的一棵树
- 最小生成树是其所含边的权值之和小于等于图的任意其他生成树的边的权值之和的生成树
最小生成树构造思路
设T为最小生成树集合
最小生成树集合包括n个顶点与n-1条边
(1) 初始T= 空集合
(2) while ( T 还不是生成树)
(3) 找出对 T 来说不会形成回路且权值最小的边 (u,v)
(4) 将边(u, v)加入T中
(5) return T
19.4.4 Prim(普里姆)算法
- 从连通网络 N = { V, E }中的某一顶点 u0 出发, 选择与它关联的具有最小权值的边(u0, v),将其顶点加入到生成树顶点集合U中。
以后每一步从一个顶点在 U 中, 而另一个顶点不在 U 中的各条边中选择权值最小的边(u, v),把它的顶点加入到集合 U 中。如此继续下去, 直到网络中的所有顶点都加入到生成树顶点集合 U 中为止。
伪代码细化描述:
建立候选边集表,把从起始点u0 出发到其余各点的权值记录在其中,开始u= u0
(1)在候选边集中选择结点u;
(2)在候选边集中选出最短边(u, v);
(3)以v为起点,调整候选边集;
调整方法:当(u, x)>(v, x)时,用(v, x)替换(u, x),x为除u、v外的其他点;
重复(1)~(3)直到所有结点都处理完毕。

19.4.5 Kruskal算法
- 从边出发,直接找最小权值的边来构建生成树

CRC
什么是CRC
- 循环冗余校验(Cyclic Redundancy Check, CRC)是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数,主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的原理来作错误侦测的。
生成CRC码的基本原理
- 任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。

CRC校验码软件生成方法
借助于多项式除法,其余数为校验字段。
例如:信息字段代码为: 1011001;对应m(x)=x6+x4+x3+1
假设生成多项式为:g(x)=x4+x3+1;则对应g(x)的代码为: 11001
x4m(x)=x10+x8+x7+x4 对应的代码记为:10110010000;
采用多项式除法: 得余数为: 1010 (即校验字段为:1010)
发送方:发出的传输字段为: 1 0 1 1 0 0 1 1 0 10
接收方:使用相同的生成码进行校验,接收到的字段/生成码(二进制除法)如果能够除尽,则正确
教材学习中的问题和解决过程
代码调试中的问题和解决过程
代码托管
上周考试错题总结
结对及互评
本周结对学习情况
- [20162303](http://www.cnblogs.com/syx390234975/)
- 结对学习内容
- 学习第十九章
- 研究上课时讲的ppt
其他(感悟、思考等,可选)
成功不是属于先出发的,而是最先到达跟最后倒下的;
成功不是属于先做的,而是属于做的最好的那一个人。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 68/68 | 1/1 | 12/12 | |
| 第三周 | 298/366 | 2/3 | 18/30 | |
| 第五周 | 688/1162 | 2/5 | 20/50 | |
| 第七周 | 1419/2581 | 4/9 | 20/70 | |
| 第八周 | 908/3489 | 2/11 | 20/90 | |
| 第九周 | 663/4152 | 2/13 | 20/110 | |
| 第十周 | 998/5154 | 3/16 | 20/130 | |
| 第十一周 | 118/5272 | 3/19 | 20/150 |
尝试一下记录「计划学习时间」和「实际学习时间」,到期末看看能不能改进自己的计划能力。这个工作学习中很重要,也很有用。
耗时估计的公式
:Y=X+X/N ,Y=X-X/N,训练次数多了,X、Y就接近了。
-
计划学习时间:20小时
-
实际学习时间:20小时
(有空多看看现代软件工程 课件
软件工程师能力自我评价表)





