20162307 2017-2018-1 《程序设计与数据结构》第9周学习总结

20162307 2017-2018-1 《程序设计与数据结构》第9周学习总结

教材学习内容总结(第十八章 堆和优先队列)

18.0 概述

  • 本章是在讲堆及它的特殊用途
  • 讨论堆的链式实现方式
  • 讨论堆排序
  • 优先队列和优先队列与堆的关系

18.1 堆

  • 堆：是一颗完全二叉树，其中每个元素都要大于或小于他的所有的孩子
  • 分类：最大堆、最小堆
  • 堆与完全二叉树的区别：在二叉排序树中，某结点的右孩子结点的值一定大于该结点的左孩子结点的值；在堆中却不一定，堆只是限定了某结点的值大于（或小于）其左右孩子结点的值，但没有限定左右孩子结点之间的大小关系。

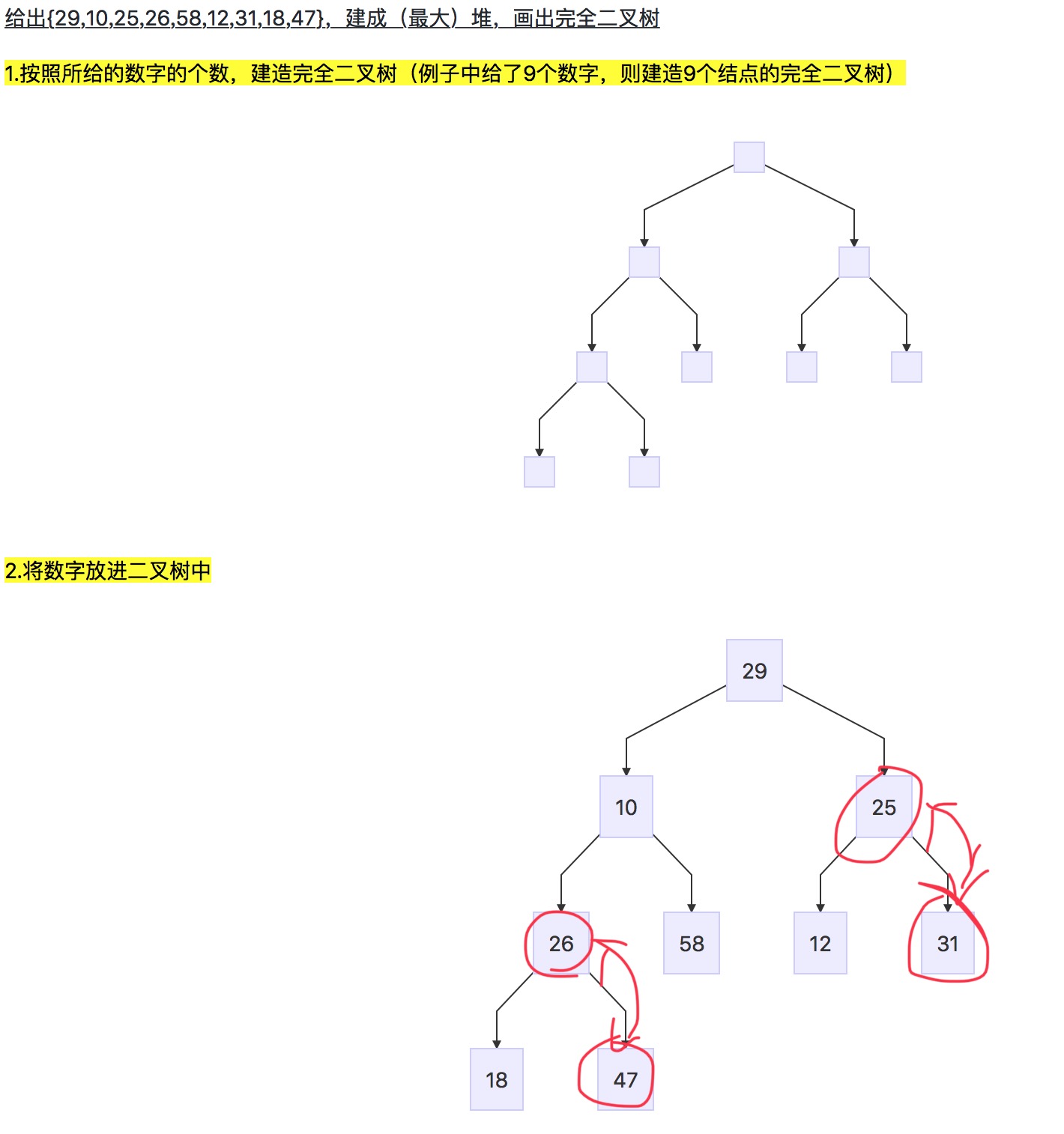
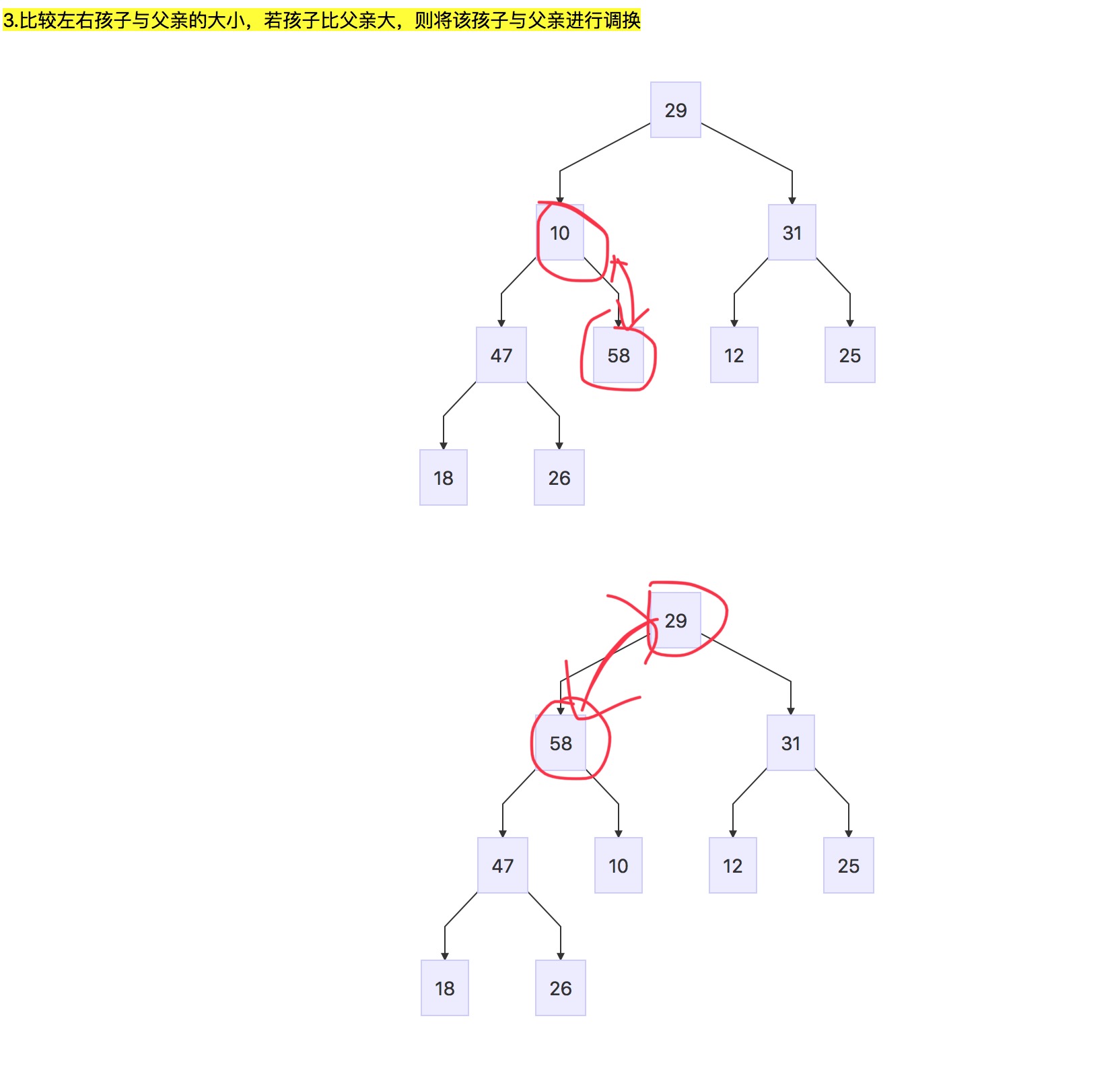
18.1.1 向堆中添加一个元素

  • 添加新元素的策略：将元素添加为新的叶结点，同时保持树是完全树，然后将该元素向根的方向移动，将它与父节点对换，直到其中的元素大小关系满足要求为止

  • 添加新元素的代码

      public void add (T element)
      {
          HeapNode<T> node = new HeapNode<T>(element);
          HeapNode<T> newParent = null;

          if (root == null)
              root = node;
          else
          {
              newParent = ((HeapNode<T>)root).getParentAdd(last);

              if (newParent.left == null)
                  newParent.setLeft(node);
              else
                  newParent.setRight(node);
          }

          node.setParent(newParent);
          last = node;

          ((HeapNode<T>)root).heapifyAdd(last);
      }

18.1.2 从堆中删除最大元素

  • 由堆（最大堆）的特性可知，最大元素就是根，所以应该是删除根结点，然后将余下的两个分开的子树重新构造成堆

  • 重构堆的策略：删除最后一层最右边的叶结点，将它放在根上，然后将它在树中下移至满足元素关系的位置。

  • 参考博客

18.2 堆的实现

  • 以最大堆为例，MaxHeap接口，对于堆来说，这个接口包含了add（添加一个新元素）、getMax（获取最大值）、removeMax（删除最大值）

      public void add (T element)
      {
          HeapNode<T> node = new HeapNode<T>(element);
          HeapNode<T> newParent = null;
          if (root == null)
              root = node;
          else
          {
              newParent = ((HeapNode<T>)root).getParentAdd(last);

              if (newParent.left == null)
                  newParent.setLeft(node);
              else
                  newParent.setRight(node);
          }
          node.setParent(newParent);
          last = node;
          ((HeapNode<T>)root).heapifyAdd(last);
      }   
      public T removeMax()
      {
          if (root == null)
              throw new EmptyCollectionException ("Remove max operation " +
              "failed. Tree is empty.");
          T maxElement = root.getElement();
          if (root.count() == 1)
              root = last = null;
          else
          {
              HeapNode<T> newLast = ((HeapNode<T>)root).getNewLastNode(last);
              if (last.parent.left == last)
                  last.parent.left = null;
              else
                  last.parent.right = null;
              root.setElement(last.getElement());
              last = newLast;
              ((HeapNode<T>)root).heapifyRemove((HeapNode<T>)root);
          }
          return maxElement;
      }
       public T getMax() {
          if (root==null){
          throw new EmptyCollectionException ( "Get max element" +
                      "failed.Tree is empty.");}
              return root.getElement ();        
          }

18.3 堆排序

  • 堆排序就是先将一组元素一项一项地插入到堆中，然后一次删除一个

18.4 优先队列

  • 优先队列是一个服从两个有序规则的集合。
  • 两个有序规则是：A 具有更高优先级的项排在前面 B 具有相同优先级的项按先进先出的规则排列

CRC

什么是CRC

  • 循环冗余校验(Cyclic Redundancy Check, CRC)是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数，主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的原理来作错误侦测的。

生成CRC码的基本原理

  • 任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。

CRC校验码软件生成方法

    借助于多项式除法，其余数为校验字段。
    例如：信息字段代码为: 1011001；对应m(x)=x6+x4+x3+1 
          假设生成多项式为：g(x)=x4+x3+1；则对应g(x)的代码为: 11001
          x4m(x)=x10+x8+x7+x4 对应的代码记为：10110010000；
    采用多项式除法:  得余数为: 1010     (即校验字段为：1010）
    发送方：发出的传输字段为:  1 0 1 1 0 0 1 1 0 10
    接收方：使用相同的生成码进行校验,接收到的字段/生成码（二进制除法）如果能够除尽，则正确

教材学习中的问题和解决过程

问题一

  • 问题：
    在书上18.4优先队列中看到

优先队列是一个服从两个有序规则的集合。
两个有序规则是：A 具有更高优先级的项排在前面 B 具有相同优先级的项按先进先出的规则排列

不是很清楚优先队列是什么，既然是优先队列，还在堆这章出现，那么优先队列、堆、队列有什么联系和区别呢？

队列的特点是先进先出。通常都把队列比喻成排队买东西，大家都很守秩序，先排队的人就先买东西。
但是优先队列有所不同，它不遵循先进先出的规则，而是根据队列中元素的优先权，优先权最大的先被取出。通常把优先队列比喻成现实生活中的打印。一个打印店里有很多打印机，每台机器的性能不一样，有的打印机打印很快，有的打印机打印速度很慢。当这些打印机陆陆续续打印完自己的任务时进入排队等候状态。如果我这个时候要打印一份文件，我选的不是第一个排队的打印机，而是性能最好，打印最快的打印机。

代码调试中的问题和解决过程

问题一

书上18.4和18.5打出来，发现出现错误
addElement处和removeMin处

在PriorityQueueNode中没有addElement方法，有add，所以将addElement改为add
removeMin是移除最小值，然而PriorityQueueNode中只有移除最大值，所以将removeMin改为removeMax

代码托管

上周考试错题总结

  • describes叙述; 形容; 描写( describe的第三人称单数 ); 画出
  • balanced tree平衡树
  • balanced平稳的，平衡的; 和谐的，有条不紊的; 安定的; “balance”的过去式和过去分词
  • nodes节( node的名词复数 ); 节点; 结节; 植物的节
  • exactly the same一丝不差；毫发不差
  • at one一致，合力
  • all of实足，不少于
  • each other互相，彼此
  • none of都不
  • defines规定( define的第三人称单数 ); 使明确; 精确地解释; 画出…的线条

结对及互评

本周结对学习情况

- [20162303](http://www.cnblogs.com/syx390234975/)
- 结对学习内容
    - 学习第十八章
    - 研究上课时讲的ppt

其他（感悟、思考等，可选）

成功不是属于先出发的，而是最先到达跟最后倒下的；
成功不是属于先做的，而是属于做的最好的那一个人。

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 68/68 1/1 12/12
第三周 298/366 2/3 18/30
第五周 688/1162 2/5 20/50
第七周 1419/2581 4/9 20/70
第八周 908/3489 2/11 20/90
第九周 663/4152 2/13 20/110

尝试一下记录「计划学习时间」和「实际学习时间」，到期末看看能不能改进自己的计划能力。这个工作学习中很重要，也很有用。
耗时估计的公式
：Y=X+X/N ，Y=X-X/N，训练次数多了，X、Y就接近了。

参考：软件工程软件的估计为什么这么难，软件工程 估计方法

  • 计划学习时间:20小时

  • 实际学习时间:20小时

(有空多看看现代软件工程 课件
软件工程师能力自我评价表)

参考资料

posted @ 2017-11-04 17:49  张韵琪  阅读(320)  评论(0)  编辑  收藏  举报