P2822组合数问题

组合数问题（NOIP2016提高组Day2T1）

Time Limit:1000MS  Memory Limit:512000K

【题目描述】

组合数表示的是从n个物品中选出m个物品的方案数。举个例子，从（1,2,3) 三个物品中选择两个物品可以有（1,2),(1,3),(2,3)这三种选择方法。根据组合数的定 义，我们可以给出计算组合数的一般公式：

 

小葱想知道如果给定n,m和k，对于所有的0<=i<= n，0<=j<= min(i,m)有多少对 (i,j)满足是k的倍数。

【输入格式】

第一行有两个整数t,k，其中t代表该测试点总共有多少组测试数据，k的意义见【问题描述】。
接下来t行每行两个整数n,m，其中n,m的意义见【问题描述】。

【输出格式】

t行，每行一个整数代表答案。

【输入样例1】

1 2
3 3

【输出样例1】

1

【输入样例2】

2 5
4 5
6 7

【输出样例2】

0
7

【数据范围】

来一波数学讲解

 

 

 

 首先 来一个非常神奇的杨辉三角

 

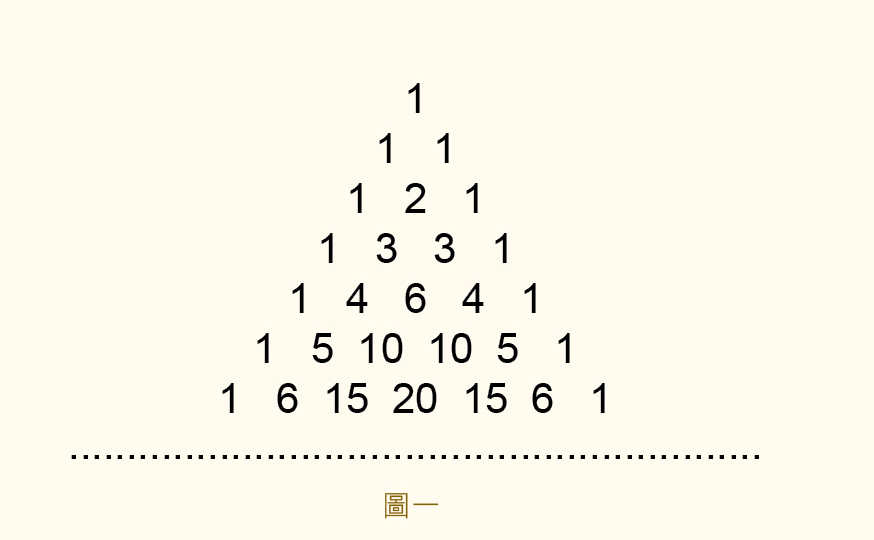
那么首先我们知道

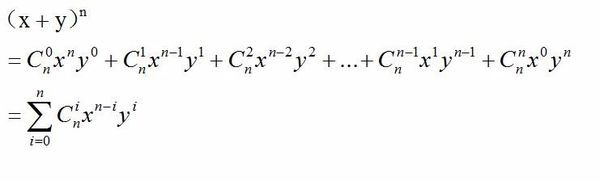
也就是说杨辉三角上的数都是组合数

第i行第j列就是C(i,j)

C(n,m)=C(n-1,m)+C(n-1,m-1)

这个公式竟然就是杨辉三角的递推式！

也就是说我们就是在杨辉三角上寻找Cij是k的倍数！！！

那么我们可以先一波预处理求出来杨辉三角

and then? 突然之间，好像自己又蒙了。。。

不急！

 

 

我们不妨再重新分析一下

Cij 就是在杨辉三角上第i行第j列的那个数

我们只需要把杨辉三角全扫一遍!?

但是题目要查询多组数据

最大要查询10^4次，这就很尴尬了，不太好整！如果我们每一次都扫一遍，那这简直就是天方夜谭！

我们这里用了一个非常神奇的东西：二维前缀和优化

我们可以把一个矩形表示出来i行j列（其实更像一个平行四边形） 用一个二维的前缀和数组来求往上的区间里的所有的可行解

这样先预处理出来，每次查询直接输出答案就行啦

 

还有一个要注意的要多模几次k!

 

#include<bits/stdc++.h>
using namespace std;
int C[2005][2005];//杨辉三角组合数数组 
int ans[2005][2005];
int main()
{
    int t,k;
    cin>>t>>k;
    C[1][1]=1;
    for(int i=0;i<=2000;i++) 
        C[i][0]=1;
    for(int i=2;i<=2000;i++){
        for(int j=1;j<=i;j++)
            C[i][j]=(C[i-1][j-1]+C[i-1][j])%k;
    }
    for(int i=2;i<=2000;i++){
        for(int j=1;j<=i;j++){
            ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];
            if(C[i][j]==0)//是k的倍数
                ans[i][j]++; 
        }
        ans[i][i+1]=ans[i][i];
    }
/*    for(int i=1;i<=20;i++){
        for(int j=1;j<=i;j++)
            cout<<ans[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
    for(int i=1;i<=20;i++){
        for(int j=1;j<=i;j++)
            cout<<C[i][j]<<" ";
        cout<<endl;
    }*/
    while(t--){
        int n,m;
        cin>>n>>m;
        if(n<m)
            m=n;
        cout<<ans[n][m]<<endl;
    }
    return 0;
}