如何实现二叉树和二叉树的遍历（java）

什么是二叉树？

 二叉树是一种树状结构，其特点是每个结点至多只有两颗子树（即二叉树中不存在度大于2的结点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。

与树相似，二叉树也以递归的形式定义。二叉树是n(n≥0)个结点的有限集合：
①或者为空二叉树，及n=0。
②或者由一个根结点和两个互不相交的称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
二叉树有五种不同的基本形态： A：空二又树 B：只有一个根结点的二叉树 C：右子树为空的二叉树 D：左子树为空的二叉树 E：左、右子树都非空的二叉树

 

如何实现二叉树

 

1.链表的形式

创建二叉树的节点类，二叉树由数据域，两个指向孩子节点的引用组成，多个节点类连接起来就形成了二叉树。

实现代码：

public class TreeNode {

    public int value;//数据域
    public TreeNode left;//指向左子树
    public TreeNode right;//指向右子树

    public TreeNode(int value, TreeNode left, TreeNode right) {
        this.value = value;
        this.left = left;
        this.right = right;
    }

    public TreeNode(int value){
        this.value=value;
        left=null;
        right=null;
    }
}

 

2.可以将数组转换为二叉树

二叉树扁平化可以转换为数组，同样二叉树也可以通过将数组转换来实现。只需要推出数组下标和二叉树对应位置的关系就可以实现数组和二叉树的转换。

实现代码如下：

 public static TreeNode  arrayToTree(List<Integer> arrayList, int index){
        //参数index表示从数组下标为index的位置开始转换
        if(arrayList.size() <= index)
            return null;
        else{
            TreeNode treeNode = new TreeNode(arrayList.get(index));
            treeNode.left = arrayToTree(arrayList, index*2+1);
            treeNode.right = arrayToTree(arrayList, index*2+2);
            return treeNode;
        }
    }

二叉树的根节点对应数组中的index下标位置，左子树节点对应index*2+1，右子树对应index*2+2，通过不断递归形成二叉树，递归出口是当index超出了数组的长度的时候，也就是下标超出了数组界限的时候。

 

二叉树最常见的遍历方式有三种，前序，中序和后序

一. 前序遍历

前序遍历就是按照根节点，左子树，右子树的顺序来遍历二叉树，在遍历左右子树的时候依然是采用前序遍历的方式

 

 

 

 

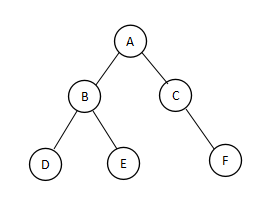
前序遍历的结果为：ABDECF

 

生成一棵这样的二叉树

 

//构建二叉树类
class TreeNode {
   
    char c;
    TreeNode left;
    TreeNode right;

    TreeNode(char c) {
        this.c = c;
    }
}

 

    TreeNode root3 = new TreeNode('A');
    root3.left = new TreeNode('B');
    root3.right = new TreeNode('C');
    root3.left.left = new TreeNode('D');
    root3.left.right = new TreeNode('E');
    root3.right.right = new TreeNode('F');

 

前序遍历递归代码

//递归方法前序遍历二叉树
    public static void preOrderRe(TreeNode node) {
        if(node == null)
            return;
        System.out.print(node.c + " ");
        preOrderRe(node.left);
        preOrderRe(node.right);
    }

前序遍历非递归栈代码

 //非递归栈实现前序遍历
    public static void preOrder(TreeNode node){
        if(node == null){
            return;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(node);
        while(!stack.isEmpty()){
            //出栈和进栈
            TreeNode n = stack.pop();//弹出根结点
            //压入子结点
            System.out.print(n.val + " ");
            if(n.right!=null){
                stack.push(n.right);

            }
            if(n.left!=null){
                stack.push(n.left);
            }
        }

    }

 

运行结果：

 

 

二. 中序遍历

中序遍历就是按照左子树，根节点，右子树的顺序来遍历二叉树，在遍历左右子树的时候依然是采用中序遍历的方式

 以上图的二叉树为例子，中序遍历的结果为：DBEACF

 //递归方法中序遍历二叉树
    public static void midOrderRe(TreeNode node) {
        if (node == null)
            return;
        midOrderRe(node.left);
        System.out.print(node.c + " ");
        midOrderRe(node.right);
    }

//非递归栈实现中序遍历
    public static void midOrder(TreeNode node){
        Stack<TreeNode> stack = new Stack<>();
        while (node != null || !stack.isEmpty()){
            while (node != null){
                stack.push(node);
                node = node.left;
            }
            if(!stack.isEmpty()){
                node = stack.pop();
                System.out.println(node.c + " ");
                node = node.right;
            }
        }

    }

运行结果：

 

 

 

 

三. 后序遍历

中序遍历就是按照左子树，右子树，根节点的顺序来遍历二叉树，在遍历左右子树的时候依然是采用后序遍历的方式

 以上图的二叉树为例子，中序遍历的结果为：DEBFAC

//递归方法后序遍历二叉树
    public static void postOrderRe(TreeNode node) {
        if (node == null)
            return;
        postOrderRe(node.left);
        postOrderRe(node.right);
        System.out.print(node.c + " ");
    }

 

 

//非递归栈实现后序遍历
    public List<Integer> postorderTraversal(TreeNode root) {
        //迭代
        List<Integer> list = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode prev = null;
        while (root != null || !stack.isEmpty()){
            while (root != null){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if(root.right == null || root.right == prev){
                list.add(root.val);//如果之前标记的出栈节点是root的右节点，说明root是时候出栈了
                prev = root;//标记出栈节点
                root = null;
            }else {
                //右节点不为空则此根节点再次入栈
                stack.push(root);
                root = root.right;//root指向右节点
            }
        }
        return list;
    }

 

 

 

运行结果：

 

 

 

四. 层序遍历

层序遍历二叉树就是从上到下，从左到右，一层一层地遍历二叉树

 以上图的二叉树为例子，层序遍历的结果为：ABCDEF

层序遍历可以通过队列来实现

 //层序遍历，使用队列，从上到下，从左到右
    public static void levelOrder(TreeNode node){
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.offer(node);
        while (!queue.isEmpty()){
            int size = queue.size();
            for (int i=0; i<size; i++){
                node = queue.poll();
                System.out.print(node.c + " ");
                if(node.left != null)
                    queue.offer(node.left);
                if(node.right != null)
                    queue.offer(node.right);
            }
            System.out.println();
        }
    }

运行结果：