从 BST 到 Splay
从 BST 到 Splay树
想必在开始学习平衡树之前一定听过许多的数据结构名称
BST (二叉排序树)、AVL 树、替罪羊树、Splay伸展树,红黑树,B树 等
当然我们首先要从 二叉排序树BST开始
而AVL树 既是 基于BST(二叉搜索树)的一种自平衡二叉搜索树,这也就是平衡部分的开始
由于在插入数值的时候,有可能使得BST退化成链的状态
那么此时在搜索时,时间复杂度则会从\(O(logn)\)退化成\(O(n)\)
所以 $G. M. Adelson-Velsky $ 和 \(E. M. Landis\) 提出算法,通过一次或者多次树旋转来尽可能平衡这棵树使得时间复杂度维持在\(O(logN)\), 即尽可能的保持完全二叉树的状态
BST (二叉排序树)
性质:
\(如果左子树不为空,则左子树上所有结点的值均小于根结点的值。\)
\(如果右子树不为空,则右子树上所有结点的值均大于根结点的值。\)
\(左、右子树也分别为二叉排序树\)
AVL
在满足 BST 的基础上:增加四种旋转操作,也就是在《数据结构》中学习的\("LL,RR,LR,RL"\)旋转
同时由于是自平衡数据结构,那么就要记录阶段的有关平衡因子,所以在编写的时候还是比较复杂的
\(LL:LeftLeft\),也称“左左”。插入或删除一个节点后,根节点的左孩子(Left Child)的左孩子(Left Child)还有非空节点,导致根节点的左子树高度比右子树高度高2,AVL树失去平衡。
\(RR:RightRight\),也称“右右”。插入或删除一个节点后,根节点的右孩子(Right Child)的右孩子(Right Child)还有非空节点,导致根节点的右子树高度比左子树高度高2,AVL树失去平衡。
\(LR:LeftRight\),也称“左右”。插入或删除一个节点后,根节点的左孩子(Left Child)的右孩子(Right Child)还有非空节点,导致根节点的左子树高度比右子树高度高2,AVL树失去平衡。
\(RL:RightLeft\),也称“右左”。插入或删除一个节点后,根节点的右孩子(Right Child)的左孩子(Left Child)还有非空节点,导致根节点的右子树高度比左子树高度高2,AVL树失去平衡
可以理解为 “xx” 位置失重的调整
可以参考下这篇博客对AVL树旋转操作详解:https://www.cnblogs.com/cherryljr/p/6669489.html
而如果对于一些数据更改频繁,反而查找那么频繁的,AVL树在插入删除更改时,导致的大量时间消耗反而不划算
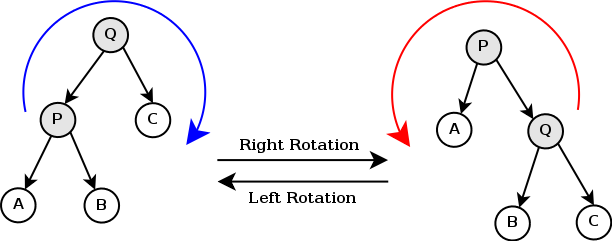
\(图片来自wiki\)
这里推荐一个比较好的网站:https://csacademy.com/app/graph_editor/ 可以自己试着模拟旋转以下
//right右旋为1,left左旋为0
void rotate(ll x,int op){
//1)找父亲
ll y = f[x], z = f[y];
//ch[x][] 表示左0,右1儿子结点
//2)右旋右挂左,左旋左挂右
ch[y][op^1] = ch[x][op];
if(!ch[x][op]) f[ch[x][op]] = y;
f[x] = z,f[y] = x;
//如果祖先结点存在,根据y为z的左右孩子位置,用于x来替换
if(!z) ch[z][ch[z][1]==y] = x;
ch[x][op] = y;
}
Splay
在了解splay之前还是来看看关于二叉树常见的问题:
动态插入数字,并询问第 \(Kth\) 。
对于普通的二叉树而言,我们只要维护一个左右子树中结点的个数即可。但是常见的问题还是在于:如果为单增的序列则会退化为链的问题。
相比\(AVL树\) 记录平衡因子(尽可能保证绝对平衡)而言,\(splay\)只需要保证相对的平衡就行了。\(splay\) 的操作是每次插入后将其进行旋转,一直转到根结点位置。这样就可以在旋转中减少 退化而引起的问题。同时将每次找到的值向根节点旋转也有助于频繁访问的结点快速被找到。
所以可以理解为
splay(x) = while(f[x]!=root) rotate(x);
然后就是对应的各种旋转情况
$Zig-Zig $

当p不是根节点,且x和p同为左孩子或右孩子时进行Zig-Zig操作。
当x和p同为左孩子时,依次将p和x右旋;
当x和p同为右孩子时,依次将p和x左旋。
\(Zig - Zag\)
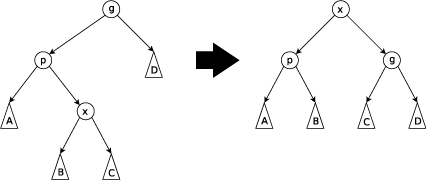
当p不是根节点,且x和p不同为左孩子或右孩子时,进行Zig-Zag操作。
当p为左孩子,x为右孩子时,将x左旋后再右旋。
当p为右孩子,x为左孩子时,将x右旋后再左旋。
参考博客 https://blog.csdn.net/changtao381/article/details/8936765
void splay(ll x,ll root){
while(f[x]!=root){
ll y = f[x],z = f[y];
//单旋情况
if(z == root){
if(ch[y][1] == x) rotate(x,0);//x为右子则左旋
else rotate(x,1);//否则右旋
}
//双旋情况
else{
if(ch[z][0] == y){
if(ch[y][0] == x) rotate(y,1), rotate(x,1); // LL
else rotate(x,0), rotate(x,1);//LR
}else{
if(ch[y][1] == x) rotate(y,0), rotate(x,0);//RR
else rotate(x,1), rotate(x,0);//RL
}
}
}
}
查找find操作
从根节点开始,左侧都比他小,右侧都比他大,相对递归即可 \(w[u]记录结点值\)
void find(ll x){
ll u = root;
if(!u) return;//空树
while(ch[u][x > w[u]] && x != w[u])//当存在儿子并且当前位置的值不等于x
u = ch[u][x > w[u]];
splay(u,0);//将找到的 x 向上旋转
}
插入操作
类似find操作,如果已经存在则直接在查找的结点计数,否则新建结点
void insert(ll x){
ll u = root,fu = 0;
//u存在且没有查找到x
while(u && w[u] != x){
fu = u;
u = ch[u][x > w[u]];
}
if(u) num[u]++;//则增加一个这样的数
else{
u = ++tot;//新增结点
//父节点非根
if(fu) ch[fu][x > w[fu]] = u;
ch[u][0] = ch[u][1] = 0;//不存在儿子
f[tot] = fu;//父节点
w[tot] = x;//结点值
num[tot] = 1;//含有此数的个数
siz[tot] = 1;//含有不同个数值
}
splay(u,0);//旋转并保证结构平衡
}
前驱/后继
查找前驱既是在左子树上找到最大的值,后继则反过来即可
ll get_nex(ll x,ll nx){
find(x);
ll u = root;//根节点
if(w[u] > x && nx) return u;//如果当前节点的值大于x并且要查找的是后继
if(w[u] < x && !nx) return u;
u = ch[u][nx]; //查找后继的话在右儿子上找,前驱在左儿子上找
while(ch[u][nx^1]) u = ch[u][nx^1];//要反着跳转,否则会越来越大(越来越小)
return u;
}
删除操作
首先找到这个数的前驱,然后splay到根结点,然后找到后继旋转到前驱的下面
比前驱大的数是后继,在右子树. 比后继小的且比前驱大的有且仅有当前数在后继的左子树上面
因此直接将当前节点的右儿子的左儿子删除即可
void delete(ll x){
ll las = get_nex(x,0);
ll nex = get_nex(x,1);
splay(las,0),splay(nex,las);
ll del = ch[nex][0];
//删除值个数超过1个
if( num[del] > 1){
num[del]--;
splay(del,0);
}else{
ch[nex][0] = 0;//此节点直接删除
}
}
查询第K大
和权值线段树差不多,都是二叉树节点记录权值信息
通过比较大小和个数即可
ll kth(ll x){
ll u = root;
//如果树上没有这么多的数
if(size[u] < x) return 0;
while(1){
ll y= ch[u][0];//左儿子
if(x>size[y]+num[u])
//如果排名比左儿子的大小和当前节点的数量要大
{
x-=size[y]+num[u];//数量减少
u= ch[u][1];//那么当前排名的数一定在右儿子上找
}
else//否则的话在当前节点或者左儿子上查找
if(size[y]>=x)//左儿子的节点数足够
u=y;//在左儿子上继续找
else//否则就是在当前根节点上
return w[u];
}
}
接下来就是模板总结了
个人模板:
struct Splay
{
#define maxn (int)1e5+5
//个数,大小,权值
int num[maxn],siz[maxn]; ll w[maxn];
//父亲,孩子
int f[maxn],ch[maxn][2];
// 下标,根节点
int tot,root;
void splay(int x,int root){
while(f[x]!=root){
int y = f[x],z = f[y];
//单旋情况
if(z == root){
if(ch[y][1] == x) rotate(x,0);//x为右子则左旋
else rotate(x,1);//否则右旋
}
//双旋情况
else{
if(ch[z][0] == y){
if(ch[y][0] == x) rotate(y,1), rotate(x,1); // LL
else rotate(x,0), rotate(x,1);//LR
}else{
if(ch[y][1] == x) rotate(y,0), rotate(x,0);//RR
else rotate(x,1), rotate(x,0);//RL
}
}
}
}
void find(int x){
int u = root;
if(!u) return;//空树
while(ch[u][x > w[u]] && x != w[u])//当存在儿子并且当前位置的值不等于x
u = ch[u][x > w[u]];
splay(u,0);//将找到的 x 向上旋转
}
void insert(int x){
int u = root,fu = 0;
//u存在且没有查找到x
while(u && w[u] != x){
fu = u;
u = ch[u][x > w[u]];
}
if(u) num[u]++;//则增加一个这样的数
else{
u = ++tot;//新增结点
//父节点非根
if(fu) ch[fu][x > w[fu]] = u;
ch[u][0] = ch[u][1] = 0;//不存在儿子
f[tot] = fu;//父节点
w[tot] = x;//结点值
num[tot] = 1;//含有此数的个数
siz[tot] = 1;//含有不同个数值
}
splay(u,0);//旋转并保证结构平衡
}
int get_nex(int x,int nx){
find(x);
int u = root;//根节点
if(w[u] > x && nx) return u;//如果当前节点的值大于x并且要查找的是后继
if(w[u] < x && !nx) return u;
u = ch[u][nx]; //查找后继的话在右儿子上找,前驱在左儿子上找
while(ch[u][nx^1]) u = ch[u][nx^1];//要反着跳转,否则会越来越大(越来越小)
return u;
}
void delete(int x){
int las = get_nex(x,0);
int nex = get_nex(x,1);
splay(las,0),splay(nex,las);
int del = ch[nex][0];
//删除值个数超过1个
if( num[del] > 1){
num[del]--;
splay(del,0);
}else{
ch[nex][0] = 0;//此节点直接删除
}
}
ll kth(int x){
int u = root;
//如果树上没有这么多的数
if(size[u] < x) return 0;
while(1){
int y= ch[u][0];//左儿子
if(x>size[y]+num[u])
//如果排名比左儿子的大小和当前节点的数量要大
{
x-=size[y]+num[u];//数量减少
u= ch[u][1];//那么当前排名的数一定在右儿子上找
}
else{
//否则的话在当前节点或者左儿子上查找
//左儿子的节点数足够
if(size[y]>=x){
u=y;//在左儿子上继续找
}
else{
//否则就是在当前根节点上
return w[u];
}
}
}
}
}splay;


