HDU - 1045 Fire Net （dfs 或 二分图）

题意：给出一个不会超过4x4的map
map中有墙，以及空白处。然后你要在空白处放置尽可能多的炮台
炮台对向四周发射子弹，即（炮台不能放在同一行或者列除非有墙阻挡）
思路：首先想到了dfs枚举（就像八皇后一样回溯法），我们尽可能多的在
一行一行的放置.关于放置搜索的问题，我们判断是否合法
关于二分图匹配(完全没有想出来怎么匹配..)在网上看了别人的题解才懂
由于同行或者同列不能多个放置(即每行每列只能放一个除了有墙挡)
然后就是建图:将每行每列连续的部分缩成一个点
如图：（不要纠结线条是不是直的啦

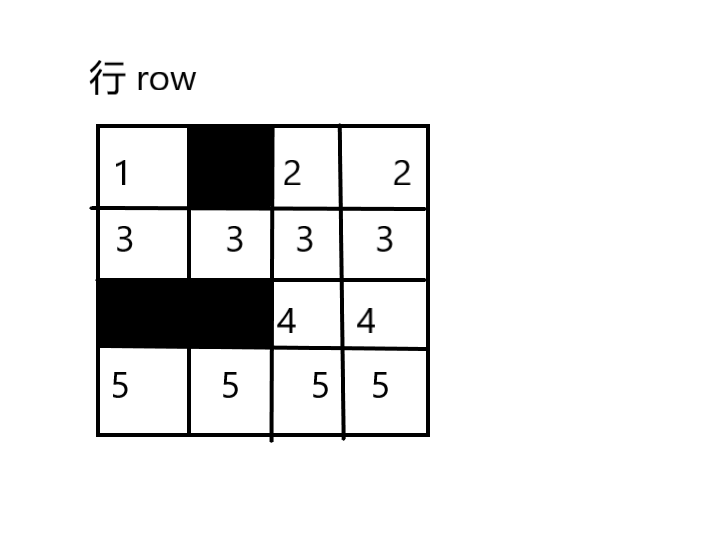
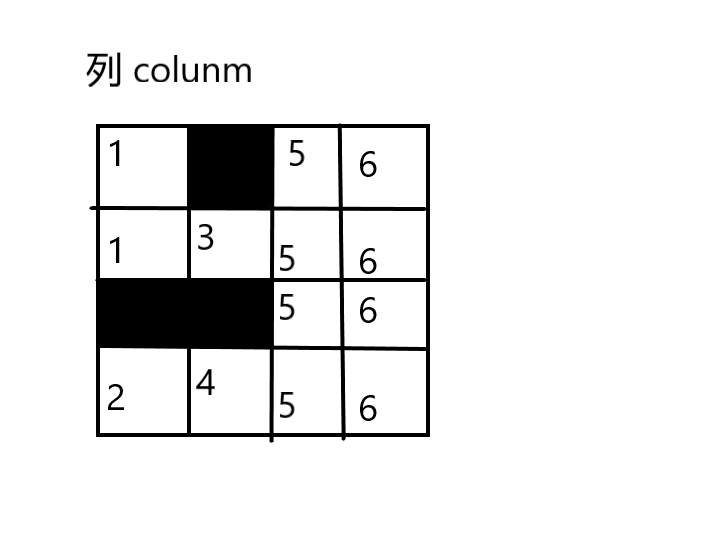
我们然后这就有连接关系。假设i为行号，j为列号。ij有一条边，即是图中放了一个(i,j)点
比如在第一行我们可以选择 (1,3)或(1,4)或(1,5)
最大匹配正好是满足连接关系的最大数目，所以用匈牙利算法即可求

二分图代码：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
char G[5][5];
int map[20][20],col[5][5],row[5][5];
int match[20],vis[20]; 
int cntx ,cnty,n;
bool Find(int u){
    for(int i=0; i<cnty; i++){
        int x = i;
        if(!vis[x] && map[u][x]){
            vis[x] = 1;
            if(!match[x] || Find(match[x])){
                match[x] = u;
                return true;
            }
        }
    }
    return false;
}
void init(){
    memset(G,0,sizeof(G));
    memset(col,0,sizeof(col));
    memset(row,0,sizeof(row));
    memset(map,0,sizeof(map));
}
int main(){
    while(cin>>n&&n){
        init();
        //从(0,0)开始存图 
        for(int i =0;i<n;i++){
            scanf("%s",&G[i]);
        }
        //建图 
        cntx= cnty = 1;
        for(int i = 0;i < n;i++){
            for(int j = 0;j < n;j++){
                if(G[i][j] == '.') row[i][j] = cntx;
                else cntx++;
                if(G[j][i]=='.') col[j][i] = cnty;
                else cnty++;
            }
            cntx++;
            cnty++;
        }
 
        //连接 
        for(int i =0 ;i<n;i++){
            for(int j =0;j<n;j++){
                if(G[i][j]=='.') map[row[i][j]][col[i][j]] = 1;
            }
        }
        int ans = 0;
        memset(match,0,sizeof(match));
        for(int i=0;i<cntx;i++){
            memset(vis,0,sizeof(vis));
            if(Find(i)) ans++;
        }
        cout<<ans<<endl;
    }
}

 

dfs代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
char G[5][5];//记录地图
int hav[5][5];//记录炮台是否存在
int n;
int ans;
bool check(int x,int y) {
    //由于是增行的，所以往前面寻找是否有墙或者炮台
    for(int i = x; i>=1; i--) {
        if(G[i][y] == 'X') break;
        if(hav[i][y] == 1) return 0;
    }
    //往改行之前的列搜索
    for(int i = y; i>=1; i--) {
        if(G[x][i] == 'X') break;
        if(hav[x][i] == 1) return 0;
    }
    return 1;
}
void dfs(int x,int y,int cur) {
    //放置边界
    if(x == n && y == n){
        if(G[x][y] == '.' &&check(x,y)) cur++;
        ans = max(ans,cur);
        return ;
    }
    //到每行尾，搜索下一行
    if(y == n) {
        if(G[x][y] == '.' && check(x,y)) {
            hav[x][y]=1;
            dfs(x+1,1,cur+1);
            //回溯
            hav[x][y]=0;
        }
        dfs(x+1,1,cur);
    }
    else {
        if(G[x][y] == '.' && check(x,y)) {
            hav[x][y]=1;
            dfs(x,y+1,cur+1);
            hav[x][y]=0;
        }
        dfs(x,y+1,cur);
    }
    
}
int main(){
    while(cin>>n&&n){
        ans = 0;
        memset(hav,0,sizeof(hav));
        for(int i= 1;i<=n;i++){
            scanf("%s",G[i]+1);
        }
        dfs(1,1,0);
        cout<<ans<<endl;
    }
}