20220317 刷题日记

P7514

把昨天空闲时候想出来的卡牌游戏写了。有一点不优美的地方是关注到所有的上界是所有出现过的数，而不是 \(a\) 数组中的数，这个坎导致我的思路走了一些小小的弯路。

CF1017G

如果忽略 2 操作，等价于询问一个点到根路径上是否存在一个后缀使得这一条后缀上的操作次数和大于等于深度之差。

考虑到关于深度，一个常见的思路是每个点都初始为 1 或 -1 来吧深度之差干掉。

这里每个点初始为 -1，这样就等价于询问一条最大后缀满足和为 \(0\)。

然后考虑 \(2\) 操作，首先等价于子树清空，然后考虑如果询问该子树的最大后缀，可能还是会有问题，因为上面的信息可能传下来，我们只需要在根节点上进行对应的相减即可。

P4748

如果 \(k\) 是答案，一个必要条件是 \(k+1|n\)，我们考虑这样每一个连通块的大小我们是能够知道的。

考虑一条边会被割，必要条件是割完这条边，两个连通块的大小必须都是我们已经算出的那个连通块大小的倍数。

考虑满足上面的条件的边一共有几条，考虑如果一个 \(k\) 是答案的话，上面的边一定恰好有 \(k\) 条，否则一定不足 \(k\) 条，可以通过反证法证明不可能超过 \(k\) 条。

于是处理出来子树大小即可。由于 \(10^6\) 以内的因子个数最多有 \(240\) 个，所以可以暴力枚举。

P7880

思路具有极大的启发式意义。

首先考虑数颜色问题，序列上的话我们只需要考虑最后一次出现的位置。书上也是一样，考虑到 lca 其实只有 \(O(n)\) 个，对于三个点对 \((b,c)(a,c)\) 如果他们的 \(lca\) 一样的，且满足 \(a<b<c\)，那么我们可以看到如果一个区间可以包含 \((a,c)\)，那么一定可以包含 \((b,c)\)，所以 \((a,c)\) 是无用的。

这是一个很关键的点，因为这样有效降低了我们的点对数量。现在点对变成了一个点，在其他的子树内的前驱后继。我们考虑这样的点对数仍然很多。

我们考虑启发式合并的做法，每次把小字树合并到大子树里，顺便维护小子树内的每个点在大子树内的前驱后继，这样的话我们的点数就和启发式合并的合并次数一样了，为 \(O(n\log n)\)，由于查前驱后继有 set，所以是两个 \(\log\)。

考虑一个点对 \((a,b)\) 表示当 \(1\le l\le a,b\le r\le n\) 的时候会出现这个颜色。把这个东西映射到二维平面上，然后发现是这样的一个结构：

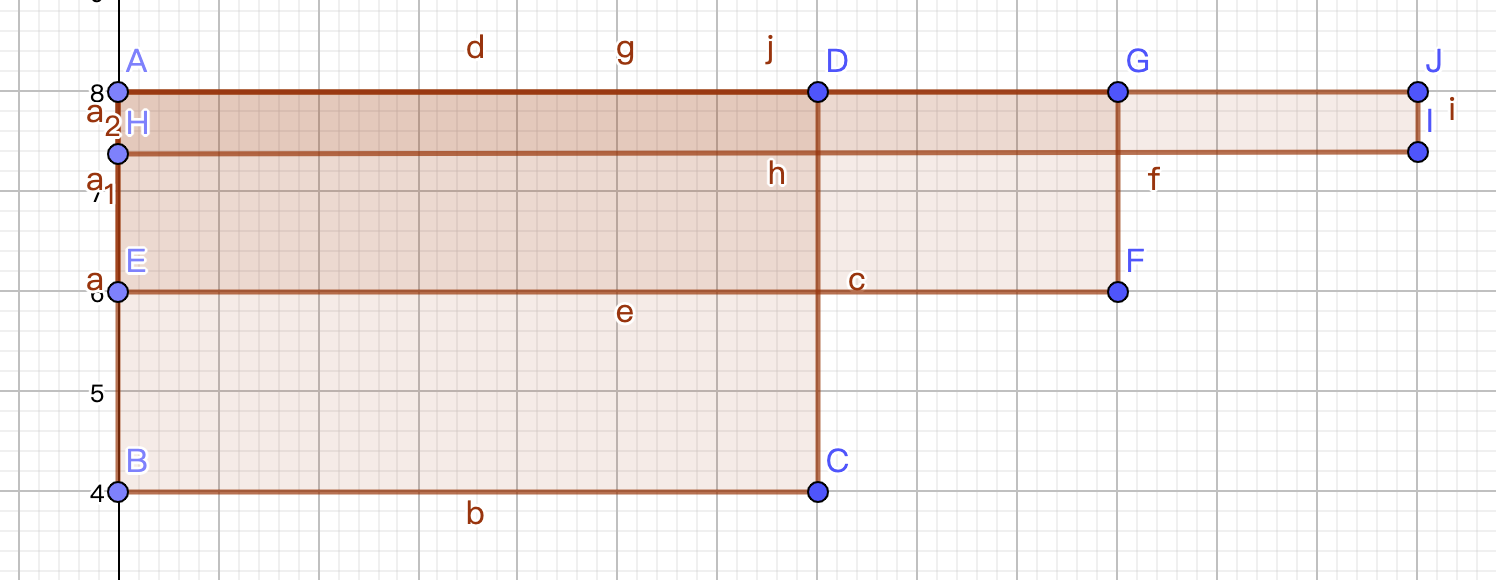
图有问题的一点是，需要保证 \((a,b)\) 中的 \(a<b\)，不过小问题。小于的原因是这里表示的是关于范围的限制。

那么我们想要做的其实是对每个颜色，所有这样的矩形做一个面积并，然后把面积并加一，这样单点查就可以做完了。

但实际上就是这里罚坐了两个小时。

我们考虑从左往右扫，不好做，为什么？因为这个东西是从高到低的。

但是从下往上扫是从低到高的。

所以我们考虑从下往上扫，维护每个颜色的当前高度，及时更新，加入一个颜色的时候，要先删掉，然后再加上这时的最大值带来的影响，因为是前缀，所以用树状数组即可。