平衡树入门——FHQ_Treap

平衡树入门——FHQ_Treap

1 简介

FHQ treap，也有人称之为无旋 Treap，因为没有旋转，所以可以支持可持久化，也可以支持序列操作，常数略大，速度比 Splay 快。用两个操作——插入和删除就完成了对整个 Treap 的维护。自我感觉代码复杂度比 Treap，Splay 很低。容易理解，理解后记忆代码十分容易。

2 数据结构解析

2.1 节点信息

FHQ Treap 和 Treap 的节点信息是一样的——除了一点以外：

struct node{
    int val,size,key,l,r;
};
node p[N];

相信读者已经发现了，FHQ Treap 没有记录相同权值节点的个数，也就是说，就算有相同权值的节点，也不能够把这些节点当做一个节点来处理。这带来了一定意义上空间的浪费，不过少维护一些东西可以让编程复杂度降低。

这里 \(val\) 是权值，\(size\) 是子树大小，\(key\) 是 Treap 的随机值，\(l,r\) 分别是左右儿子。

2.2 创造新节点

    inline int new_node(int val){
        p[++tot].val=val;p[tot].key=random(INF);
        p[tot].l=p[tot].r=0;p[tot].size=1;
        return tot;
    }

其中：

inline int random(int n){
    return rand()*rand()%n+1;
}

这里 \(tot\) 是节点总量，\(val\) 是所插入节点的权值。这段代码不作讲解。

2.3 合并信息

    inline void pushup(int k){
        p[k].size=p[p[k].l].size+p[p[k].r].size+1;
    }

太过于简单，不作讲解。

2.4 分裂

inline void split(int k,int val,int &x,int &y){//depend on val
    if(k==0){
        x=y=0;return;
    }
    if(p[k].val<=val){
        x=k;
        split(p[k].r,val,p[k].r,y);
    }
    else{
        y=k;
        split(p[k].l,val,x,p[k].l);
    }
    pushup(k);
}

使用 split(k,val_,x,y) 就相当于完成了这样一件事情：把以 \(k\) 为根的子树按照权值分裂，其中权值小于等于 val_ 的最终会到以 \(x\) 为根的树中，大于 val_ 的权值会到以 \(y\) 为根的树中。注意到 \(x\) 和 \(y\) 是通过引用传回来的。

我们现在重点关注一下他是如何分裂的，首先，如果 \(k=0\) 那么这就代表已经分裂结束或者这颗树为空，不管是哪一种情况，这个时候，让引用的 \(x,y\) 等于 \(0\) 是不影响结果的，因为这个时候并没有那一颗子树被分到了以 \(x\) 为根或以 \(y\) 为根的子树上去。

否则，如果这个节点的权值是小于等于 \(val\) 的，说明 \(k\) 这个节点和 \(k\) 这个节点的左子树都会被划分到 \(x\) 这颗子树上去，而此时此刻，\(k\) 这个节点的右子树还没有被划分，所以我们在去划分一下 \(k\) 的右子树，注意我们是带引用的去进行递归的，所以如果有要划分到 \(x\) 这个子树上的节点，我们就把它挂到右子树上去，这也是为什么我们把第三个参数变为 p[k].r 。第 \(9\) 到第 \(12\) 行同理。

这里的引用有效降低了编程复杂度。

当然我们依然可以使用大小进行分裂，通常来说，根据题目不同的要求，两种分裂方式都是必须要掌握的。整体思路和按照权值分裂一样。

inline void split(int k,int siz,int &x,int &y){
    if(!k){x=0;y=0;return;}
    if(p[p[k].l].size+1<=siz){
        x=k;split(p[k].r,siz-p[p[k].l].size-1,p[x].r,y);PushUp(x);
    }
    else{y=k;split(p[k].l,siz,x,p[y].l);PushUp(y);}
}

2.5 合并

    inline int merge(int x,int y){
        if(x==0||y==0) return x+y;
        if(p[x].key>p[y].key){
            p[x].r=merge(p[x].r,y);
            pushup(x);
            return x;
        }
        else{
            p[y].l=merge(x,p[y].l);
            pushup(y);
            return y;
        }
    }

这一段代码完成的是把以 \(x\) 为根的子树与以 \(y\) 为根的子树合并，注意这里保证以 \(x\) 为根的子树的权值最大值要小于以 \(y\) 为根的子树的权值最小值。注意这里我们需要维护优先级。因为有上面那个性质，所以我们不用判断节点权值大小而可以直接合并，最后这段代码传回的是合并完两颗子树后的根节点。

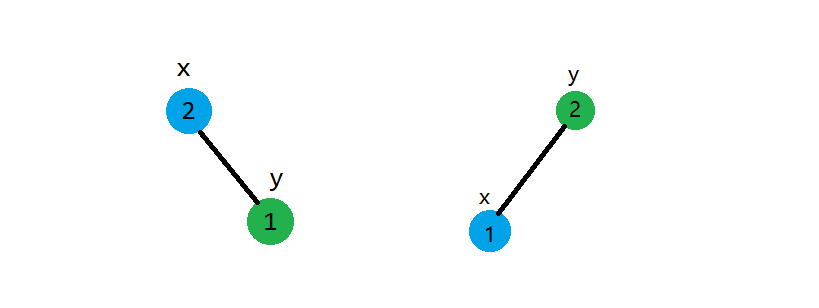
不难理解这段代码：如果 \(x\) 的优先值大于 \(y\) 的优先值，如图：

不难发现的是，\(x\) 的左子树就不需要进行合并的，需要在进行合并的是 \(x\) 的右子树和 \(y\) 这颗子树，递归进行就可以。\(y\) 的优先级更大是同理的。如果其中一颗子树为空，那么我们直接返回 \(x+y\) 就可以，如果另一颗子树不为空那么返回的就是另一颗子树的根节点，如果两颗子树都为空也不失正确性。

2.6 插入

其实有了上面这两个操作其它操作的实现就非常简单了。

    inline void insert(int val){
        int x,y;
        split(root,val-1,x,y);
        root=merge(merge(x,new_node(val)),y);
    }

这个函数能够往平衡树中插入一个权值为 \(val\) 的节点。

如何实现的呢？我们按照权值 \(val-1\) 来进行分裂，分裂之后，权值小于等于 \(val-1\) 的节点都在以 \(x\) 为根的子树中，其他节点在以 \(y\) 为根的子树中，然后我们先把 \(x\) 与我们新建的节点合并，然后再合并整棵树。

2.7 删除

    inline void delete_(int val){
        int x,y,z;
        split(root,val,x,z);
        split(x,val-1,x,y);
        if(y){
            y=merge(p[y].l,p[y].r);
        }
        root=merge(merge(x,y),z);
    }

不难发现在分裂之后，以 \(y\) 为根的子树里只有权值等于 \(val\) 的节点，我们合并左右子树——删除根就可以。

如果要删除所有权值为 \(val\) 的节点，就不用写第 \(6\) 到第 \(9\) 行。

删完之后，我们把整棵树重新合并。

2.8 查询排名

inline int getrank(int val){
    int x,y,ans;
    split(root,val-1,x,y);
    ans=p[x].size+1;
    root=merge(x,y);
    return ans;
}

某个数的排名就是比他小的数的个数 \(+1\) ，所以不难理解上面这个代码。

2.9 查询值

inline int getval(int rank){
    int k=root;
    while(k){
        if(p[p[k].l].size+1==rank) break;
        else if(p[p[k].l].size>=rank) k=p[k].l;
        else rank-=p[p[k].l].size+1,k=p[k].r;
    }
    return k==0?INF:p[k].val;
}

这个和普通的平衡树查询值是一样的，不作讲解。

2.10 查询前驱后继

inline int getpre(int val){
    int x,y,k,ans;
    split(root,val-1,x,y);
    k=x;
    while(p[k].r) k=p[k].r;
    ans=p[k].val;
    root=merge(x,y);
    return ans;
}
inline int getnext(int val){
    int x,y,k,ans;
    split(root,val,x,y);
    k=y;while(p[k].l) k=p[k].l;
    ans=p[k].val;
    root=merge(x,y);
    return ans;
}

如果要查询前驱，我们就按照 \(val-1\) 分裂整颗树，然后取 \(x\) 子树最靠右的节点就可以了，查询后继同理。

2.11 优化

因为在一定程度上 FHQ Treap 有点浪费空间，所以我们可以开一个栈，把所以删除的节点编号存一下，然后插入新节点时我们优先使用这些被删除的节点。代码就看这篇博客，同时这篇博客还讲解了如何判断某一个节点是否存在，以及返回整颗输的大小等操作，相信有了分裂和合并，这些操作不难实现。

3 总代码

#include<bits/stdc++.h>
#include<cstdlib>
#define dd double
#define ld long double
#define ll long long
#define uint unsigned int
#define ull unsigned long long
#define N 500100
#define M number
using namespace std;

const int INF=0x3f3f3f3f;

template<typename T>  inline void read(T &x) {
    x=0; int f=1;
    char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c == '-') f=-f;
    for(;isdigit(c);c=getchar()) x=x*10+c-'0';
    x*=f;
}

struct node{
    int val,size,key,l,r;
};
node p[N];

inline int random(int n){
    return rand()*rand()%n+1;
}

struct FHQ_Treap{
    int tot,root;
    inline void pushup(int k){
        p[k].size=p[p[k].l].size+p[p[k].r].size+1;
    }
    inline int new_node(int val){
        p[++tot].val=val;p[tot].key=random(INF);
        p[tot].l=p[tot].r=0;p[tot].size=1;
        return tot;
    }
    inline void split(int k,int val,int &x,int &y){//depend on val
        if(k==0){
            x=y=0;return;
        }
        if(p[k].val<=val){
            x=k;
            split(p[k].r,val,p[k].r,y);
        }
        else{
            y=k;
            split(p[k].l,val,x,p[k].l);
        }
        pushup(k);
    }
    inline int merge(int x,int y){
        if(x==0||y==0) return x+y;
        if(p[x].key>p[y].key){
            p[x].r=merge(p[x].r,y);
            pushup(x);
            return x;
        }
        else{
            p[y].l=merge(x,p[y].l);
            pushup(y);
            return y;
        }
    }
    inline void insert(int val){
        int x,y;
        split(root,val-1,x,y);
        root=merge(merge(x,new_node(val)),y);
    }
    inline void delete_(int val){
        int x,y,z;
        split(root,val,x,z);
        split(x,val-1,x,y);
        if(y){
            y=merge(p[y].l,p[y].r);
        }
        root=merge(merge(x,y),z);
    }
    inline int getrank(int val){
        int x,y,ans;
        split(root,val-1,x,y);
        ans=p[x].size+1;
        root=merge(x,y);
        return ans;
    }
    inline int getval(int rank){
        int k=root;
        while(k){
            if(p[p[k].l].size+1==rank) break;
            else if(p[p[k].l].size>=rank) k=p[k].l;
            else rank-=p[p[k].l].size+1,k=p[k].r;
        }
        return k==0?INF:p[k].val;
    }
    inline int getpre(int val){
        int x,y,k,ans;
        split(root,val-1,x,y);
        k=x;
        while(p[k].r) k=p[k].r;
        ans=p[k].val;
        root=merge(x,y);
        return ans;
    }
    inline int getnext(int val){
        int x,y,k,ans;
        split(root,val,x,y);
        k=y;while(p[k].l) k=p[k].l;
        ans=p[k].val;
        root=merge(x,y);
        return ans;
    }
};
FHQ_Treap treap;

int n;

int main(){
//    freopen("my.out","w",stdout);
    read(n);
    for(int i=1;i<=n;i++){
        int op,x;read(op);read(x);
        if(op==1) treap.insert(x);
        else if(op==2) treap.delete_(x);
        else if(op==3) printf("%d\n",treap.getrank(x));
        else if(op==4) printf("%d\n",treap.getval(x));
        else if(op==5) printf("%d\n",treap.getpre(x));
        else if(op==6) printf("%d\n",treap.getnext(x));
    }
    return 0;
}

引用

• ctjcalc的博客

当你想要结束的时候，想想你为什么开始！